
- •Куцый н. Н. Системы искусственного интеллекта
- •1.Искусственный интеллект
- •2.Агенты – носители искусственного интеллекта
- •3. Среды и агенты
- •4.Логические рассуждения
- •5.Логика высказываний
- •6.Исчисление высказываний
- •7.Рассуждения в терминах интервалов
- •9.Логика предикатов
- •9.Постановка задачи для среды чудовища в логике предикатов.
- •10.Исчисление предикатов
- •11.Прямой и обратный вывод
- •12.Полнота и непротиворечивость исчисления
- •13.Вывод на основе правила резолюции
- •14.Автомат и среда
- •15.Язык и автомат
- •Вопросы и упражнения
13.Вывод на основе правила резолюции
Правило резолюции (или резолюция) уже рассматривалось. это правило гласит, что из истинности двух дизъюнкций, одна из которых содержит дизъюнкт, а другая – его отрицание, следует (выводима) формула, которая является дизъюнкцией исходных формул без упомянутого дизъюнкта и его отрицания. Резолюция записывалась в следующем виде:
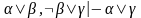 или
эквивалентно
или
эквивалентно
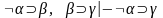 .
.
В
логике предикатов первого порядка она
выглядит так же. Формулы
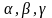 в ней являются формулами этой логики.
Введем по аналогии с обощенным правилом
модус поненс обобщенное правило
резолюции, или обобщённую
резолюцию:
в ней являются формулами этой логики.
Введем по аналогии с обощенным правилом
модус поненс обобщенное правило
резолюции, или обобщённую
резолюцию:
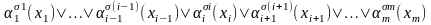 ,
,
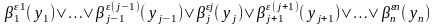 ,
,
 Унификация
Унификация
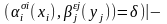
Подстановка
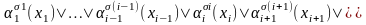
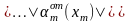
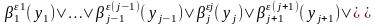
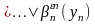 .
.
Здесь
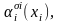
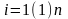 обозначается литерал, такой, что
обозначается литерал, такой, что
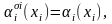 при
при
 и
и
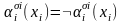 при
при
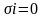 .
Аналогичный смысл имеет символ
.
Аналогичный смысл имеет символ
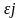 в литерале
в литерале
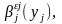
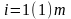 .
Подстановка
.
Подстановка
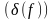 означает
формулу, которая получает из формулы
означает
формулу, которая получает из формулы
 в результате
подстановки
во все её атомы. Суть обобщенного правила
модус поненс можно ыразить следующим
образом. Если существует истинная
формула
в результате
подстановки
во все её атомы. Суть обобщенного правила
модус поненс можно ыразить следующим
образом. Если существует истинная
формула
,
которая является дизъюнкцией литералов , и истинная формула
,
которая
также является дизъюнкцией литералов
,
и в этих формулах предикатные символы
литералов
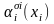 и
и
 одинаковы
одинаковы
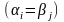 ,
,
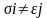 ,
и для атомов
и
существует унификация
,
которая делает их (записывается как
Унификация
,
и для атомов
и
существует унификация
,
которая делает их (записывается как
Унификация
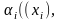
 ,
то можно вывести истинную формулу,
которая получается в результате
подстановки
в дизъюнцию исходных формул после
удаления в них литералов
и
.
Выведенную таким образом истинную
формулу называют резольвентой.
Так же как и
в случае резолюции для логики высказываний,
обобщенную резолюцию можно выразить с
использованием импликации. Обратим
внимание, что исходные формулы в
обобщенной резолюции и резольвента
являются дизъюнкцией литералов. Обычно
такие формулы называют клаузальными
формами,
или клаузами.
Таким образом, использование резолюции
для вывода требует клаузальной формы
представления знаний. Это, в свою очередь,
означает, что база знаний, вывод для
которой осуществляется на основе
обобщенной резолюции, должна представлять
собой совокупность клауз, понимаемых
в целом как формула, которая является
конъюнкцией клауз. Формулы такого типа
обычно называют конъюнктивными
нормальными формулами.
,
то можно вывести истинную формулу,
которая получается в результате
подстановки
в дизъюнцию исходных формул после
удаления в них литералов
и
.
Выведенную таким образом истинную
формулу называют резольвентой.
Так же как и
в случае резолюции для логики высказываний,
обобщенную резолюцию можно выразить с
использованием импликации. Обратим
внимание, что исходные формулы в
обобщенной резолюции и резольвента
являются дизъюнкцией литералов. Обычно
такие формулы называют клаузальными
формами,
или клаузами.
Таким образом, использование резолюции
для вывода требует клаузальной формы
представления знаний. Это, в свою очередь,
означает, что база знаний, вывод для
которой осуществляется на основе
обобщенной резолюции, должна представлять
собой совокупность клауз, понимаемых
в целом как формула, которая является
конъюнкцией клауз. Формулы такого типа
обычно называют конъюнктивными
нормальными формулами.
Прямой
вывод на основе резолюции.
Вернёмся теперь к примеру с кубиками и
повторим прямой вывод той же целевой
формулы, но уже используя обобщенную
резолюцию. Заметим, что формулы (11.1),
(11.4) уже являются клаузами. остальные
формулы с помощью простейших преобразований
на оснвое закона
 легко
преобразуются в клаузы. В результате
вместо (11.5)-(11.10) получим следующие
формулы.
легко
преобразуются в клаузы. В результате
вместо (11.5)-(11.10) получим следующие
формулы.
Формулы, которые определяют условия выполнения действий.
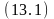 на
свободен
переместить
,
Стол
,
на
свободен
переместить
,
Стол
,
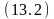 на
,
Стол
свободен
свободен
на
,
Стол
свободен
свободен
переместить .
Формулы, определяющие условия переходов состояний среды:
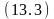 на
свободен
переместить
,Стол
на
свободен
переместить
,Стол
на , Стол ,
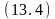 на
свободен
переместить
,Стол
на
свободен
переместить
,Стол
свободен ,
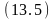 на
свободен
свободен
на
свободен
свободен
переместить на ,
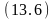 на
свободен
свободен
на
свободен
свободен
переместить свободен .
Целевая формула. Целевая формула в соответствии с рис. 11.1 является конъюнкцией литералов и при прямом выводе, как и в случае использования обобщенного правила модус поненс, будет выводится для каждого литерала, входящего в её состав, раздельно
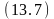 на
(A,B)
на (B,
Стол)
на (С,
Стол)
на (D,
Стол)
.
на
(A,B)
на (B,
Стол)
на (С,
Стол)
на (D,
Стол)
.
Вывод. Используя унифицированные клаузы (11.1), (13.1), которые после унификации првращаются в клаузы (13.8), (13.9) получаем резольвенту (13.10):
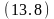 на
(A,С),
на
(A,С),
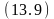 на
(A,С)
свободен (A)
переместить
(A,
Стол),
на
(A,С)
свободен (A)
переместить
(A,
Стол),
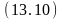 свободен
(A)
переместить
(A,
Стол).
свободен
(A)
переместить
(A,
Стол).
Используя клаузы (11.3), (13.10), получаем резольвенту
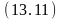 переместить
(A,
Стол).
переместить
(A,
Стол).
Используя эту резольвенту и унифицированную клаузу (13.4), которая после унификации превратилась в клаузу (13.12), получаем резольвенту (13.13):
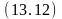 на
(A,y)
свободен (A)
переместить
(A,
Стол)
на
(A,y)
свободен (A)
переместить
(A,
Стол)
свободен (y),
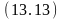 на
(A,y)
свободен (A)
свободен (y).
на
(A,y)
свободен (A)
свободен (y).
Затем, используя клаузы (11.1), (11.3) и унифицированный резольвент (13.13), получаем резольвенту
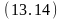 свободен
(C).
свободен
(C).
Аналогично можем получить следующие резольвенты:
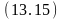 на
(A,
Стол),
на
(A,
Стол),
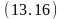 переместить
(D,
Стол),
переместить
(D,
Стол),
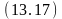 свободен
(B),
свободен
(B),
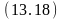 на
(D,
Стол).
на
(D,
Стол).
Итак, кубики A и D могут быть перемещены на стол, в результате чего кубики B и C окажутся свободными. После этого, используя клаузы (11.5), (11.6), (13.15) и клаузу (13.2), которая после унификации превращается в клаузу (13.19), получаем резольвенту (13.20)
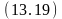 на
(A,
Стол)
свободен (A)
свободен (B)
на
(A,
Стол)
свободен (A)
свободен (B)
переместить (A,B),
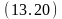 переместить
(A,B).
переместить
(A,B).
Наконец, воспользовавшись клаузами (11.5), (11.6), (13.15), (13.20) и клаузой (13.5), которая после унификации превращается в клаузу (13.21), получим резольвенту (13.22):
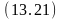 на
(A,
Стол)
свободен (A)
свободен (B)
на
(A,
Стол)
свободен (A)
свободен (B)
переместить (A,B) на (A,B),
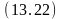 на
(A,B).
на
(A,B).
Таким образом, снова имеем истинные атомы на (A,B), на (B, Стол), на (D, Стол). Согласно правилу введения конъюнкции, вновь делаем заключение об истинности целевой формулы
на (A,B) на (B, Стол) на (С, Стол) на (D, Стол) .
На этом прямой вывод с использованием обобщенного правила резолюции завершён.
Достоинством использования обобщенного правила резолюции для прямого вывода является способность выводить большое количество формул по сравнению с выводом на основе обобщенного правила модус поненс. В процессе вывода база знаний по-прежнему разрастается за счёт занесения в неё вновь выводимых формул. Некоторые из этих формул могут оказаться ненужными для вывода целевой формулы.
Как
уже отмечалось, Робинсон предложил
использовать обобщенную резолюцию для
создания стратегии вывода, в основе
которой лежит опровержение,
или доведение
до противоречия.
Идея этой стратегии вывода состоит в
следующем. Предположим необходимо
вывести истинность целевой формулы
.
делается опровержение этой формулы,
т.е. предполагается истинным её отрицание
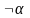 .
Эта формула, которая является отрицанием
целевой, заносится в базу знаний. После
этого, если, начиная обратный вывод с
формулы
,
удастся установить противоречие, т.е.
вывести пару литералов
и
.
Эта формула, которая является отрицанием
целевой, заносится в базу знаний. После
этого, если, начиная обратный вывод с
формулы
,
удастся установить противоречие, т.е.
вывести пару литералов
и
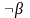 ,
то считается, что сделанное предположение
об истинности отрицания целевой формулы
ошибочно (опровергнуто) и делается
заключение об истинности целевой формулы
.
Если в результате рассмотрения всех
возможных путей вывода такого противоречия
установить не удаётся, то считается,
что целевая формула является ложной.
,
то считается, что сделанное предположение
об истинности отрицания целевой формулы
ошибочно (опровергнуто) и делается
заключение об истинности целевой формулы
.
Если в результате рассмотрения всех
возможных путей вывода такого противоречия
установить не удаётся, то считается,
что целевая формула является ложной.
Рассмотрим стратегию обратного вывода на основе опровержения для примера с кубиками.
Обратный вывод на основе опровержения и обобщенной резолюции. Как уже отмечалось, вывод истинности целевой формулы может лсуществляться по очереди литерал за литералом. Поэтому рассмотрим его только для одно литерала на (A,B) целевой формулы (13.7). Опровержение литерала на (A,B) является литерал на (A,B). Обратный вывод начинается именно с этого литерала. для того чтобы можно было детально проследить процесс вывода, будем записывать на каждом шаге вывода с помощью обобщенной резолюции три формулы – две исходные и резольвенту, нумеруя по ходу вывода получаемые резольвенты, а также указывая для каждого шага используемые подстановки и подчёркивая те литералы, которые в резольвенту не попадают:
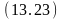 на
(A,B);
на
(A,B);
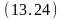 на
(A,
Стол)
свободен (A)
свободен (B)
на
(A,
Стол)
свободен (A)
свободен (B)
переместить (A,B) на (A,B);
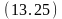 на
(A,
Стол)
свободен (A)
свободен (B)
на
(A,
Стол)
свободен (A)
свободен (B)
переместить (A,B) ;
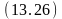 Ø
на
(A,
Стол)
Ú
Ø
свободен (A)
Ú
Ø
свободен (B)
Ú
Ø
на
(A,
Стол)
Ú
Ø
свободен (A)
Ú
Ø
свободен (B)
Ú
Ú Ø переместить (A,B) ;
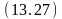 Ø
на
(A,
Стол)
Ú
Ø
свободен (A)
Ú
Ø
свободен (B)
Ú
Ø
на
(A,
Стол)
Ú
Ø
свободен (A)
Ú
Ø
свободен (B)
Ú
Ú переместить (A,B) ;
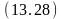 Ø
на
(A,
Стол)
Ú
Ø
свободен (A)
Ú
Ø
свободен (B);
Ø
на
(A,
Стол)
Ú
Ø
свободен (A)
Ú
Ø
свободен (B);
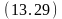 Ø
на
(A,
Стол)
Ú
Ø
свободен
(A)
Ú
Ø
свободен (B);
Ø
на
(A,
Стол)
Ú
Ø
свободен
(A)
Ú
Ø
свободен (B);
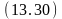 свободен
(A);
свободен
(A);
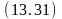 на
(A,
Стол)
Ú
Ø
свободен
(B)
;
на
(A,
Стол)
Ú
Ø
свободен
(B)
;
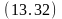 на
(A,
Стол)
Ú
Ø
свободен (B)
;
на
(A,
Стол)
Ú
Ø
свободен (B)
;
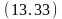 Ø
на
(A,
y)
Ú
Ø
свободен (A)
переместить
(A,
Стол)
Ø
на
(A,
y)
Ú
Ø
свободен (A)
переместить
(A,
Стол)
на (A, Стол);
 Ø
на
(A,
y)
Ú
Ø
свободен (A)
переместить
(A,
Стол)
Ø
на
(A,
y)
Ú
Ø
свободен (A)
переместить
(A,
Стол)
Ø свободен (B);
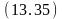 Ø
на
(A,
y)
Ú
Ø
свободен
(A)
переместить
(A,
Стол)
Ø
на
(A,
y)
Ú
Ø
свободен
(A)
переместить
(A,
Стол)
Ø свободен (B);
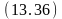 свободен
(A);
свободен
(A);
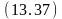 Ø
на
(A,
y)
Ú
переместить
(A,
Стол)
Ø
свободен (B);
Ø
на
(A,
y)
Ú
переместить
(A,
Стол)
Ø
свободен (B);
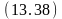 Ø
на
(D,B)
Ú
свободен (D)
переместить
(D,
Стол)
Ø
на
(D,B)
Ú
свободен (D)
переместить
(D,
Стол)
Ø свободен (B);
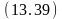 Ø
на
(D,B)
Ú
свободен (D)
переместить
(D,
Стол) ;
Ø
на
(D,B)
Ú
свободен (D)
переместить
(D,
Стол) ;
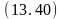 Ø
на
(D,B)
Ú
свободен (D)
Ú
свободен (B)
;
Ø
на
(D,B)
Ú
свободен (D)
Ú
свободен (B)
;
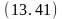 Ø
на
(D,B)
Ú
свободен (D)
Ú
свободен (B)
;
Ø
на
(D,B)
Ú
свободен (D)
Ú
свободен (B)
;
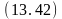 свободен
(D)
;
свободен
(D)
;
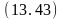 Ø
на
(D,B)
Ú
свободен (B)
;
Ø
на
(D,B)
Ú
свободен (B)
;
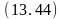 Ø
на
(D,B)
Ú
свободен (B)
;
Ø
на
(D,B)
Ú
свободен (B)
;
 Ø
на
(D,B);
Ø
на
(D,B);
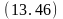 свободен
(B)
;
свободен
(B)
;
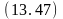 свободен
(B)
;
свободен
(B)
;
 Ø
свободен (B)
;
Ø
свободен (B)
;
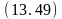 Nil.
Nil.
Преобразование произвольной формулы логики предикатов первого порядка в клаузальную форму. Применение обощенного правила резолюции требует представления формул в каузальной форме. Здесь мы покажем, с помощью каких эквивалентных преобразования любая произвольная формула логики предикатов первого порядка может быть преобразована в каузальную форму. Процедуру преобразования представим в виде отдельных шагов.
Исключение
импликаций.
Из логики высказываний известно, что
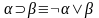 .
Поэтому на первом шаге с помощью этой
формулы исключаем все импликации.
.
Поэтому на первом шаге с помощью этой
формулы исключаем все импликации.
Перемещение знака отрицания () непосредственно к атомам. В клаузах отрицание допустимо только перед атомами. Поэтому используя перечисленные ниже законы Де Моргана, эквивалентности кванторов и двойного отрицания, перемещаем знак отрицания непосредственно к атомам:
 ,
,
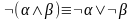 ,
,
 ,
,
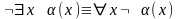 ,
,
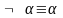 .
.
Переименование
переменных.
Во всех формулах, в которых встречаются
кванторы, использующие одни и те же
связанные переменные, как, например, в
формуле
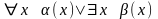 ,
переименовываем связанные переменные
таким образом, чтобы они были индивидуальными
для каждого квантора. Например, для
нашего примера это может быть использование
переменной
вместо переменной
для квантора существования. В результате
получится формула
,
переименовываем связанные переменные
таким образом, чтобы они были индивидуальными
для каждого квантора. Например, для
нашего примера это может быть использование
переменной
вместо переменной
для квантора существования. В результате
получится формула
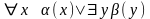 .
.
Перемещение
кванторов влево.
После предыдущего шага, в результате
которого каждый квантор использует
свои связанные переменные, обозначения
которых не совпадают с переменными
других кванторов все кванторы перемещаем
влево. Так, например, простая
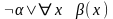 после перемещения квантора влево примет
вид
после перемещения квантора влево примет
вид
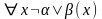 .
.
Сколемизация.
Сколемизацией
называется специфический приём удаления
кванторов существования. В простейшем
случае – это замена формулы
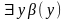 на формулу
на формулу
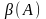 ,
где
является константой, которая ранее не
встречалась. В общем случае, когда
переменная, которая связывается квантором
существования. встречается в каком-либо
литерале вместе с переменными, связанными
квантором общности, приходится, чтобы
избавиться от квантора общности, вводить
специальную функцию, которая зависит
от переменных, связанных квантором
обшности, вместо переменной, связанной
квантром существования.
,
где
является константой, которая ранее не
встречалась. В общем случае, когда
переменная, которая связывается квантором
существования. встречается в каком-либо
литерале вместе с переменными, связанными
квантором общности, приходится, чтобы
избавиться от квантора общности, вводить
специальную функцию, которая зависит
от переменных, связанных квантором
обшности, вместо переменной, связанной
квантром существования.
Так, если имеем формулу
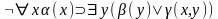 ,
,
то
здесь литерал
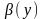 может означать, например, наличие
некоторого свойства, именуемого
предикатным символом
,
у объекта, именуемого переменной
,
а атом
может означать, например, наличие
некоторого свойства, именуемого
предикатным символом
,
у объекта, именуемого переменной
,
а атом
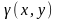 задаёт отношение между объектами
.
Объект, который обозначен переменной
,
определяется в этом случае значением
переменной
и может быть заменен на ранее не
встречавшуюся функцию
задаёт отношение между объектами
.
Объект, который обозначен переменной
,
определяется в этом случае значением
переменной
и может быть заменен на ранее не
встречавшуюся функцию
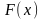 ,
которая обычно называют функцией
Сколема.
После такой замены квантор сущестования
может быть удален, а формула приобретает
вид
,
которая обычно называют функцией
Сколема.
После такой замены квантор сущестования
может быть удален, а формула приобретает
вид
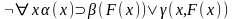 .
.
Распределение конъюнкций относительной дизъюнкций. Это распределение осуществляется на основе использования дистрибутивного закона
 .
.
Перемещение
скобок к концу и началу.
На этом шаге формулы со скобками типа
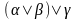 или
или
 приводятся соответственно к виду
приводятся соответственно к виду
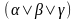 или
или
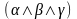 .
После этого шага исходная формула
преобразуется в нормальную конъюнктивную
форму, которая является конъюнкцией
дизъюнкцией литаралов. Каждая дизъюнкция
литералов является клаузой.
.
После этого шага исходная формула
преобразуется в нормальную конъюнктивную
форму, которая является конъюнкцией
дизъюнкцией литаралов. Каждая дизъюнкция
литералов является клаузой.
