Тема 12.2 Тройной интеграл
ПК-2 [12.2.1]
ВЫБОР
Тройной интеграл
от функции
по области V
:
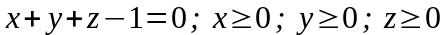имеет вид…
В
+
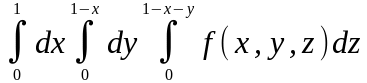
В -
В -
В -
ПК-2 [12.2.2]
ВЫБОР
Тройной интеграл
от функции
по области V
:
имеет вид…
В
+
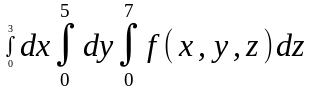
В -
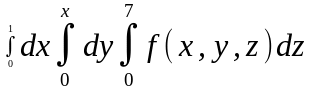
В -
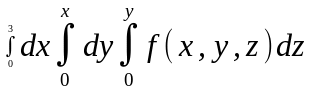
В -
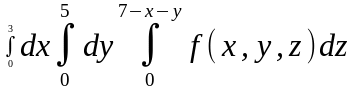
ПК-3 [12.2.3]
ВЫБОР
Тройной интеграл
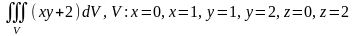равен…
В- 2
В- 3,5
В- 6,5
В+ 5,5
Тема 12.3 Криволинейные интегралы
ОК-1 [12.3.1]
ВЫБОР
Криволинейным интегралом 1-го типа от функции , по длине дуги гладкой кривой С, является интеграл…
В
+
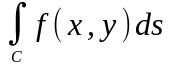
В -
В -
В -
ОК-1 [12.3.2]
ВЫБОР
Криволинейным интегралом 2-го типа от функции , по гладкой кривой С, является интеграл…
В
+
В -
В -
В -
ОК-1 [12.3.3]
ВЫБОР
Криволинейный
интеграл 1-го типа от функции
,
по длине дуги гладкой кривой С,
заданной уравнением
,
,
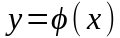вычисляется по формуле…
В
+
В -
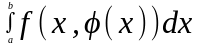
В -
В -
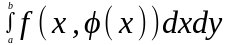
ОК-1 [12.3.4]
ВЫБОР
Криволинейный
интеграл 1-го типа от функции
,
по длине дуги гладкой кривой С,
заданной параметрическими уравнениями:
,
,
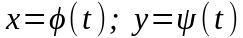вычисляется по формуле…
В
+
В -
В -
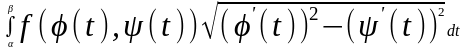
В -
ПК-2 [12.3.5]
ВЫБОР
Формула Грина для плоской области D, ограниченной кривой С ,
имеет вид…
В
+
В -
В -
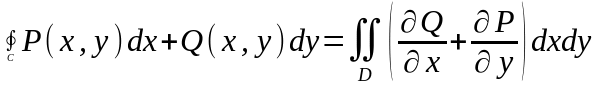
В -
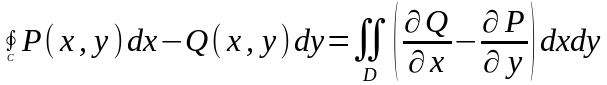
ОК-1 [12.3.6]
ВЫБОР
Криволинейный интеграл 1-го рода используется для вычисления …
В- масса неоднородного стержня
В- площади плоской фигуры
В- объема тела вращения
В+ длины плоской или пространственной кривой
ПК-3 [12.3.7]
ВЫБОР
Для того, чтобы
криволинейный интеграл
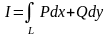не зависел от пути интегрирования в
односвязной области D,
в которой функции Р(х,у) и Q(x,y)
непрерывны вместе со своими частными
производными, необходимо и достаточно,
чтобы в каждой точке этой области
выполнилось условие …
В-
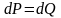
В-
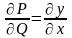
В-
В+
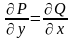
ОК-1 [12.3.8]
ВЫБОР
Криволинейный интеграл 2-го рода используется для вычисления …
В- масса неоднородного стержня
В+ площади плоской фигуры
В- объема тела вращения
В- длины плоской или пространственной кривой
Тема 12.4 Поверхностные интегралы и векторные поля
ОК-1 [12.4.1]
ВЫБОР
Поверхностный интеграл 1-го рода используется для вычисления …
В- масса неоднородного стержня
В+ площади поверхности
В- объема тела вращения
В- длины плоской или пространственной кривой
ПК-2 [12.4.2]
ВЫБОР
Дивергенцией
векторной функции
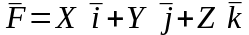называется выражение…
В
+
В -
В -
В -
ОК-1 [12.4.3]
ВЫБОР
Интеграл по
поверхности S
, выраженный через двойной интеграл по
проекции S
на плоскость Оху равен…
В-
В-
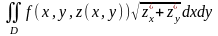
В-
В+
ПК-2 [12.4.4]
ВЫБОР
Оператором
Лапласа от функции
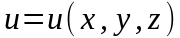является выражение…
В
+
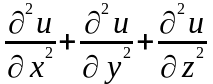
В -
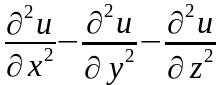
В -
В -
ПК-3 [12.4.5]
ВЫБОР
Векторное поле называется соленоидальным, если для него выполняется равенство…
В
+
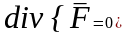
В -
В -
В -
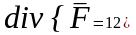
ПК-3 [12.4.6]
ВЫБОР
Векторное
поле
называется потенциальным, если для
некоторой скалярной функции
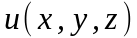выполняется равенство…
В
+
В -
В -
В -
ПК-3 [12.4.7]
ВЫБОР
Векторное поле называется безвихревым если выполняется равенство…
В
+
В -
В -
В -
