3.2 Шумы квантования

В ЦСП, в результате квантования сигнала по уровню, возникают ошибки, поскольку реальные мгновенные значения сигнала приравниваются ближайшим разрешенным значениям уровней квантования. Эти ошибки воспринимаются как флуктуационные шумы с равномерной спектральной плотностью и называются шумами квантования. Шумы квантования представляют собой стационарный случайный эргодический процесс.

При равномерном квантовании (с постоянным шагом квантования), мощность шума квантования в полосе частот канала равна:

Р_шк = (U²_p/12)·(2·F_к/f_д), Вт (9)

Р_шк =0,000024*0,775=0,0000186 Вт

где U_p- величина шага квантования, В;

F_к- ширина полосы частот канала ТЧ, F_к=3,1 кГц;

f_д- частота дискретизации сигнала, f_д=8 кГц.

Величина шага квантования:

U_p = 2·U_огр/N_кв, В (10)

U_p =2*1,112/128=0,017

где U_огр- напряжение ограничения сигнала в кодере (максимальное значение сигнала на входе кодера), В;

N_кв- число шагов квантования в кодере, причем N_кв=2^mp,

где m_p- число разрядов двоичного кода при равномерном квантовании.

В аппаратуре ЦСП используется нелинейное кодирование с характеристикой кoмпрессии A-87,6/13. Характеристика состоит для положительных значений сигнала из 8 сегментов (0÷7), в каждом из которых 16 шагов квантования. Всего N_кв=8∙16=128 шагов квантования (1-16, 17-32, ... 113-128). Шаг квантования U_н постоянен внутри каждого сегмента и увеличивается в 2 раза при переходе к следующему сегменту. В 0-м и 1-м сегментах самый минимальный шаг квантования- U_н0, а в 7-м сегменте- самый максимальный шаг квантования- 64∙U_н0. То же самое и для отрицательных значений сигнала.

Для i-го сегмента можно записать:

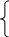U_н0, В при i = 0, 1

U_нi = (11)

2^{(i -1)}·U_н0, В при i = 2, ...7

Напряжение ограничения сигнала в кодере соответствует значению: U_огр=(16∙U_н0)+(16∙U_н0)+(16∙2∙U_н0)+(16∙4∙U_н0)+…+(16∙64∙U_н0)=2048∙U_н0.

Тогда минимальное значение шага квантования:

U_н0=U_огр/2048=U_огр/2¹¹=2^-11·U_огр, В (12)

Напряжение ограничения определяется по соотношению:

U_огр=U_макс=0,775·10^{(0,05·рмакс)}, В (13)

Согласно рекомендации МСЭ (МККТТ), порог ограничения (максимальное значение уровня сигнала) для характеристики кодера A-87,6/13 следует принять равным р_макс=+3,14 дБм0. В этом случае, U_огp=0,775·10^(0,05·3,14)=1,112 В, U_н0=1,112/2048=0,54·10^-3 В=0,54 мВ.

Обозначив U_вх/U_огр=x и учитывая, что 0х1, найдем х_н.i и х_в.i, соответствующие нижней и верхней границам каждого сегмента.

Таблица 3.1 - Границы сегментов при нелинейном кодировании

№ сегмента	0	1	2	3	4	5	6	7
хн.i	2- = 0	2-7	2-6	2-5	2-4	2-3	2-2	2-1
хв.i	2-7	2-6	2-5	2-4	2-3	2-2	2-1	20 = 1

Определим защищенность от шумов квантования для i- го сегмента:

- для сегментов i =0 и i =1:

А_з.кв.i=10·lg[Р_с/(Р_шк·К_п²)]=10·lg{(U_огр·х_i)²/[(U_н0²/12)·(2·F_к·К_п²/f_д)]} (14)

где Р_с- мощность сигнала;

К_п- псофометрический коэффициент напряжения, К_п=0,75.

Подставляя U_н0=2^-11·U_огр и значения F_к, К_п, f_д получим:

А_з.квi =20·lgх_i + 80,6 дБ (15)

Для нижней границы

А_з.кв0 =20·lg0

А_з.кв1 =20·lg2^-7 +80,6=-16,44

Для верхней границы

А_з.кв0 =20·lg2^-7 +80,6=-16,44

А_з.кв0 =20·lg2^-6 +80,6=-2,57

Для сегментов i=2, 3...7, с учетом вышеприведенных подстановок, имеем:

(U_огр·х_i)² х_i²

А _з.кв.i =10·lg = 10·lg =

(U_н0·2^i-1)²/12·(2·F_к)/f_д·K_п² (2^-11·2^i-1)²/12·(2·F_к)/f_д·K_п ²

= 20·lg(х_i·2^12-i) + 14,4 дБ (16)

Для нижней границы

А_з.кв.2 = 20·lg(2^-6·2^12-2) + 14,4=125,3 дБ

А_з.кв.3 = 20·lg(2^-5·2^12-3) + 14,4=125,3 дБ

А_з.кв.4 = 20·lg(2^-4·2^12-4) + 14,4=125,3 дБ

А_з.кв.5 = 20·lg(2^-3·2^12-5) + 14,4=125,3 дБ

А_з.кв.6 = 20·lg(2^-2·2^12-6) + 14,4=125,3 дБ

А_з.кв.7 = 20·lg(2^-1·2^12-7) + 14,4=125,3 дБ

Для верхней границы

А_з.кв.2 = 20·lg(2^-5·2^12-2) + 14,4=46,58 дБ

А_з.кв.3 = 20·lg(2^-4·2^12-3) + 14,4=46,58 дБ

А_з.кв.4 = 20·lg(2^-3·2^12-4) + 14,4=46,58 дБ

А_з.кв.5 = 20·lg(2^-2·2^12-5) + 14,4=46,58 дБ

А_з.кв.6 = 20·lg(2^-1·2^12-6) + 14,4=46,58 дБ

А_з.кв.7 = 20·lg(2⁰ ·2^12-7) + 14,4=46,58 дБ

Подставляя значения х_нi и х_вi , мы оценили минимальное А_з.кв.i и максимальное А_з.кв.i значения защищенности для нижней и верхней границы соответствующего сегмента характеристики. Так как вне зависимости от i, величины х_i·2^(12-i)=const, то и защищенности от шумов квантования А_з.кв.i будут одинаковы во всех сегментах, линейно возрастая от А_з.кв.i до А_з.кв.i .