6.5. Розрахунок поля температур в однорідній штабі за неявною схемою

У вище розглянутому прикладі застосування явного методу розв’язання диференціального рівняння (6.1) апроксимовані температури у вузлах сітки залежали тільки від i . З розгляду рис. 6.5 випливає, що за цим підходом визначення температури v можливе тільки в зоні, позначеній літерою А. Саме вузли цієї зони задіяні при визначенні розподілу температури в штабі. У той же час відомо, що для визначення поля температур, обумовленого диференціальним рівнянням (6.1) та початковими і граничними умовами (6.2), необхідно проводити розрахунки як зоні А, так і в зоні В.

Явна різницева схема зручна в застосуванні але стійка лише при виконанні умови

Цю обставину треба враховувати при виборі кроку за часом і довжиною штаби.

Р озв’яжемо рівняння (6.1) з початковими і граничними умовами (6.2) за дещо іншою схемою апроксимаційного подання похідних, яку називають неявною схемою. Запишемо скінченні різниці похідних у наступному вигляді:

(6.8)

Н а відміну від попереднього прикладу, коли друга похідна визначалася в j-му шарі з часом , зараз вона знаходиться із значеннями апроксимованої температури в шарі j+1, якому відповідає час . Це призводить до іншої схеми розташування чотирьох вузлових точок (рис. 6.6), задіяних в обчислювальному процесі.

Розв’яжемо рівняння (6.8) відносно , яке запишемо в правій частині розв’язку. Будемо мати вираз:

. (6.9)

Коефіцієнт λ має той же сенс, що й у формулі 6.4.

Отже, на відміну від вище розглянутої явної схеми кожне різницеве рівняння другої схеми містить на кожному новому шарі три невідомі значення, які неможливо визначити відразу ж, як це має місце в явній схемі. При цьому друга різницева схема складається з лінійних триточкових рівнянь, тобто кожне рівняння містить невідому функцію в трьох точках нового шару.

Граничні та початкові умови залишаються тими ж самими, що й у вище розглянутому прикладі:

,

,

.

Рівняння (6.9) можуть бути записані для кожної вузлової точки з діапазону для будь-якого моменту часу, що призведе до системи з М – 1 рівнянь з М – 1 невідомими .

Розглянемо розв’язання наступної системи лінійних рівнянь:

(6.10)

Цю систему рівнянь зручніше записати в такому вигляді:

(6.11)

У системах (6.10) і (6.11) для скорочення запису індекси (j + 1) при всіх температурах v пропущені. Праві частини рівнянь (6.10), які є відомими величинами, для спрощення запису позначені як , де

Система рівнянь (6.11) має назву тридіагональної матриці, оскільки заповненими є тільки три діагональні елементи кожного рядка. Цю систему можна розв’язати відомим методом Гауса, але при цьому мають бути заповнені всі нульові члени, тому матриця буде мати значний розмір і буде виконано багато зайвих обчислювальних операцій, що є недоцільним.

Краще для розв’язання тридіагональної матриці застосовувати так званий метод прогонки в наступній формі:

. (6.12)

Коефіцієнти _i і γ_i будуть розглянуті трошки нижче.

Підстановка виразу (6.12) до системи (6.11) призведе до наступного запису:

,

з якого можна визначити v_i:

.

Це дає можливість застосувати наступну рекурсивну схему:

;

.

З першого рівняння системи (6.11) маємо

,

де .

Коефіцієнт γ₁ дорівнює

Із останнього рівняння системи (6.11) можна отримати

.

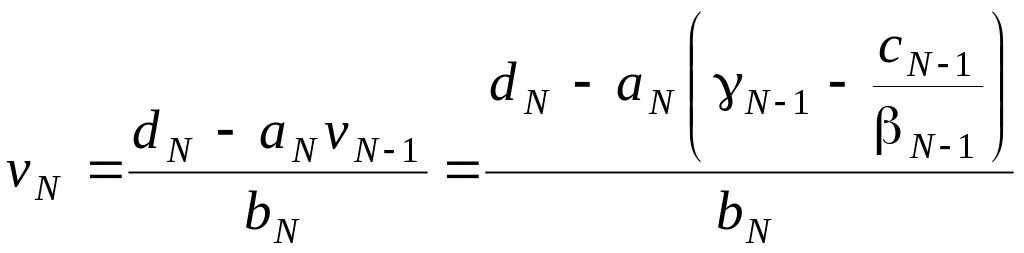Звідки

.

Таким чином, алгоритм розв’язання тридіагональної матриці у стислому вигляді запишеться наступним чином:

в якому

Таким чином, у разі неявної схеми, щоб розрахувати значення функції температур в кожен наступний момент часу, тобто, щоб перейти на наступний шар за часом, необхідно кожного разу вирішувати методом прогонки лінійну систему.

Результати розрахунків за неявною схемою в графічному вигляді наведені на рис. 6.7. Їм відповідають криві без додаткових позначень. На цьому ж рисунку для порівняння показані результати розрахунків поля температур в однорідній штабі, отримані із застосуванням явної схеми. Це криві з нанесеними на них точками, вони повністю відповідають графічним даним, наведеним на рис. 6.4.

Як випливає з розгляду рис. 6.7, результати розрахунків проведені за явною і неявною схемами дуже близькі, що і очікувалося.

Зрозуміло, що коло задач, для розв’язання яких застосовується числове математичне моделювання, не обмежується розрахунками температурних полів. Існує безліч задач, рішення яких можна отримати ретельно підібраними числовими методами.

Н а завершення треба відзначити, що сучасні числові методи і потужні ЕОМ надали можливість розв’язувати такі задачі з числового математичного моделювання, про які раніше можна було тільки мріяти. Але застосовувати числові методи не так просто. Треба пам’ятати, що ЕОМ уміють виконувати тільки арифметичні дії та логічні операції. Тому окрім розробки математичної моделі необхідна ще розробка відповідного алгоритму, який зводить всі розрахунки до послідовності арифметичних і логічних дій. Вибирати числову математичну модель та алгоритм треба з урахуванням швидкодії комп’ютера та об’єму його пам’яті: занадто складна модель може виявитися комп’ютеру не під силу, а дуже проста – не відповідатиме фізичній точності об’єкта, що вивчається засобами числового математичного моделювання.

Безпосередньо алгоритм і програма для ЕОМ мають бути ретельно перевірені. Але перевірка програми справа нелегка, про що свідчить популярне твердження: "В будь-якій як завгодно малій програмі є щонайменше одна помилка". Про це треба обов’язково пам’ятати, розв’язуючи задачі числового математичного моделювання.

12

ЛЕКЦІЯ № 10 (алгоритми та методи обчислень)