Вариант 3

Задача 1

В урне содержится 6 черных и 5 белых шаров. Случайным образом вынимают 5 шаров. Найти вероятность того, что среди них имеется: а) ровно 3белых шара б) меньше, чем 3 белых шара, в) хотя бы 1 белый шар.

Задача 2

Вероятность возврата в срок потребительского кредита каждым из 220 заемщиков в среднем равна 0,95. Найти вероятность того, что к назначенному сроку кредит вернут:

А) не менее 180 человек и не более 200 человек; Б) не менее 200 человек; В) не более 199 человек.

Задача 3

Дискретная случайная величина задана таблицей.

ci		-5		-2				0			2		5
Pi		1			1			1			1		p5
		48		8				2			3

Найти р₅ , математическое ожидание, дисперсию, среднее квадратическое отклонение.

Задача 4

Случайная величина Х задана функцией распределения

F(x) =

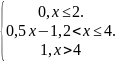
1. Найти f(х), М(Х), D(X).

2. Построить графики f(х), F(x).

3. Вычислить Р (1< x 3).

Задача 5

Задана выборка Х. Для выборки Х необходимо:

1.составить интервальный ряд распределения;

2.найти выборочную среднюю, моду, медиану. Выборочную дисперсию. Выборочное среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и эксцесс;

3.построить гистограмму частот;

4.найти эмпирическую функцию распределения и построить ее график;

68	50	70	77	54		73	74	65	55	73
63	34	58	68	73		75	65	64	72	72
59	62	72	58	69		56	69	67	68	61
72	67	69	61	63		68	52	66	58	72
61	70	63	63	63		55	71	68	68	66
77	72	72	73	73		62	58	57	64	67
70	82	60	52	69		72	63	67	63	59
74	79	59	74	57		69	62	73	71	64
68	78	59	69	61		63	74	62	77	82
73	74	65	55	73		70	61	64	69	73