Сигналов с прямоугольным () и гауссовым () спектром

Рис. 5.16. Зависимость числа обусловленности матрицы С от n при =1.0 для сигналов с прямоугольным () и гауссовым () спектром

Из графиков видно, что с увеличением размерности входного вектора число обусловленности резко возрастает. Этот рост тем больше, чем меньше относительная полоса спектра сигнала .

Таким образом, в случаях, когда размерность входного вектора превышает 10 отсчетов и <0.3 вычисление коэффициентов множественной регрессии через элементы обратной матрицы может повлечь за собой сильное накопление ошибок (более, чем на три порядка). Полученные таким образом результаты с трудом можно считать достоверными. В качестве альтернативного подхода предложено получить коэффициенты регрессии при помощи нейронной сети.

Получение коэффициентов множественной регрессии и обращение матриц при помощи нейронной сети

При большой размерности задачи обращение матрицы становится весьма трудоемкой задачей. Чтобы решить эту проблему, можно воспользоваться нейросетевым методом и получить коэффициенты множественной регрессии интервалов между нулями как веса w_ij при обучении нейросети (П. 5.1).

Рассмотрим однослойную нейронную сеть с n входами и одним выходом, обрабатывающую интервалы между нулями нормального стационарного случайного процесса, – длительности i–го интервала.

Так как множественные коэффициенты регрессии есть веса в линейном преобразовании вида:

то веса w_ik выполняют роль множественных коэффициентов регрессии (5.4)

П. 5.1, если принять out_i = x_i. (рис.5.17)

Рис.5.17. Однослойная нейронная сеть с четырьмя входами и одним выходом для получения коэффициентов множественной регрессии

Сеть обучалась на математической модели сигнала по алгоритму обратного распространения [24].

Сглаженная зависимость величины ошибки на выходе сети от номера итерации приведена на рис. 5.18.

Рис.5.18. Зависимость величины ошибки при обучении сети от номера итерации

Как показывают результаты расчетов (рис.5.18), величина ошибки достигает приемлемо малой величины (  10^-5) уже через 100000 итераций.

Полученные в качестве весов такой сети коэффициенты множественные коэффициенты регрессии первого интервала на остальные при общей размерности задачи равной семи для различных  приведены на рис. 5.19– 5.20.

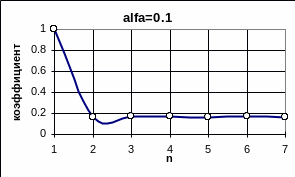
Рис.5.19. Коэффициенты множественной регрессии 1-го интервала на 6 остальных при  = 0.1

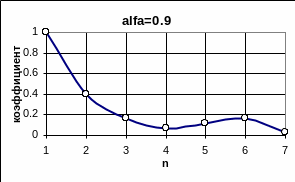
Рис.5.20. Коэффициенты множественной регрессии 1-го интервала на 6 остальных при  = 0.9

Применение предлагаемого нейросетевого подхода позволяет получить оценки остаточных средних значений квадратов регрессионных представлений и коэффициентов множественной начальной регрессии интервалов между нулями сигналов и помех как весовые коэффициенты , получаемые при обучении нейросети с использованием метода обратного распространения. Результаты исследований показали, что по предлагаемой методике легко могут быть вычислены требуемые статистические характеристики даже при нормированных коэффициентах корреляции параметров сигналов стремящихся к единице.

В П.6.3 показано, что при , , где n- размерность входного вектора. Это позволило осуществить проверку правильности выполненных расчетов. График рис.5.19 подтверждает тот факт, что при   0 все КМНР стремятся к одинаковому значению: _1i = 1/(n-1), где n - размерность входного вектора. В нашем случае при n=7 = 1/6=0.16. С увеличением относительной ширины полосы усиливается вклад первых двух отсчетов.

Возможно распространить рассмотренный выше метод получения МКНР на задачу обращения ковариационнй матрицы (матрицы центральных моментов) и вычисления коэффициентов центральной регрессии. В этом случае для получения обратной матрицы необходимо, чтобы число выходов нейронной сети равнялось числу входов (рис.5.21).

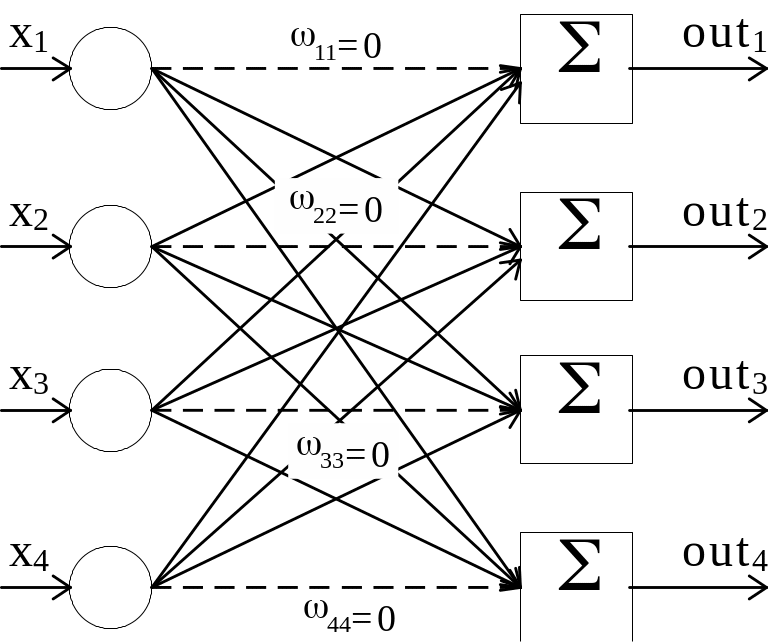
Рис.5.21. Структура нейронной сети для решения задачи обращения матрицы 44 при помощи множественных коэффициентов регрессии

Блок-схема алгоритма получения обратной матрицы приведена на рис.5.22. Исходная матрица задается как матрица ковариационных моментов. Затем на вход нейронной сети подаются центрированные информативные признаки реализаций реального сигнала, или исходя из матрицы ковариационных моментов, одним из известных методов моделируется случайный вектор признаков, который является входным вектором нейронной сети. Таким образом создается входное множество для последующего обучения нейронной сети.

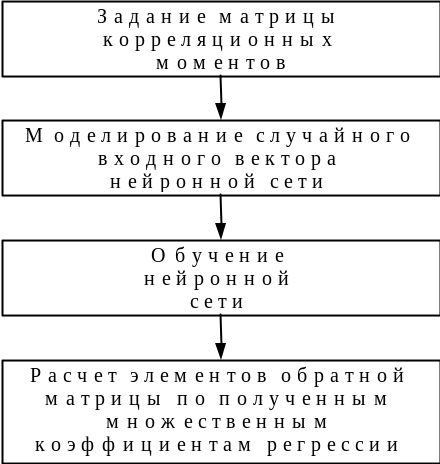
Рис. 5.22. Блок-схема алгоритма получения обратной матрицы через коэффициенты множественной регрессии при помощи нейронной сети

Важно отметить, что нейронная сеть является однослойной с линейной функцией активации, что значительно сокращает затраты времени на ее обучение и требования к ресурсам вычислительной машины. После обучения нейронной сети ее веса, представляющие собой коэффициенты множественной регрессии (в рассматриваемом случае центральные)

,

где – матрица, обратная матрице ковариационных моментов, используются для получения матрицы, обратной исходной матрице ковариационных моментов. Для этого необходимо вычислить на каждом выходе нейронной сети и остаточную дисперсию (П5.1). Таким образом получаются элементы матрицы, обратной матрице ковариационных моментов.

Среди недостатков предложенного метода можно отметить то, что при теоретических исследованиях исходная матрица задается как матрица ковариационных моментов и является симметричной. Кроме того, требуется предварительная генерация множества случайных векторов, которые затем подаются на вход сети.

На практике рассмотренный метод обращения матриц корреляционных (ковариационных) моментов требуется применять только тогда, когда необходимо в явном виде оценить элементы обратной матрицы. В рассматриваемых случаях этого не требуется, т.к. при получении МКНР как весов нейронной сети происходит неявное обращение матрицы.