5.2. Сравнение классических и регрессионных методов сокращения размерности и выбора информативных признаков сигналов
Сравнение методов выбора информативных признаков сигналов проведено на примере задачи распознавания акустических сигналов самолета и вертолета на основе реализаций, полученных в результате экспериментальных исследований и математического моделирования.
Для сравнения с методом выбора информативных признаков и сокращения их размерности на основе коэффициентов множественной начальной регрессии (КМНР) (без использования оценок математических ожиданий) рассмотрим метод дискриминантного анализа и метод главных компонент.
При дискриминантном анализе для
формирования критериев разделимости
классов использованы матрицы рассеяния
внутри классов
и между классами
[9, 25].
Матрица рассеяния внутри классов показывает разброс объектов относительно векторов математических ожиданий классов:
, (5.16)
,
где
– вектор средних значений l-мерной
выборки, принадлежащей j-му классу.
Матрица пропорциональна ковариационной выборочной матрице для совокупности l – мерных данных. Она симметричная, положительно определенная и, как правило, невырожденная.
Матрица рассеяния между классами может быть определена несколькими способами. Наиболее распространенный из них описывается выражением:
.
Эта матрица также симметричная положительно определенная, но ее ранг будет самое большее равен единице, т.к. она является внешним произведением двух векторов.
Наиболее распространены 4 критерия, использующих эти матрицы:
,
,
,
(где - множитель Лагранжа, с – константа)
,
где
– след матрицы
.
Критерий J4 является наиболее распространенным. Критерии J1 и J2 инвариантны относительно любого невырожденного линейного преобразования, тогда как критерии J3 и J4 зависят от системы координат.
Одно из важных преимуществ этих критериев заключается в том, что эти критерии можно использовать и при наличии многих классов (множественный дискриминантный анализ). Требуется только обобщить определение матриц рассеяния. Однако при увеличении числа классов эти критерии, как и любые другие, становятся все менее точными индикаторами разделимости классов. Поэтому оптимально использовать только парную классификацию.
В рассматриваемой задаче для анализа разделимости классов {самолет} и {вертолет} использованы критерии J1 и J4.
В качестве критерия разделимости двух классов также использовалось расстояние Бхатачария. Для нормальных распределений расстояние Бхатачария имеет вид:
,
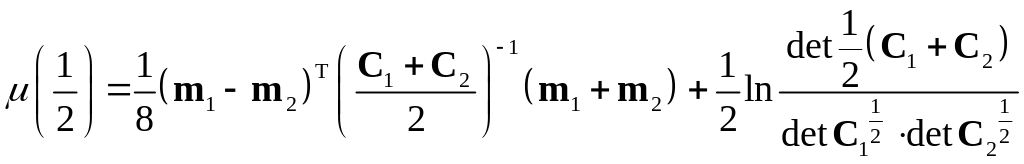где
,
–
вектора средних значений выборок каждого
класса;
и
– ковариационные матрицы.
Расстояние Бхатачария является эффективным критерием разделимости двух классов. Этот критерий позволяет определить верхнюю границу вероятности ошибки для случая равных априорных вероятностей классов как
.
В классической теории распознавания образов для сокращения размерности векторов признаков широко используется разложение Карунена-Лоэва [9, 12, 25]. Его дикретный аналог - метод главных компонент (ГК).
Метод ГК оперирует центральными (ковариационными) моментами случайных отсчетов сигналов и предполагает нахождение собственных векторов и собственных значений по заданной ковариационной матрице.
Для сокращения размерности векторов признаков при решении задачи обнаружения и распознавания самолета и вертолета использован метод ГК. Для нахождения главных компонент из всех характеристик исследуемой генеральной совокупности существенное значение имеет только ковариационная матрица:
,
где
.
В общем случае i-й главной компонентой называется нормированная линейная комбинация р исходных признаков x(1), x(2), ..., x(p):
,
которая среди всех прочих линейных нормированных комбинаций, некоррелированных со всеми предшествующими, обладает наибольшей дисперсией. Таким образом, все главные компоненты пронумерованы в порядке убывания их дисперсий:
Dy(1) Dy(2)...Dy(p)
В выражении для i-ой главной
компоненты
есть i-й собственный вектор ковариационной
матрицы
.
Его компоненты определяются как
нормированное (
)
решение системы уравнений:
,
где i - i-й по величине корень следующего уравнения или i-е собственное число матрицы :
.
При этом дисперсия главной компоненты Dy(i)=i.
Разложение случайного вектора по
собственным векторам ковариационной
матрицы и есть дискретный аналог
разложения Карунена-Лоэва. Ковариационная
матрица
главных компонент y(1),
y(2),...,y(p) будет
иметь вид:
.
Обобщенная дисперсия сумма дисперсий (Dy(1)+Dy(2)+...+Dy(p)) главных компонент равны сумме дисперсий (Dх(1)+Dх(2)+...+Dх(p)) исходных признаков. Это дает некоторую основу при вынесении решения о том, сколько последних главных компонент можно без особого ущерба изъять из рассмотрения, сократив тем самым размерность исследуемого пространства.
Анализируя изменение относительной доли дисперсии:
,
вносимой первыми главными компонентами, в зависимости от числа главных компонент, можно определить число компонент, которое целесообразно оставить в рассмотрении. Так формируется вектор главных компонент (размерностью p), которые далее могут использоваться как информативные признаки.
Экспериментальные реализации акустических сигналов самолета и вертолета для подавления шума ветра были полученны на выходе фильтра высоких частот с частотой среза 200 Гц. Выбор длины реализации осуществлялся из соображений сохранения свойств стационарности и эргодичности случайного процесса на длине вводимой реализации. В результате для получения оценок энергетического спектра случайных процессов были выбраны длины реализаций, равные N=16384 отсчетам при частоте дискретизации F = 10000 Гц.
Рис. 5.3. Реализация сигнала самолета
Рис. 5.4. Реализация сигнала вертолета
На рисунках 5.3 и 5.4 приведены оцифрованные реализации сигналов самолета и вертолета ( по 512 отсчетов).
По имеющимся в распоряжении исходным последовательностям отсчетов 50 реализаций сигналов, были получены спектры самолета и вертолета.
Рис. 5.5. Сглаженная по 20 – ти отсчетам оценка спектральной плотности