
- •Глава 5. Нейросетевые алгоритмы систем обнаружения и распознавания сигналов
- •5.1. Сокращение размерности и выбор информативных признаков в автономных информационных системах с нейросетевыми трактами обработки сигналов
- •Алгоритм (5.11)
- •5.2. Сравнение классических и регрессионных методов сокращения размерности и выбора информативных признаков сигналов
- •Мощности реализации сигнала самолета
- •Мощности реализации сигнала вертолета
- •5.3. Применение нейросетевых и методов к решению задач вычисления множественных коэффициентов регрессии и обращения плохо обусловленных матриц Обусловленность вычислительной задачи
- •Обусловленность матриц корреляционных моментов информативных признаков
- •Сигналов с прямоугольным () и гауссовым () спектром
- •Получение коэффициентов множественной регрессии и обращение матриц при помощи нейронной сети
- •5.4. Робастное обучение нейросети
- •5.5. Вопросы практической реализации нейросетевых трактов в аис Формирование вектора признаков в нейросетевой системе распознавания акустических сигналов
- •Акустических сигналов самолета и вертолета Скорость обучения нейросети при различных функциях активации и количестве нейронов скрытого слоя
- •Скорость обучения и ошибки тестирования робастной нейросети
- •Активационной функцией
- •Активационной функцией
- •Нейросетевой тракт обработки интервалов между нулями входных реализаций
Глава 5. Нейросетевые алгоритмы систем обнаружения и распознавания сигналов
5.1. Сокращение размерности и выбор информативных признаков в автономных информационных системах с нейросетевыми трактами обработки сигналов
Одной из актуальных является задача существенного повышения помехозащищенности автономных информационных и управляющих систем (АИУС) ближней локации (БЛ) в условиях интенсивных искусственных активных и пассивных помех. Одним из путей решения этой проблемы является улучшение характеристик обнаружения и распознавания АИУС. Необходимость решения новых задач и усложняющиеся условия применения требуют разработки адаптивных АИУС и систем, обладающих свойствами робастности и непараметричности. Для улучшения рабочих характеристик необходимо повышать информативность рабочих каналов АИУС, которые могут быть основаны на различных физических принципах. В ближней локации случайные сигналы на входе и помехи имеют большой динамический диапазон амплитудных, частотных и временных характеристик и ярко выраженный нестационарный характер. Информативные параметры сигналов часто являются нецентрированными случайными величинами или процессами на ограниченном интервале наблюдения, для которых априорно не известны математические ожидания, оценить которые по нестационарной реализации также не представляется возможным.
В этих условиях невозможно применить традиционные методы статистических решений, требующие вычисления и обработки центрированных параметров сигналов, которые при неизвестных математических ожиданиях получить принципиально невозможно.
Снять ограничения, связанные с нестационарностью информативных параметров, позволяет переход в признаковое пространство, в котором каждая выборочная реализация отображается вектором, а ансамбль реализаций – областью. Для обработки информации в многомерном признаковом пространстве, при отмеченных выше особенностях АИС в ближней локации, необходимы эффективные методы выделения информативных признаков, обоснования решающих функций (разделяющих границ) в условиях априорной неопределенности в сложной помеховой обстановке. Важное значение в этих условиях играет сокращение времени на разработку систем и автоматизация процесса исследования.
Всем отмеченным выше требованиям удовлетворяет подход к созданию принципиально новых АИС, основанный на обработке в трактах АИС нецентрированных параметров сигналов и помех, на использовании в качестве априорной информации начальных моментов случайных процессов и на применении нейросетевых технологий для исследования и проектирования АИС нового поколения.
Предлагаемый подход предусматривает наличие на входе тракта обработки сигналов рассматриваемых АИС анализатора признаков, в котором осуществляется выделение первичных и вторичных информативных признаков.
Выбор первичных признаков базируется на обобщенном спектральном анализе, который в свою очередь, опирается на теорию среднеквадратической аппроксимации непрерывных функций в априорно выбираемых базисах в гильбертовом пространстве. Задача значительно упрощается при использовании ортонормированных базисных функций. Частными случаями ортонормированных базисов с единичным весом являются базисы, дающие разложение функций в ряд Фурье и в ряд Котельникова.
Поскольку блок принятия решения в настоящее время реализуется, как правило, на основе дискретной или цифровой обработки сигналов, то в качестве первичных признаков часто используются отсчеты сигналов в дискретном времени (по Котельникову) или дискретные числовые наборы.
Общая аналитическая зависимость входного сигнала без постоянной составляющей может быть представлена в виде
![]() ,
(5.1)
,
(5.1)
где
![]() огибающая;
огибающая;
![]() мгновенная
частота;
мгновенная
частота;
![]() случайная
фаза.
случайная
фаза.
Если информация о физических и механических признаках объектов заключена в статистических характеристиках огибающей, случайной фазы или мгновенной частоты и нестационарность входных сигналов в БЛ вызвана изменением во времени одного или нескольких из этих информативных признаков, то, как показано в гл. 4 , в АИС БЛ целесообразно не проводить обработку сигнала в целом, а выделять перечисленные вторичные информативные признаки. Эти признаки в общем случае представляют собой случайные нестационарные процессы, для которых априорно не известны математические ожидания, оценка последних часто не представляется возможной из–за высокого быстродействия систем. Отметим, что в АИС информация о мгновенной частоте и случайной фазе часто получается в результате обработки интервалов между нулями входных реализаций.
Важными вопросами при разработке АИС БЛ являются вопросы выбора информативных признаков и вопросы сокращения размерности векторов признаков.
Цель выбора информативных признаков сигналов состоит в выборе таких признаков, которые являются наиболее эффективными с точки зрения разделимости классов.
Теоретически наилучшим критерием эффективности информативных признаков является вероятность ошибки. На практике одним из наиболее распространенных критериев является вероятность ошибки, полученная экспериментально. Однако для критерия вероятности ошибки не существует явного математического выражения (даже в случае нормальных распределений вычисление вероятности ошибки требует численного интегрирования). Классическая теория распознавания образов оперирует с критериями разделимости классов, задаваемыми в явном виде. Поскольку разделимость классов зависит не только от распределений объектов в классах, но также и от используемого классификатора, то в классической теории рассматриваются критерии, оптимальные для байесовского классификатора, что позволяет минимизировать ошибку классификации. Тогда разделимость классов будет эквивалентна вероятности ошибки байесовского классификатора.
Помимо корректного выбора информативных признаков, важно также правильно определить размерность входного вектора признаков. Слишком малая размерность входного вектора может отрицательно повлиять на качество распознавания из-за потери информации, хранящейся в неучтенных коррелированных отсчетах. Тогда как слишком большая размерность входного вектора также может отрицательно повлиять на качество полученных алгоритмов, наоборот, из-за учета слабо коррелированных отсчетов.
В теории распознавания образов для выбора признаков и сокращения размерности векторов признаков широко используются [9,12,25] разложения Карунена–Лоэва, его дискретный аналог – метод главных компонент и метод множественного дискриминантного анализа. Эти методы оперируют центральными (ковариационными) моментами случайных отсчетов сигналов, последние два метода предполагают нахождение собственных векторов и собственных чисел по заданной ковариационной матрице.
В многоканальных системах БЛ часто информация о пространственно – геометрических и физических признаках объектов заключена в соотношениях между детерминированными составляющими параметров сигналов при каждом из конкретных условий встреч и задачи по построению АИС часто приходится решать условиях неизвестных математических ожиданий, поэтому применение перечисленных выше классических методов часто оказывается затруднительным.
Как показано в Гл. 3 в этих случаях наиболее наглядным и удобным оказывается применение аппарата начальных регрессионных характеристик, который, как будет показано далее, позволяет решать поставленные задачи и в условиях вырожденности или плохой обусловленности данных при неизвестных математических ожиданиях и ковариационных матрицах.
Применение регрессионных или нейросетевых алгоритмов в БЛ позволяет решать задачи обнаружения и распознавания при использовании в качестве признаков нецентрированных параметров сигналов. При этом необходимо рассмотреть вопросы обоснования критериев для выбора информативных признаков и сокращения размерности векторов признаков применительно к алгоритмам, использующим начальные оценки случайных параметров.
Рассмотрим однослойную нейронную сеть
(рис.5.1) , в которой каждый элемент из
множества входов
![]() отдельным весом соединен с каждым
искусственным нейроном, а каждый нейрон
выдает взвешенную сумму в сеть. Матрица
весов
отдельным весом соединен с каждым
искусственным нейроном, а каждый нейрон
выдает взвешенную сумму в сеть. Матрица
весов
![]() имеет
m строк и n столбцов, где m–число входов,
а n– число нейронов. Вычисление выходного
вектора
имеет
m строк и n столбцов, где m–число входов,
а n– число нейронов. Вычисление выходного
вектора
![]() ,
компонентами которого являются выходы
нейронов, сводится к матричному умножению
,
компонентами которого являются выходы
нейронов, сводится к матричному умножению
![]() .
(5.2)
.
(5.2)
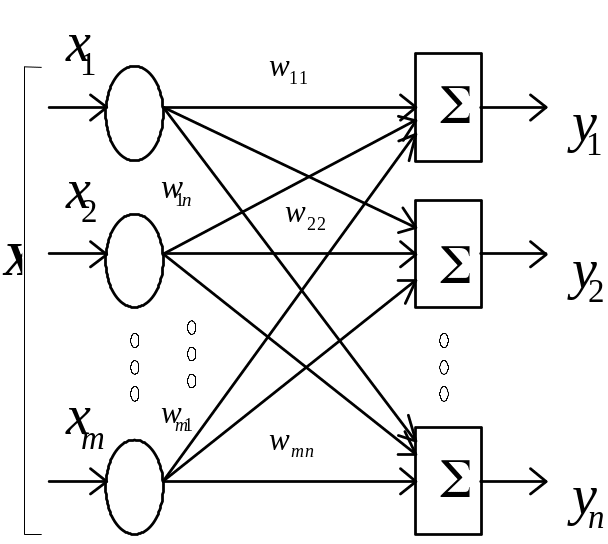
Рис. 5.1. Структурная схема однослойной нейронной сети без нулевых весов
Как видно из рис.5.1 при использовании в качестве входов (признаков) нецентрированных параметров сигналов в нейросети осуществляется обработка нецентрированных значений сигналов.
Исключим из рассматриваемой сети прямые
связи, т.е. положим ![]()
![]() i=1,2,.....,m и рассмотрим общий случай
сети с m нейронами.
i=1,2,.....,m и рассмотрим общий случай
сети с m нейронами.
Потребуем на каждом i–ом выходе нейрона
восстановления i–го входного сигнала
с минимальной ошибкой, т.е. в рассматриваемом
случае при обработке нецентрированных
параметров сигналов, с минимумом среднего
значения квадрата
![]() .
Произведем невырожденное преобразование
вектора
.
Произведем невырожденное преобразование
вектора
,
т.е. найдем матрицу так, чтобы остаточная сумма квадратов
![]() =
=![]() .
(5.3)
.
(5.3)
Дифференцируя остаточную сумму
квадратов
по
и приравнивая её нулю, для положительно
определённой и симметричной матрицы
начальных корреляционных моментов
![]() аналогично П.2.3 получим
аналогично П.2.3 получим
![]() ,
(5.4)
,
(5.4)
где
![]() .
.
Как следует из (4) весовые коэффициенты
![]() в рассматриваемом случае представляют
собой коэффициенты начальной регрессии
гл.2 , минимизирующие среднее значение
квадрата
на каждом выходе нейронной сети,
осуществляющей линейную обработку по
алгоритму
в рассматриваемом случае представляют
собой коэффициенты начальной регрессии
гл.2 , минимизирующие среднее значение
квадрата
на каждом выходе нейронной сети,
осуществляющей линейную обработку по
алгоритму
![]() .
.
В гл.3 рассмотрены оптимальные и квазиоптимальные алгоритмы обнаружения и распознавания случайных сигналов применительно к БЛ.
При обнаружении сигнала входная
реализация рассматривалась как аддитивная
смесь нормального нестационарного
случайного сигнала, заданного вектором
средних
![]() и матрицей ковариаций
и матрицей ковариаций
![]() , и полосового белого шума.
, и полосового белого шума.
При распознавании помеха задавалась аналогично сигналу и отличалась от последнего матрицей ковариаций и вектором средних. Вместо усреднения коэффициента правдоподобия по случайным параметрам предложено использовать оценки неизвестных случайных параметров, например на выходе линейного полосового фильтра.
При допущениях, справедливых для систем БЛ,
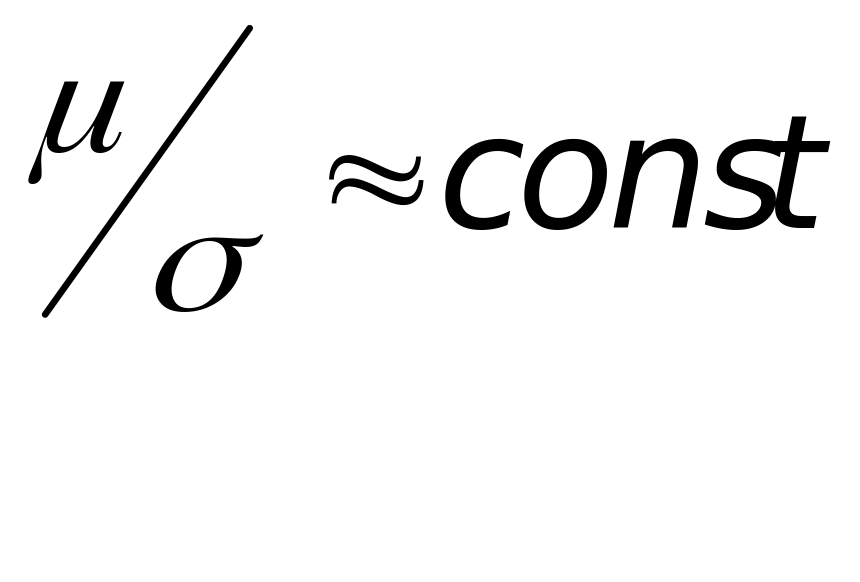 ,
,
![]() ,
,
квадратичные формы в алгоритмах обнаружения и распознавания сигналов могут быть представлены в виде:
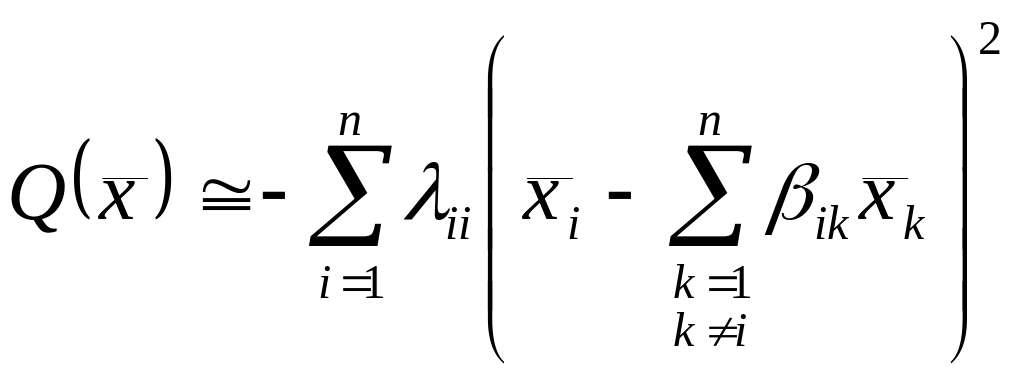 ,
(5.5)
,
(5.5)
где
![]() –
коэффициенты начальной регрессии;
–
коэффициенты начальной регрессии;
![]() –
оценки нецентрированных параметров
сигналов.
–
оценки нецентрированных параметров
сигналов.
Вычисляя условные плотности распределения
вероятностей для нормально распределенного
вектора, можно показать [1], что
![]() в (5.5) представляют собой величины,
обратно пропорциональные остаточным
дисперсиям множественных регрессионных
представлений
в (5.5) представляют собой величины,
обратно пропорциональные остаточным
дисперсиям множественных регрессионных
представлений
![]() .
.
В гл.2 начальная множественная регрессия определена как
![]()
где
![]() ;
;
– матрица корреляционных моментов;
;
;
– матрица корреляционных моментов;
![]() .
.
При допущениях, справедливых для систем БЛ,
, , и переходе к начальным моментам оценок случайных величин алгоритмы обнаружения и распознавания будут иметь вид :
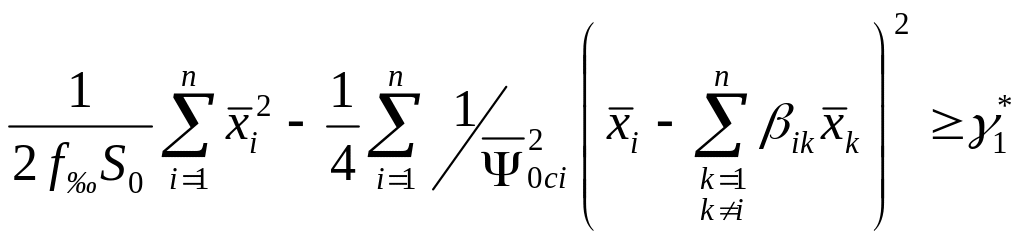 ,
(5.6)
,
(5.6)
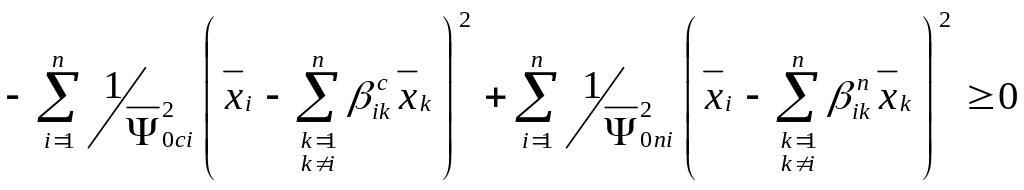 ,
(5.7)
,
(5.7)
где
![]() и
и
![]() –
остаточные средние оценок случайных
параметров соответственно для сигнала
и помехи.
–
остаточные средние оценок случайных
параметров соответственно для сигнала
и помехи.
На основании (5.5), (5.6) и (5.7) записаны через
остаточное среднее значение квадрата
![]() множественного начального регрессионного
представления. Как видно из (5.6) и (5.7) в
алгоритмах вычисляются отношения
квадрата ошибки множественных
регрессионных представлений координат
случайного входного вектора к
соответствующим остаточным средним
значениям квадратов
.
множественного начального регрессионного
представления. Как видно из (5.6) и (5.7) в
алгоритмах вычисляются отношения
квадрата ошибки множественных
регрессионных представлений координат
случайного входного вектора к
соответствующим остаточным средним
значениям квадратов
.
При переходе к линейным границам в главе 2 получены регрессионные алгоритмы (5.6) и (5.7) могут быть приведены к виду:
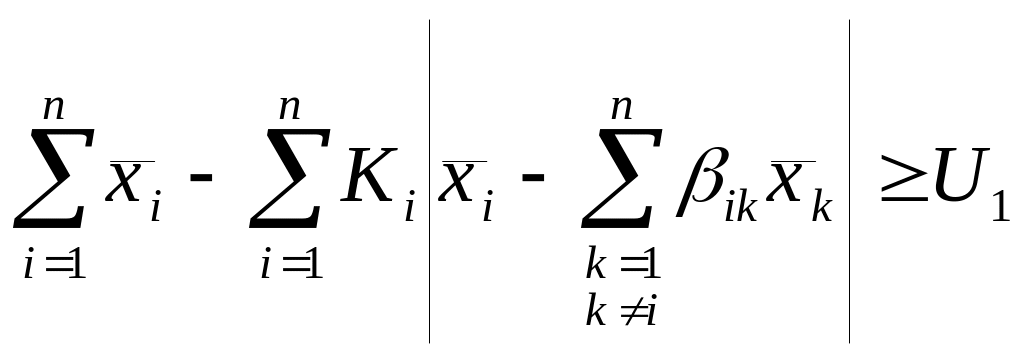 ,
(5.8)
,
(5.8)
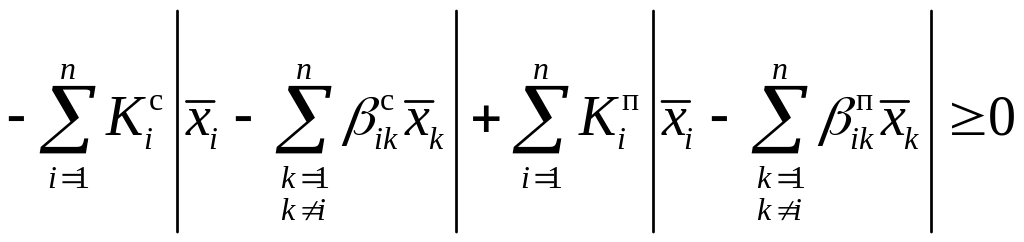 .
(5.9)
.
(5.9)
В главе 2 показано, что регрессионные алгоритмы имеют наглядный геометрический смысл, в них ограничивается относительное расстояние от линии начальной регрессии. В [ 14 ] отмечается, что алгоритмы, имеющие наглядный геометрический смысл могут применяться независимо от закона распределения входного вектора (при одномодальных распределениях).
Рассмотрим регрессионный алгоритм обнаружения и распознавания двумерного входного вектора
![]() , (5.10)
, (5.10)
где a и b – весовые коэффициенты.
Как видно из неравенства (5.10) (см.П.3.5), выбором коэффициентов a, b и K можно задавать положение линейных границ области принятия решения относительно линии регрессии, определяемой уравнением:
![]() .
.
Действительно, неравенство (5.10) можно заменить эквивалентной системой неравенств:
 (5.11)
(5.11)
Как видно из (5.11) и рис. 3.6 двухканальный регрессионный алгоритм можно реализовать с помощью двухслойной нейронной сети с пороговыми активационными функциями, где первый слой реализует неравенства (5.11), а второй слой, состоящий из одного нейрона, реализует операцию И (рис. 5.2). Параметры сети:
– матрица весов 1-го слоя ![]() ;
;
– вектор порогов 1-го слоя ![]() ;
;
– вектор весов 2-го слоя ![]() ;
;
– порог 2-го слоя ![]() .
.


Рис.5.2. Функциональная схема двухслойной нейронной сети, реализующей
