Среднеквадратическое отклонение оценки

.

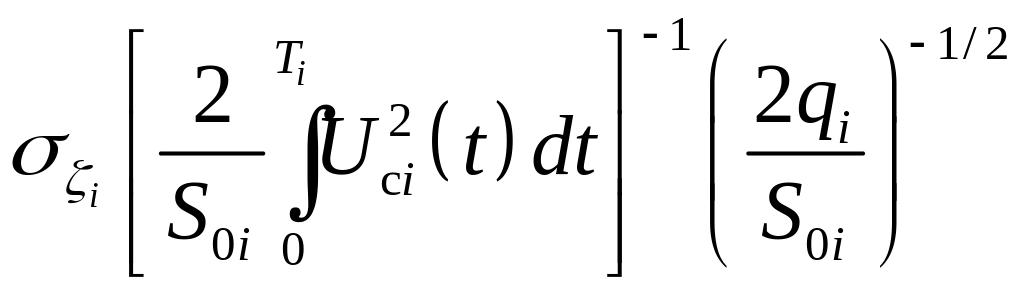Тогда относительную дисперсию оценки случайной амплитуды получим в виде

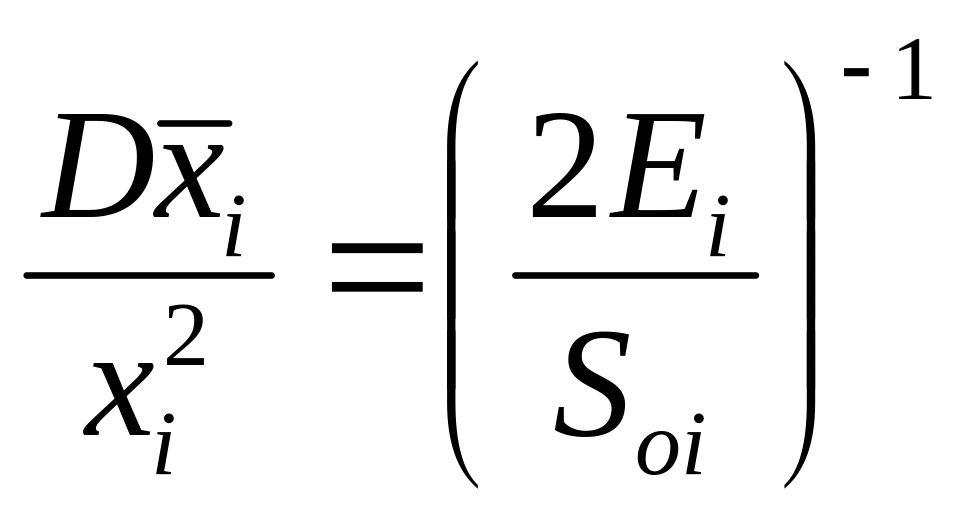, (3.21)

где 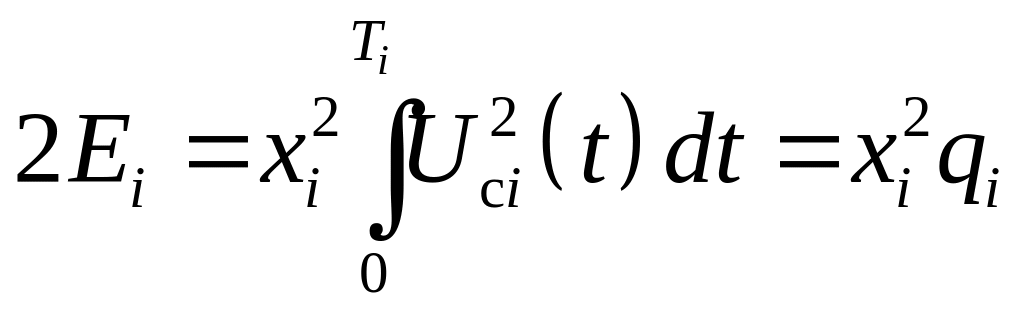– энергия принятого сигнала.

Из равенства (3.21) видно, что относительная дисперсия оцен­ки амплитуды сигнала, известного точно по форме, обратно про­порциональна удвоенному отношению энергии принятого сигнала к спектральной плотности шума.

Для больших отношений сигнал / шум с учетом уравнения (3.20) последние два члена в правой части выражения (3.17) мож­но вычислить, используя оценки случайных амплитуд на выходах оптимальных линейных фильтров, согласованных с единичными сигналами:

. (3.22)

Тогда при принятых допущениях алгоритм принятия решения (3.17) можно привести к виду

. (3.23)

Рассмотрим случай, когда многоканальная система решает за­дачу распознавания. На вход системы могут поступать реализа­ции, содержащие полезные сигналы (3.8) или помеху

, (3.24)

где – единичный сигнал помехи, известный точно; – его случайная амплитуда.

При нормальном законе распределения случайных амплитуд помехи аналогично выражению (3.9) имеем

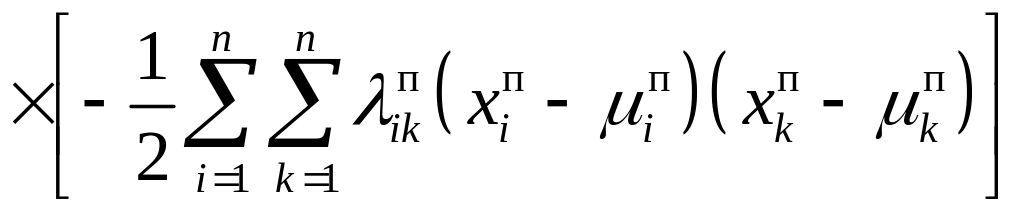. (3.25)

Коэффициент правдоподобия представим в виде

, (3.26)

где – коэффициент правдоподобия гипотезы о наличии на входе сигнала на фоне шума, определяемый левой частью вы­ражения (3.16); –коэффициент правдоподобия гипотезы о наличии на входе помехи на фоне шума.

Тогда на основании выражений (3.16), (3.17), (3.23) и с уче­том равенства (3.26) решение о наличии полезного сигнала на входе системы распознавания можно принимать:

, (3.27)

где

. (3.28)

В равенстве (3.28) индексом «с» обозначены параметры полез­ного сигнала, а индексом «п» – помехи.

В тех случаях, когда система должна решать как задачи обна­ружения, так и задачи распознавания, решение о наличии полезного сигнала на входе системы должно приниматься при совмест­ном выполнении неравенств (3.17) и (3.27).

Если формы сигналов и помех в каждом канале совпадают, т. е.

,

то оценки случайных параметров сигналов и помех мож­но производить на выходах одних и тех же фильтров, согласован­ных с единичными сигналами . Тогда на основании неравен­ства (3.27) при решении задачи распознавания необходимо вычис­лять неравенство

. (3.29)

3.3. Алгоритмы работы квазиоптимальных систем обнаружения и распознавания случайных процессов.

Рассмотрим задачу обнаружения нестационарного случайного процесса на интервале времени Т в аддитивной смеси с белым шумом, не коррелированным с сигналом. Тогда выбороч­ная реализация процесса на входе системы

. (3.30)

Нестационарные нецентрированные реализации могут подвер­гаться дискретизации в предположении, что спектр каждой выбо­рочной реализации ограничен частотой среза . Тогда при разло­жении нестационарных реализации по ортогональным координа­там целесообразно воспользоваться приближенным разложением по Котельникову и представить каждую выборочную реализацию отсчетами.

При решении задач обнаружения и принятых допущениях мож­но не рассматривать полосу частот вне интервала 0– и считать шум полосовым белым, ограниченным верхней частотой . Тогда плотность распределения вероятностей шума будет записываться аналогично выражению (3.10), так как отсчеты случайного процес­са с постоянной спектральной плотностью в ограниченной полосе 0– взятые по Котельникову с интервалом , оказываются некоррелированными, т. е. имеют диагональную матрицу корреля­ционных моментов. Отсчеты нестационарного сигнала , представленного по Котельникову:

, (3.31)

в общем случае будут коррелированными. Тогда сигнал может быть задан вектором средних 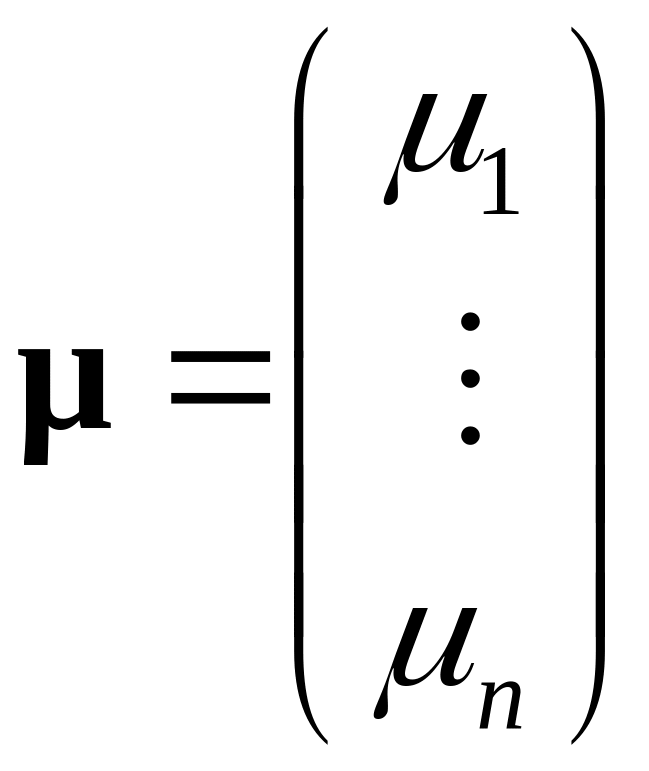и матрицей ковариационных моментов и при нормальном распределении отсче­тов плотность распределения вероятностей будет иметь вид выражения (3.9).

Для входного случайного процесса , представленного по Котельникову, можно воспользоваться методами, рассмотрен­ными в П. 3.2, т. е. полагать, что на вход системы поступает сово­купность ортогональных сигналов , известных точно по форме и имеющих случайные коррелированные амплитуды , в смеси с белым полосовым шумом.

Для рассматриваемого случая:

; (3.32)

, (3.33)

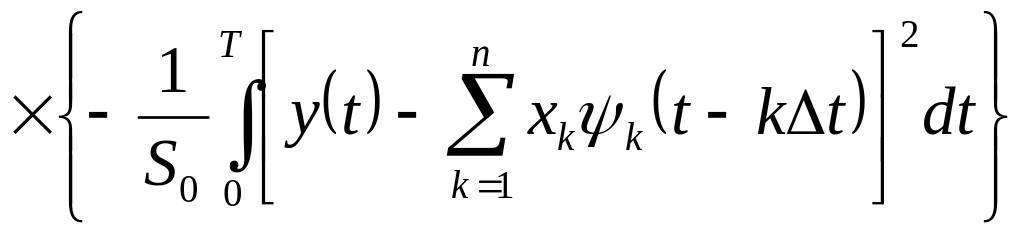; (3.34)

(3.35)

и определяется выражением (3.10). Тогда на основании выраже­ний (3.9), (3.10), (3.32)–(3.35) коэффициент правдоподобия (3.11) можно представить в виде

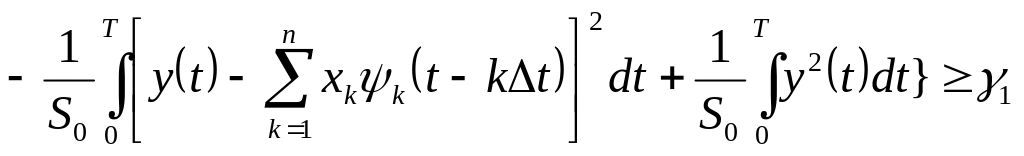. (3.36)