Глава 3. Алгоритмы систем обнаружения и распознавания сигналов в условиях априорной неопределенности

3.1. Возможные методы решения задач обнаружения и распознавания сигналов в ближней локации

К задачам теории оптимального приема сигналов относятся об­наружение и распознавание сигналов, оценка параметров и фильт­рация сигналов, анализ прохождения случайного сигнала по кана­лу с заданными характеристиками. Особенностью задач в ближней локации является случайная природа и нестационарность ис­точника сообщения и мешающих воздействий, чем и объясняется эффективность статистического подхода к их решению. Подход за­ключается в том, что для отыскания решения задачи должны быть заданы статистические (вероятностные) модели сигналов и помех и статистический критерий оптимальности решения. Однако воз­можны различные методы решения проблемы, которые разделяют­ся на структурные и неструктурные.

Структурные методы обработки сигнала характеризуются сле­дующими основными особенностями. При структурном подходе не­обходимо задание класса устройств обработки сигнала, удовлетво­ряющих, например, требованию, чтобы эти устройства были линей­ными фильтрами с неизмененными во времени параметрами. Не­обходимо выбрать наилучшую (по принятому критерию) систему в данном классе. Выбор наилучшей в рамках заданного класса системы производится по определенному критерию, например по критерию максимума отношения сигнал / шум.

При структурном подходе используются структурные модели сигнала, которые в общем случае определяются как связи по пра­вилу Ф{…..} в двух или более временных зависимостях сигна­ла, его производных, интегралов или его линейных преобразова­ний. Выражение для структурной связи сигнала в общем случае имеет вид

, (3.1)

где – принятое колебание; – линейное преобразо­вание .

Смысл использования структурной модели сигнала заключает­ся в том, что при надлежащем выборе вида преобразования Ф в выражении (3.1) можно освободиться от избыточной ин­формации или от влияния непостоянства безынформационных па­раметров, т. е. достичь инвариантности относительно них. С этим связано одно из достоинств структурного подхода к решению ста­тистических задач, заключающееся в том, что для его применения обычно достаточно частичного описания (задания) сигналов. На практике требуемые параметры приходится измерять или рассчи­тывать, поэтому это преимущество существенно.

К преимуществам структурного способа обработки сигналов следует отнести также возможность в каждый момент времени разделить траектории измеряемых информативных параметров. Вследствие этого сложные в техническом отношении устройства памяти, присущие корреляционным системам, не являются необ­ходимыми элементами систем при структурном подходе.

Существуют, однако, моменты, ограничивающие возможности структурного подхода при решении статистических задач оптими­зации. Одним из недостатков структурного метода является то, что выбор структурной связи, задающей по существу структуру системы обработки сигнала, в каждом случае определяется в значительной степени интуицией исследователя, и часто невозможно заранее определить, правильно ли выбрана структура. В частнос­ти, при решении задачи простая нелинейная система может заведо­мо превосходить лучшую линейную систему. Попытка решить про­блему выбора надлежащей структуры путем предположения, что она является произвольной нелинейной системой с изменяющими­ся во времени параметрами, оказывается несостоятельной из-за того, что не существует приемлемого метода исследования всех возможных систем, если опираться на структурный подход.

При оценке возможностей структурных методов построения си­стем принятия решения в ближней локации необходимо учитывать следующее:

1. При формировании структурных моделей сигналов наиболее часто используемыми его контурными моделями являются сигнал и его производные. В системах ближней локации рабочие сигналы имеют большой динамический диапазон изменения амплитуд и час­тот, а операции дифференцирования первого порядка и более вы­соких увеличивают динамику сигнала, циркулирующего в системе, усложняя ее техническую реализацию.

3. Поскольку в системах ближней локации мешающие воздей­ствия могут на 60 дБ и более превышать полезный сигнал, то для обеспечения линейности тракта обработки (с целью исключения подавления полезного сигнала) необходимо на входе системы осу­ществлять спектральную селекцию принятого колебания. Такое преобразование в большинстве случаев искажает форму сигналов, что создает трудности для применения в этих условиях структур­ных методов.

3. Сигналы и помехи в системах ближней локации часто могут совпадать по форме и отличаться только диапазоном изменения па­раметров, например, параметра сигнала экспоненциальной формы

.

Это обстоятельство затрудняет применение структурных мето­дов построения систем, реагирующих на сигналы определенной формы и инвариантных к остальным параметрам сигнала.

4. В большинстве работ не используются различия в корреляци­онных свойствах сигналов и помех, поэтому процедуры обработки сводятся к дисперсионной, а не корреляционной обработке сигналов.

5. В случае одиночных сигналов заданной формы структурные методы могут упростить техническую реализацию системы. Осо­бенно перспективно применение в системах ближней локации структурно-сигнальных параметрических фильтров, например при фильтрации ЧМ – колебаний.

Альтернативой структурного подхода служит неструктурный ме­тод, при котором не делают априорных предположений относи­тельно структуры устройства обработки сигналов, а задают кри­терии, находят алгоритм и реализуют полученную процедуру обработки. Преимуществом этого метода является то, что найденная структура устройства обработки – наилучшая (с точки зрения выбранного критерия) из всех возможных.

Недостаток неструктурного подхода заключается в том, что не­обходимо полностью характеризовать (задавать) все сигналы, ка­налы и помехи, относящиеся к задаче. Однако существует большое число практически важных задач, в которых такое полное задание возможно.

Неструктурные методы – это методы оптимальных решений, позволяющие оценить наилучшие (возможные с точки зрения выб­ранного критерия) характеристики системы обработки сигнала. Особенностью большинства оптимальных систем является наличие устройства памяти, позволяющего использовать для принятия ре­шения информацию, заложенную в корреляционных связях пара­метров сигналов и помех.

В классической постановке рассматривается обнаружение (рас­познавание) нормального стационарного центрированного случайного сигнала в аддитивной смеси с некоррелированным нормальным шумом, причем корре­ляционные свойства обоих процессов предполагаются заданными матрицами ковариационных моментов и соответст­венно для сигнала и шума.

Для задачи обнаружения сигнала в реализации коэффициент правдоподобия имеет вид

, (3.2)

где

; (3.3)

и – отсчеты входной реализации ;

; ; ;

N – объем выборки.

Из выражения (3.3) видно, что для случайного сигнала опти­мальный обнаружитель по статистическим и информационным кри­териям является нелинейным устройством, осуществляющим весо­вое суммирование произведений значений выборки входного цент­рированного процесса.

Одним из способов реализации алгоритма

(3.4)

является применение дискретно-аналогового фильтра или дискрет­но-аналогового преобразователя, устройства задержки, процессора и арифметического устройства.

В системах ближней локации оптимальные системы, как пра­вило, не реализуемы из-за технической сложности. В целях упрощения системы обнаружения (распознавания) предполагается час­то парная корреляция в двух соседних отсчетах, сдвинутых по вре­мени на время , тогда правило решения (3.4) будет иметь вид

, (3.5)

где

; .

Алгоритм (3.5) часто сводят к вычислению оценки нормиро­ванного коэффициента корреляции и сравнению ее с постоян­ным порогом

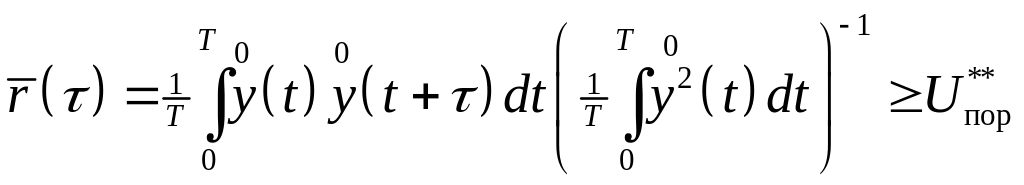. (3.6)

Для реализации алгоритмов (3.5) и (.3.6) используют корреля­торы, дозволяющие получить оценки автоковариационных момен­тов,

. (3.7)

Чаще всего применяются корреляторы мультипликативного ти­па, основной операцией которых является перемножение текущего отсчета реализации и задержанного на .

Недостаток корреляционных систем рассмотренного типа– сложность технической реализации быстродействующих перемно­жающих устройств, работающих в широком динамическом диапа­зоне входных сигналов. В реальных перемножающих устройствах аналогого типа происходит не только перемножение, но и де­тектирование сигналов. Детектирование приводит к появлению по­стоянной составляющей напряжения на выходе перемножителя, которая не связана с наличием корреляции между входными про­цессами и зависит от нестабильности питающих напряжений.

При нестационарных входных сигналах и нестабильных питаю­щих напряжениях постоянную составляющую детекторного эффек­та не удается исключить с помощью компенсационного напряже­ния. Решение задач может быть упрощено применением функцио­нальных корреляторов, в которых вместо непрерывного перемно­жения входных процессов осуществляется перемножение функций этих процессов. К функциональным корреляторам в зависимости от вида функционального преобразования относятся корреляторы разностной частоты, цифровые – при конечном числе N уровней квантования; знаковые – при N=2; релейные – когда знаковому преобразованию подвергается один из входных сигналов.

В системах ближней локации при оценке корреляционных функций случайных процессов цифровыми и знаковыми методами следует учитывать погрешности от шумов кванто­вания. Методы вычислительной техники позволяют реализовать цифровые корреляторы в заданных габаритах при помощи аналого-цифрового преобразователя, устройства задержки и арифмети­ческого устройства, однако последние часто не обеспечивают тре­буемые быстродействие и динамику.

Следует отметить общие особенности корреляционных методов обработки сигналов, ограничивающих их применение в системах ближней локации. При корреляционных методах исследуются центральные смешанные моменты второго порядка, которые ха­рактеризуют корреляционные свойства центрированных частей случайных процессов. В системах ближней локации нестационар­ность сигналов, обусловленная изменением во времени априорно неизвестных математических ожиданий, не позволяет оценить пос­ледние на интервале принятия решения с достаточной точностью и, следовательно, провести корреляционные измерения рассматривае­мыми способами.

При обработке в корреляционных системах центрированных сигналов, нестационарность которых обусловлена изменением во времени средней частоты энергетического спектра, необходимы устройства автоматического слежения за задержкой сигнала, ко­торые требуют время на самонастройку, соизмеримое с заданным временем принятия решения в системах ближней локации.

Кроме того, в системах ближней локации информация о прост­ранственно-геометрических признаках объектов и помех может быть заключена в функциональной связи детерминированных со­ставляющих нестационарных входных процессов. Поэтому для при­нятия решения в подобных случаях целесообразно использовать вторые смешанные начальные моменты. Одним из путей решения задач, учитывающих специфику систем ближней локации, являет­ся использование регрессионных методов обработки сигнала, позволяющих реализовать априорную информацию о корреляционных связях информативных параметров сигналов с помощью простых операций весового суммирования и детектирования. При использо­вании регрессионных методов информация о корреляционных свой­ствах нестационарных процессов может быть получена с помощью знаковых функциональных преобразований сигналов. При этом отпадает необходимость в автоматических устройствах, следящих за задержкой, и не требуется время на самонастройку. Регрессион­ный способ может быть использован для извлечения информации о функциональных связях между детерминированными составляю­щими нестационарных процессов даже при отсутствии ковариации и допускает перестройку области принятия решения в адаптивных системах.

Регрессионные системы в большинстве случаев нечувствитель­ны к изменению питающих напряжений, однако в многоканальных системах требуют стабильности коэффициентов передачи трактов.