1.3 Задача про заміну устаткування без урахування залишкової вартості устаткування

Постановка задачі. Нехай r(t) - вартість продукції, виробленої за рік на одиниці устаткування, вік котрого t років; L(t) – щорічні витрати на обслуговування цього устаткування; S(t)=0 – залишкова вартість устаткування; Р=11грош. один. – вартість нового обладнання. Уведемо функцію φ(t)=R(t)-L(t), різниця між вартістю виготовленої продукції та експлуатаційних витрат. Значення функціі φ(t) за роками наведені у таблиці 10.

Таблиця 10

Значення функції φ(t) за роками

t	0	1	2	3	4	5	6
φ(t)	13	12	11	10	9	8	7

Визначити оптимальний цикл заміни устаткування за період часу тривалістю шість років, причому за ці роки прибуток f₆(t), повинен бути максимальним.

Розв΄язок. Функціональне рівняння Беллмана:

прибуток .

Умови заміни:

;

.

Усі обчислення проведемо за формулами для різних N=1,…..,6:

;

;

;

;

;

.

Результати обчисленнь проведемо в таблиці 11.

Таблиця 11

Результати обчислень значень функції .

		1	2	3	4	5	6
	13	12	11	10	9	8	7
	25	23	21	19	17	15	---
	36	33	30	27	25
	46	42	38	35	35
	55	50	46	45	44	44
	63	58	56	54	53	52	---

Висновки. Якщо спочатку обладнання нове ( ), то за шість років роботи прибуток складе 63 грошові одиниці. Причому заміна обладнання не виконується.

1.4 Задача про заміну устаткування з урахуванням залишкової вартості устаткування

Постановка задачі. Нехай r(t) – вартість продукції, виробленої за рік на одиниці устаткування, вік котрого t років; L(t) – щорічні витрати на обслуговування цього устаткування; S(t) – залишкова вартість устаткування; Р(t) – вартість нового обладнання.

Уведемо функцію φ(t)=R(t)-L(t) – різниця між вартістю виготовленої продукції та експлуатаційних витрат. Значення функції φ(t) за роками наведені у таблиці 11.

Нехай S=Р(t)-S(t)=40 грош. один..

Таблиця 11

Значення функціі φ(t) за роками

t	0	1	2	3	4	5	6	7
φ(t)	60	55	35	30	23	5	0	0

Визначити оптимальний цикл заміни устаткування за період часу тривалістю сім років, причому за ці рокиприбуток f₇(t), повинний бути максимальний.

Розв΄язок. Нехай f_n(t) – максимальний прибуток за N етапів експлуатації устаткування, якщо устаткуванню t років.

Зв'язок років і етапів поданий у вигляді:

Тоді функціональні рівняння Беллмана мають вигляд:

,

N=1,…,7.

Усі обчислення робимо в таблиці 12 для різних N:

N=1, ;

N=2, ;

N=3, ;

і так далі.

Таблиця 12

Результати обчислень значень функції .

t	0	1	2	3	4	5	6	7
f1(t)	60	55	35	30	23	20	20	20	20
f2(t)	115	90	75	75	75	75	75	75	20+55
f3(t)	150	130	110	110	110	110	110	110	20+90
f4(t)	190	165	150	150	150	150	150	150	20+130
f5(t)	225	205	185	185	185	185	185	185	20+165
f6(t)	265	240	225	225	225	225	225	225	20+205
f7(t)	300	280	260	260	260	260	260	260	20+240

Висновки. За сім років при використанні в перший рік нового обладнання (t=0) максимальний прибуток становитиме f₇(0)=300 грош. один.. При цьому наприкінці третього року треба поміняти устаткування, а потім – провести заміну наприкінці п'ятого року роботи устаткування.

Задача 2.1 С М О із відмовами

На переговорній станції є чотири лінії зв'язку. Виклик, що надходить, коли всі лінії зайняті, одержує відмову. Інтенсивність потоку викликів викл./хв. Середня тривалість розмови – хв. Усі потоки, заявок і обслуговування найпростіші. Знайти:

1) характеристики системи , ;

2) імовірності станів P_к;

3) абсолютні й відносні пропускні спроможності , ;

4) середнє число зайнятих ліній ;

5) середній час простою одного каналу , де ймовірність зайнятості ;

6) знайти економічну ефективність роботи станції, якщо 1 хв простою лінії завдає збитку грн /хв , а роботи – прибуток грн/хв, ефективність лінії, , а ефективність телефонної станції ; n – число ліній, N=12 годин, тривалість робочого дня.

Розв΄язок.

1. Знайдемо характеристики системи , .

2. Імовірність станів:

Р=1+2,2+2,42+1,775+0,976=8,371;

; ;

; ; .

3. Імовірність відмови: , імовірність обслуговування заявки: .

4. Середнє число зайнятих каналів .

5. Відносна пропускна спроможність .

Абсолютна пропускна спроможність: .

6. Середній час простою одного каналу:

; хв.

7. Економічна ефективність роботи станції за одну хвилину:

грн./хв.

Економічна ефективність роботи станції протягом дня:

грн /день

Висновок.

При сталому режимі роботи телефонної станції в середньому працюють два канали з чотирьох. Обслуговується лише 88% заявок, які надходять, що дає прибуток у розмірі 10 к/хв. Це складає 290,88 грн за добу. З цього випливає, що станція працює недостатньо ефективно. Керівництву необхідно визначити, що впливає на низьку ефективність роботи більшою мірою: простій лінії або недостатньо високий відсоток обслуговування заявок, що, у свою чергу, впливає на прибуток.

Задача 2.2 С М О з обмеженою чергою

На станцію поточного ремонту автомашин надходить у середньому маш/год, потік заявок найпростіший. Є два ґаражі для ремонту. На подвірї станції можуть знаходитися одночасно ≤ машини, що очікують черги. Середній час ремонту однієї машини – t_об.=2,6 год. Визначити прибуток роботи станції за добу (12 годин), якщо:

1) година роботи ґаража коштує 34 грн ;

2) за діагностику кожної машини, що ремонтується, беруть 20 грн;

3) година роботи кожного майстра з бригади з двох чоловік, що обслуговують ґараж , коштує 3,1 грн, простою – 1,1 грн ;

4) податки складають 40% від заробленої суми;

5) інші витрати у середньому 20 грн з ґаража за добу.

Визначити економічну доцільність уведення в експлуатацію ще одного ґаража, якщо його вартість 10000 грн.

Прибуток станції знаходиться      ,

де ; ; ; ;        ;

Розв΄язок.

1. Знайдемо характеристики системи :

; ; –тривалість робочого дня.

2.Знайдемо імовірності станів без черги:

_Р0=(2,34⁰_{/0! + 2,34}¹_{/1! + 2,34}²_{/2! + 2,34}²_/2!·((1,17⁵_{-1,17)/(1,17-1)))}^-1₌

=(1+2,34+2,74+2,74·((2,192-1,17)/0,17))^-1=22,56^-1=0,044.

;

;

.

Відносна пропускна спроможність .

Середній час роботи 2-х ґаражів:

Абсолютна пропускна спроможність, середнє число обслуговуваних машин:       .

Імовірність зайнятості ґаража:

,

де середнє число зайнятих ґаражів – ґаражів,

.

Імовірність простою:

.

Ефективність роботи двох ґаражів:

 

      

=252грн/добу.

ІІ. Визначимо економічну доцільність уведення в експлуатацію ще одного ґаража , коли працють три ґаража, .

1. Характеристики системи ті ж самі, що і при :

,       , окремо

2. Знайдемо ймовірності станів без черги.

Усі ґаражі не працюють:

_Р0=(2,34⁰_{/0! + 2,34}¹_{/1! + 2,34}²_{/2! +2,34}³_{/3! + 2,34}³_/3!·((0,78⁵_{-0,78)/(0,78-1)))}^-1₌

= .

Працює один ґараж :

.

Працюють два ґаражі:

.

Працюють три ґаражі:

.

;

, .

Середній час роботи трьох ґаражів:

=24,18 год.

Середнє число обслуговуваних машин:

.

Середнє число зайнятих ґаражів:

.

Імовірність зайнятості ґаража:

.

Імовірність простою ґаража:

.

Ефективність роботи трьох ґаражів:

=441,88 грн/добу.

Економічна ефективність від уведення третього ґаража:

Термін окупності:

Висновок: при даному режимі роботи обслуговується 8,352 машини за день, що приносить прибуток у розмірі 252 грн за один робочий день.

При введенні третього ґаража число машин, що обслуговуються, збільшилося б до 10,14 машини, збільшився б також середній час роботи

ґаражів - 24,18 час. Це, в свою чергу викликало б збільшення прибутків на

189,88 грн на день. Строк окупності 3-го ґаража склав 52,6 діб.

Проект побудови 3-го ґаража ефективний. Необхідно прийняти рішення про будівництво.

Задача 2.3 С М О із необмеженою чергою

Фірма, що забезпечує зв'язком журналістів, які освітлюють міжнародну конференцію, має три лінії супутникового зв'язку. Потік заявок найпростіший зы щільністю 0,24 заявок/хв.. Середній час передачі повідомлення хв /заявок, випадкова величина, що має показовий розподіл.

Журналіст зобов'язаний передати повідомлення якомога раніше у своє агентство або газету. Знайти прибуток фірми за добу (24 години), якщо хвилина розмови коштує у середньому 3,2 дол./хв, а за час чекання в черзі фірма сплачує клієнтові компенсацію 1,13 дол /хв .

Визначити доцільність запровадження ще однієї лінії зв'язку, якщо її вартість 5000 дол, а конференція триває три дні.

Прибуток фірми розраховується за формулою:

дол,

де сумарний час заняття каналів , число заявок за добу , сумарний час очікування , доцільність запровадження ще однієї лінії зв'язку , де П₄ - прибуток за добу при n=4.

Розв΄язок.

Початкові умови: лінії зв’язку; заявок/хв; хвилин;

– вартість одної хвилини розмови; – компенсація.

1) Характеристики системи: – середнє число заявок.

2) – черга не накопичується, система стала.

3) – середнє число зайнятих каналів.

4) , , число заявок, що обслуговуються за добу:

Імовірність відсутності повідомлень:

.

5) хвилин очікує один клієнт.

6) (хвилин) – час очікування за добу всіх клієнтів.

7) - час обслуговування всіх клієнтів за добу.

8) $ - прибуток фірми при трьох лініях зв’язку.

Якщо число ліній зв’язку :

– черга не накопичується – стан сталий;

Імовірність відсутності повідомлень:

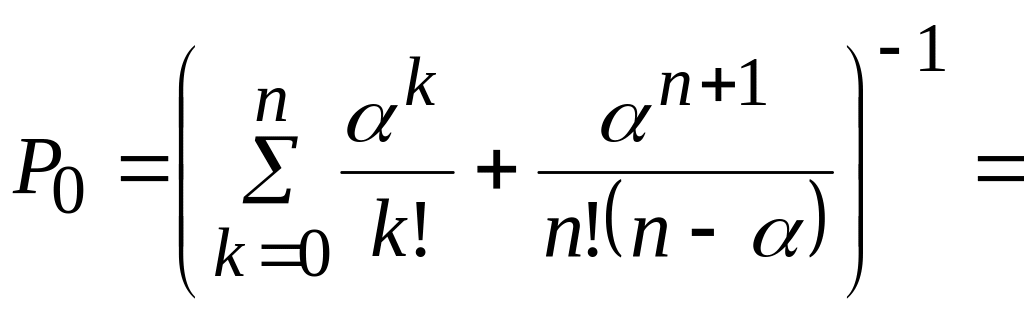(2,04⁰/0!+ 2,04¹/1!+2,04²/2!+2,04³/3!+2,04⁴/4!+

+2,04⁵/4!/(4-2,04))^-1 ;

хвилин;

;

;

=9088,68 дол.;

.

Висновок: при функціонуванні трьох ліній супутникового зв’язку фірма отримує прибуток у розмірі 7795,3 дол/добу.

При введенні четвертої лінії зв’язку на час самміту (три доби) фірма отримає додатково 3880,14 $.Порівняно із витратами, необхідними для введення в експлуатацію четвертої лінії, це недостатньо. Тому проект невигідний.

Якщо б самміт тривав би довше, то й додатковий прибуток був би вищим. За таких умов необхідно переглянути рішення про введення в експлуатацію четвертої лінії зв’язку.

Задача 3.1 Розв΄язати аналітично та графічно гру, що задана матрицею платежів

Розв΄язати гру, якщо платіжна матриця має вигляд

6	-1	-3
0	4	5

Розв΄язок Як прямуе із платіжної матриці, таблиця 13, виграші 1-го гравця

виграші 2-го гравця

- немає сідлової точки, рішення шукаємо серед змішаних стратегій.

Графічне розв΄язання гри для гравця А

Для трьох стратегій гравця В знаходимо виграш гравця А при застосуванні гравцем А змішаної стратегії , де - ймовірність застосування стратегії , і=1;2.

Таблиця 13

Платіжна матриця з цінами гри для вибраних

стратегій гравців ,

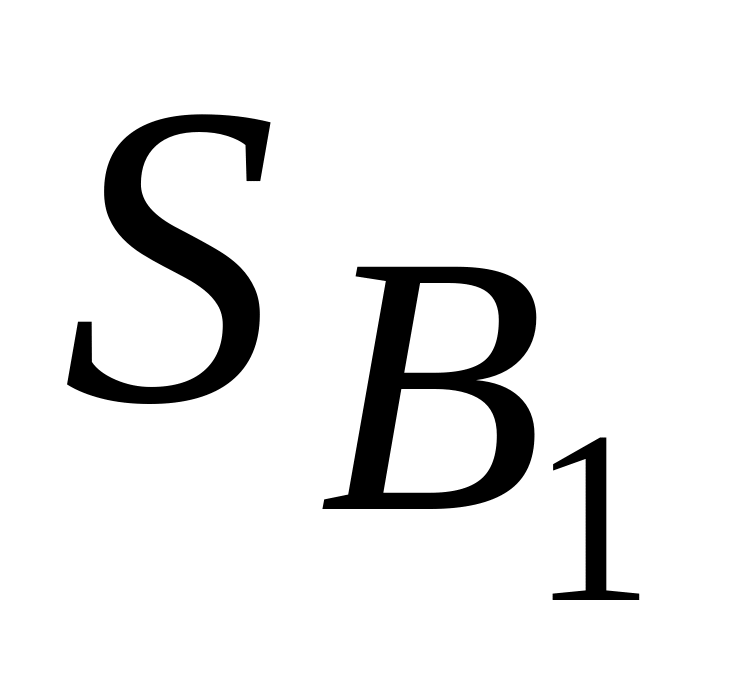
	6	-1	-3	-3
	0	4	5	0
	6	4	5

Рис. 3.1– Графічне розв΄язання гри для гравця А

Виразимо через . Імовірність повної групи подій :

,

будуємо ці прямі Vi, і=1; 2; 3, за двома точками на осях Х₁ та V, рис. 3.1. Необхідні розрахунки проведені у таблиці 14.

Відкидаємо ту пряму (стратегію), яка не проходить через точку оптимуму . Це пряма , яка відповідає стратегії гравця В, .

Якщо проходять усі три, то відкидаємо одну з двох, що мають однаковий нахил.

Таблиця 14

Точки перетину прямих з осями

Х1 V	0	1
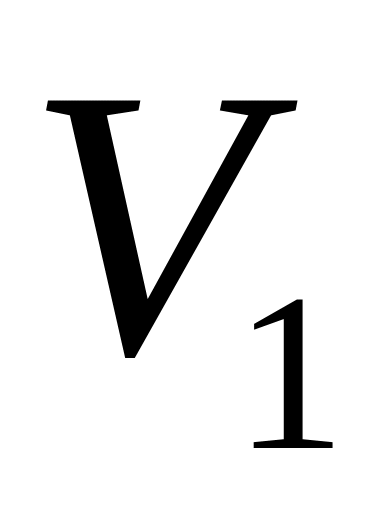
	0	6
	4	-1
	5	-3

Висновок. Як випливає з рисунка 3.1, оптимальна змішана стратегія гравця А:

зі імовірністю застосовувати стратегію ,а потімзі імовірністю

застосовувати стратегію У результаті застосування оптимальної змішаної стратегії гравцем А його виграш складає грош. один.

Знайдемо графично оптимальну змішану стратегію гравця В.

Імовірність застосування гравцем В відкинутої стратегії дорівнює нулю, тобто . Для гравця В залишилося 2 стратегії. Для двох стратегій гравця А знаходимо програш гравця В при застосуванні гравцем В змішаної стратегії , де – ймовірність застосування стратегії , j=1;3, причому у₁+у₃=1.

Розв'язуємо задачу графічно для двох стратегій , .

Будуємо ці прямі W₁,W₃ за двома точками на осях У₁ та V. Необхідні розрахунки проведені у таблиці 15.

Висновок. Як випливає з рисунка 3.2, оптимальна змішана стратегія гравця В:

зі ймовірністю застосовувати стратегію ,а потім – зі імовірністю

Таблиця 15

Точки перетину прямих з осями

У1 W	0	1
W1	0	6
W3	5	-3

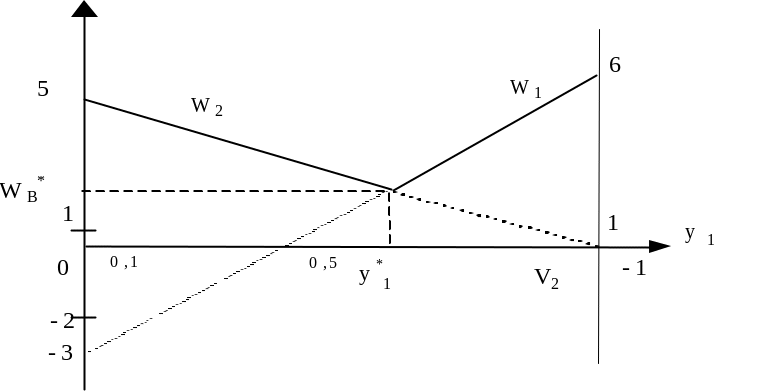
Рис. 3.2 – Графічне розв΄язання гри для гравця В

      застосовувати стратегію У результаті застосування оптимальної змішаної стратегії гравцем В його програш складає грош. один.

Аналітичий розв΄язок задачі. Оскільки стратегія для гравця В не буде використовуватись, тобто ймовірність її застосування , то платіжна матриця набуває такого вигляду, таблиця 16.

Таблиця 16

Спрощена платіжна матриця гри

	6	-3
	0	5

Для гравця А:

;

;

.

Для гравця В:

;

.

Висновок. Імовірності застосування стратегій у оптимальній змішаній стратегії гравцем А: стратегія ; стратегія .

Імовірності застосування стратегій у оптимальній змішаній стратегії гравцем В: стратегія ; стратегія ; стратегія .

Такий вибір стратегій ґарантує гравцю А виграш, а гравцю в програш у грош.од.