АААААААА

Ағымдығы сұйықтың жылдамдықтарының орналасуы мен шығыны.

Сұйық қозғалысының 2 түрі бар: ламинарлы және турбулентті. Ламинарлы дегеніміз (қатпарлы, реттелген), сұйық қатпарлары бір бірімен беттесіп қозғалады. Турбулентті дегеніміз (реттелмеген), сұйықтың бөлшектері әр уақытта өзгеріп отыратын траектория бойымен қозғалыс жасайды. турбулентті жағдайда бөлшектердің хаосты жылдамдығының әсерінен жылдамдықтарының біркелкілігі болады. Турбулентті жағдайда эпюр қисығы ламинарлыға қарағанда жалпақтау.

Сұйықтың шығындары деп ағынның көлденең қимасы арқылы өтетін («жанды» қима, яғни құбыржолының немесе арнаның толтырылған қимасы) - S уақыт бірлігіндегі оның мөлшерін атайды. Көлемді шығыны ( V, м3\с, м3\ч ) және масса шығын (М, кг\с , кг\ч) деп ажыратады.

Ауырлық күшінің әсері мен бөлшектер шөгуі

Суспензияларды седиментациялық талдау әдісін 1911 жылы А.В. Ду-

манский ұсынды. Оны әрі қарай 1912 жылы Швед ғалымы Сведберг дамытты.

Бұл әдіс тұтқыр ортада таралған бөлшектердің шөгу жылдамдығын өлшеуге

және олардың мөлшерін анықтауға негізделген. Г.С.Ходаков

″Седиментациялық әдіс үшін ең қолайлы жағдай ортаның біртектілігі және

әрбір бөлшектің қозғалуы басқа бөлшектердің қозғалуына тәуелді болмауы ″

деп жазған [3].

Суспензиялардағы бөлшектердің шөгуі ауырлық күшінің әсерінен болады.

Шар пішінді бөлшектерге әсер ететін ауырлық күшін гидростатикалық түзелт-

пелерді ескере отырып, былайша жазуға болады:

мұндағы: r – шөгетін бөлшектің радиусы;

ρ - қатты дисперстік фазаның тығыздығы;

ρо – сұйық ортаның тығыздығы;

g – еркін түсу үдеуі

Ауырлық күші әсерінен бөлшектер біркелкі-үдемелі шөгеді. Бөлшектердің шө-

гу кезінде ауырлық күшке қарама-қарсы үйкеліс күші пайда болады. Ол күш

Стокс заңы бойынша өрнектеледі: f

2 = 6π ⋅ η ⋅ r⋅ u

(2)

мұндағы: η - ортаның тұтқырлығы; u – шөгу жылдамдығы.

Шөгу жылдамдығы артқан сайын үйкеліс күші де артады, белгілі бір уақыттан

кейін ол ауырлық күшімен теңесіп, седиментациялық тепе-теңдік туады. Нәти-

жесінде бөлшектер инерциясы бойынша тұрақты жылдамдықпен шөгеді:

(3)

Бұдан, үйкеліс күші (f2) неғұрлым үлкен болса, соғұрлым ауырлық күшімен (f1)

тезірек теңесетінін және седиментациялық тепе-теңдіктің шөгу жылдамдығы-

ның (u) өте аз мөлшерінде пайда болатынын көруге болады. Жоғарыдағы (3)теңдеуден бөлшектердің шөгуінің тұрақты жылдамдығын (u) анықтауға

болады:

(4)

Бұл теңдеуден, u дисперстік фаза (ρ) мен дисперстік ортаның (ρо) тығыздықта-

рының айырмашылығына тәуелді екенін көреміз. Егер ρ > ρо болса, онда бөл-

шектер шөгеді, егер ρ < ρо болса, бөлшектер керісінше ортаның бетіне қалқып

шығады. Тұрақты жылдамдықтың u мәнімен шөгетін бөлшектердің мөлшерін r

анықтауға болады:

(4а)

Егер, тәжірибедегі барлық тұрақты шамаларды К әрпімен белгілесек:

(5)

онда тұрақты жылдамдық пен бөлшек радиусы арасындағы байланысты өрнек-

тейтін қарапайым теңдеуді алуға болады: r = K ⋅ u

2

(6), бұдан

r = K ⋅ u (7)

Тұрақты шөгу жылдамдығын u қалай анықтауға болады?

Перрен электрон зарядының шамасын өлшеу кезінде зарядталған жеке май

тамшыларының микроскопқа тамғанын байқаған. Бір ғана бөлшектің емес,

барлық бөлшектердің жылжуын бірден бақылаған ыңғайлы. Бірақ, бұл құбылыс

барлық бөлшектер бірқалыпты жылдамдықпен шөгетін және жоғарғы жағында

таза мөлдір дисперсиялық орта түзілетінін, яғни нақты шөгу шекарасы байқала-

тын монодисперсті жүйелерге тән.

Жаңа даярланған қалайы қышқылы, кальций гидроксиді, бентонитті саз жә-

не кейбір зольдер, мысалы As2S3 золдерінде шөгу осылай жүреді: As2S3 золінің

шөгуін Думанский төрт жылдан артық уақыт (1911-1916 жылдары) бақылаған.

Ол осы золь құйылған цилиндрді температурасы тұрақты, ешқандай әсер

болмайтын институттың жерастына қойған. Шекараның жылжуын өлшегенде

ол әруақытта тұрақты және 0,03 см/тәулік тең болған. Сонымен, монодисперсті

суспензиясы бар цилиндрді конвекциялық ағыны (сілкілеу, температураның өз-

геруі, т.б.) болмайтын жағдайда орналастырып, шөгетін суспензия

шекарасының белгілі бір уақытта (τ) қозғалу жолын (Н ) өлшеп, бөлшектің

шөгу жылдамдығын (u) тапқан: .

секH cмuτ= Осы мәнді (7) теңдеуге қойып,

бөлшек радиусын есептеген. Бірақ, бұл жағдайда бөлшектің шөгуі тұрақты

жылдамдықпен жүруі керек. Егер (4) теңдеуде бөлшектің мөлшері неғұрлым

үлкен болса, шөгу жылдамдығы артады да, соғұрлым ауырлық күші мен

үйкеліс күшінің арасындағы тепе-теңдік баяу орнайтыны байқалады, яғни

бөлшектің көп бөлігінің таралуы жылдамдықтың өсуіне байланысты болады.

Тәжірибе жүзінде бұл жылдамдықты өлшеу қиын. Сондықтан

седиментациялық сараптауды ауада емес, тұтқыр сұйықтықтарда және радиусы

100 Μ мен 0,1 µ аралығындағы бөлшектер үшін жүргізеді. Радиусы 100 µ үлкен

бөлшектердің шөгуі жылдам жүріп, сұйықтықта турбуленттік ағын тудырады

да, Стокс теңдеуін қолдануға мүмкін-дік тудырмайды. Радиусы 100 µ кіші

болатын бөлшектерде седиментациялық тепе-теңдіктің орнау уақытын мынамысалдардан көруге болады: суда r =50 µ болатын кварц бөлшегінің тұрақты

жылдамдықпен шөгуі τ = 3,4⋅10-3 секундта, ал r =1 µ бөлшек үшін 1,7⋅10-6

секундта қалыптасады. Егер 10 минутқа дейін шөгуді бақыласа, іс жүзінде

шөгу осындай тұрақты жылдамдықпен жүреді. Бөлшектерінің r < 0,1 µ

болатын көптеген коллоидтар үшін (Аs2S3 золінен бас-қасында) ауырлық

күшінің әсерінен шөгу байқалмайды, себебі седиментациялық тепе-теңдік

броун қозғалысының әсерінен бұзылады.

Мұндай седиментациялық талдауды жүргізу кезінде келесі жағдайларды

сақтау қажет:

1. Дисперстік фазаның бөлшектерінің тұрақты жылдамдықпен шөгуін қамта-

масыз ету керек;

2. Дисперстік орта жеткілікті мөлшерде тұтқыр болу керек. Металдың ұнтақ-

тары үшін су мен глицериннің қоспасының әртүрлі концентрациясы қол-

данылады;

3. Дисперстік фаза мен дисперстік орта арасында әрекеттесу болмау керек.

Әйтпесе, шөгу кезінде бөлшектің ісіну не солуы байқалып, оның көлемін,

тығыздығын, шөгу жылдпамдығының өзгеруі мүмкін. Дисперстік орта

индифферентті (әсерсіз) болу керек;

4. Шөгетін бөлшектер бір-бірімен әрекеттеспеу үшін, седиментацияны жүргі-

зетін цилиндр кеңірек болу керек;

5. Суспензиялардың концентрациясы жеткілікті мөлшерде сұйылған болуы ке-

рек, яғни шөгетін бөлшектер бір-біріне жанасып іріленбеуі керек, өйткені

іріленген бөлшектердің шөгу жылдамдығы өзгеше болады.

Осындай әдіспен анықталған радиус тек қана шар пішінді бөлшектерге дәл

орындалады. Басқа пішінді бөлшектер үшін бұл пәрмендік (келтірілген) радиус

деуге болады, ол есептелген шөгу жылдамдығы радиусы осындай шар тәрізді

бөлшектердікіндей деген ұғым береді.

Монодисперстік жүйелер сирек кездесетіндіктен Сведбергтің седиментаци-

ялық талдауы кеңінен қолданылмады, бірақ кейіннен ол өңделген басқа әдіс-

терде қолданылды.

Практикада бөлшектердің әртүрлі жылдамдықта шөгуін оларды мөлшеріне

және табиғатына байланысты бір-бірінен бөлуде, яғни фракциялауда қолдана-

ды, мысалы: минералды бояулар, саз, күйе, катализаторлар т.б. бір-бірінен

осылай бөлуге болады. Швед ғалымы Свен Оден полидисперстік жүйелер үшін

седиментациялық талдаудың салмақтық әдісін ашты.

Асылма қабат гидродинамикасы, сұйықтың үлбірлі ағымы мен бармотаж.

Ағындағы жылдамдықты үлкейткенде, бөлшектер арасы ұлғаяды-ағын оларды көтергендей болады. Сөйтіп бөлшектер қозғалысқа келіп, газбен және сұйықтықпен араласады. Бұл пайда болған асылды асылма қабат деп атайды. Үздіксіз қозғалыс салдарынан қатты бөлшектердің массасы оңай қозғалмалы күйге көшеді, қайнап жатқан сұйық тәріздес.

Асылма қабаттың болуы күйі мен шарттары ағын жылдамдығының өсуіне және жүйенің физикалық қасиеттеріне-тығыздығына, тұтқырлығына, мөлшеріне байланысты болады. Сұйықтың қозғалу жылдамдығына байланысты үш ағымы болады: егер V_вит>V,онда қабат қозғалмалы күйде қалады(фильтрация); егер V_вит=V, онда қабат тепе-теңдік күйінде болады(витание); егер V_вит<V, онда қатты бөлшектер ағын бағытымен қозғалады(унос).

Жалған желіну(псевдоожижение) жылдамдығы кезінде қозғалмайтын қабат күйі өзгеретін жылдамдықты айтамыз. V₀-ден V_пс-ке дейін өзгергенде қабат биіктігі мүлдем өзгермейді, ал гидравликалық кедергі артады.

Жалған желіну қабаты болуы үшін, V_пс және V_вит жылдамдықтарымен шектелген. Жұмыс жылдамдығының V₀ жалған желіну жылдамдығының бастапқысына қатынасы жалған желіну саны (число псевдоожижения) деп аталады:

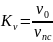
Жалған желіну жылдамдығы лабараторлық қондырғыларда және жартылайиндустриялық қондырғыларда анықталады.

Құрылыс материалдар индустриясында жалған желіну үдерісі газдар жүйесінде жиі қолданылады-қатты фаза. Бұл жүйе үшін жалған желіну аламық(неоднородный) болады: газдың жартысы қабат арқылы көпіршік түрінде немесе 1 немесе бірнеше канал арқылы өтеді.

үлкен болған жағдайда газдың көпіршік түрінде қозғалысы жалған желіну қабатының аламық болуына және биіктіктің тербелісіне әкеледі. Бұндай жағдайда көпіршіктер аппараттың мөлшеріне дейін ұлағаяды. Онда жалған желіну қабаты газды тығынмен жеке бөлшектерге бөлінеді, ал газдың олқылығы(прорыв) қатты бөлшектердің шығарылуымен жүреді. Бұндай ағым(режим) жұмысы поршдік жалған желіну деп аталады.

Жалған желіну үдерістері қазіргі таңда нақты есептеулерге тыртысады(не поддается).

Индустрияда технологиялық үдерістердің көбісі шаңмен бірге жүреді. Жұмыс істелінген газдарды шаңсыздандыру үшін ылғалды тазартуды қолданады.

Байланыс беті пайда болу үшін сұйықтық ауырлық күші салдарынан тіке немесе көлбеген қабырғамен, ал газ (немесе бу) астынан үстіге қарай бағытталады. Барботаж деп газ сұйықтық қабатымен өтіп, жеке жіңішке ағыстар, көпіршіктер, көбіктер және бүркінділерге ауысады. Сұйықтың тіке немесе көлбеген қабырғамен үлбірлі ағымы келесі жағдайларда мүмкін:

1. Үлдірдің ағыны жылжымайтын газбен байланыста

2. Үлдірдің ағыны газдың жүр-тасқынына қарсы болғанда.

Үлдірдің ағыны газдың жүр-тасқынына қарсы қозғалысының механизмі ағын жылдмадығына байланысты. Газдың аз мөлшердегі жылдамдығы сұйықтықтың ағысына ешқандай байыпты ықпалмен әсер етпейді. Жылдамдығы ұлғайғанда газдық ағын сұйықтықтың ағуын тежейді.осының салдарынан сұйықтықтың а,ын жылдамдығы азаяды, ал үлдір қалыңдығы ұлғаяды. Критикалық жылдамдық кезінде газдық ағын сұйықтық үлдірінің қабырғадан жұлқиуына немесе кері ағын үлдіріне себепші бола алады.

Құрылыс материалдар индустриясында ауамен барботаждау 2 жағдайда қолданылады:

1. Сұйық массаларды араластыру кезінде қарқындату,кейде оларды қыздырумен бірге жүреді.(соңғы жағдайда буды қолданады)

2. Эмульстялар мен көбіктерді алу үшін.

Барботаж кезінде аппараттың екі негізгі жұмысы анықталады-торсылдақты(пузырьковый) және жіңішке ағысты. Газдың аз шығындалуы кезінде торсылдақты режим байқалады. Торсылдақ ойық арқылы өткенде ең алдымен ұлғаяды,яғни Архимед күші мен кедергі күші тең болғанда:

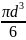g(ρ_ж – ρ_г)=πd₀σ

Барботаж - көпіршік, көбік және бүркіншіктер, бөлек ағыстардың шығуымен сұйық қабаты арқылы газдың ауысу үрдісі

Агрегатты жагдаяттың күйіндегі жылу алмасу. Агрегатты күй өзгергендегі жылу алмасу кезінде (қыздырғанда, суытқанда) материал агрегаттық жағдайын өзгертеді: бу шығару, конденсация, балқу, кристалдану. Сонда жылу берілісте критериалды теңдіктер қосымша агрегатты жағдаяттың өзгеру жылуын есепке алады. Құрылыс материалдарының технологиялық процестері үшін әр түрлі жағдайда жылу алмасуда агрегатты күйдің өзгеруі мағына бере отырып, будың конденсациясы кезінде жылу алмасу, еру мен жүзу кезінде жылу алмасу жіне сұйықтың қайнау кезіндегі сирек жылу алмасу.

БББББББББ

Бейньютондық сұйықтық.

Бейньютондық сұйықтықтың тұтқырлығы тұрақсыз,ол жылжу жылдамдығына тікелей байланысты. Құрылыс материалдар технологиясында бұндай сұйықтықтарға цементтік шлам мен ашпаларды(растворы), бетондық қоспаларды, полимерлер ашпасын және т.б жатқызамыз. Межелу кернеуінің жылдамдық градиентіне қатысты графигі ағыстың қисығы деп аталады.

Қазіргі қағида бойынша бейньютондық сұйықтықтыр 3 топқа жіктеледі.

Бірінші топқа тұтқырлы немесе стационарлық бейньютондық сұйықтықтар жатады(олар үшін бұл функция τ=ϯ(dv/dy) уақытқа тәуелсіз).

Екінші топқа бингамдық қисықтағы псевдоилемді және дилитантты сұйықтықтар кіреді. Бингамды сұйықтықтар қозғалысы тек қана τ₀≥τ жағдайда,яғни жүйедегі құрылымды бұзу үшін орындаланда болады. Бұндай қозғалысты иілмді деп атаймыз. Ал τ_0-ағу шегі деп атаймыз.

Бингам денесінің құрылымы межелу кернеуі салдарынан бірден бұзылады, бұл өз алдына бингам денесінің сұйық күйіне айналдырады. Егер межелу кернеуін алып тастаса, дене бастапқы қатты күйіне оралады. Шведов – Бингам теңдеуделері:

Ребиндер мен Михайлов ағудың ең төменгі шегін, оның нағыз ағу шегі деп атайды.

Псевдоиілімді сұйықтықтыр -ның ең кішкентай мөлшерінен бастап ағады. Ол тұтқырлық мәнінің қисықтағы әрбір нүктеде градиен жылдамдығына байланысты болады.

Оствальд ережесі бойынша:

K және m тұрақты коэффиценттер, m<1.

К коэффиценті сұйықтықтың консистенциясына байланысты, тұтқырлық өсуімен ұлғаяды.

Псевдоиілімді сұйықтықтарға полимерлер ашпасы(раствор), целлюлозалар, суспензиялар жатады.

Делитантты сұйықтықтарға крахмал суспензиясы, Т/Ж қатынасы үлкен болатын әртүрлі клейлер жатады. Псевдоиілімді сұйықтықтарға қарағанда бұл сұйықтықтардың тұтқырлығы жылдамдық градиентінің өсуімен ұлғаяды. Олардың ағыны да Оствальд теңдеуімен m>1 кезінде өрнектеледі.

Жылжудың ұзақтығының құрылымға әсері салдарынан сұйықтықтар тиксотропты және реопектантты болып бөлінеді. Тиксотропты сұйықтықтарда межелу кернеуі өсуімен құрылымы бұзылады, ал ағымдылығы ұлғаяды. Кернеуді алып тастағанннан кейін сұйықтықтың құрылымы бірте-бірте қалпына келеді. Тиксотропты сұйықтықтарға мысал ретінде көптеген бояғыштарды жатқызуға болады. Реопектантты сұйықтықтарда межелу кернеуі өсуімен ағымдылығы төмендейді. Оларға коллоидты ашпалар мен бентонитті балшықтардың суспензиялары жатады.

Үшінші топқа тұтқырлы-иілімді және максвельдік сұйықтықтар жатады. Бұл сұйықтықтар кернеуі бар кезінде қозғалады, ал кернеуді алып тастаса өзінің алғашқы пішінін бірте-бірте қалпына келтіреді.

Бингамдық сұйықтықтар үшін ламинарлық қозғалыс кезіндегі шығын теңдеуі Бэкингам теңдеуі деп аталады, ол келесі түрде болады:

Оствальд заңына бағынатын сұйықтықтар үшін, ламинарлы қозғалыс кезіндегі шығын келесі формула арқылы табылады:

Бұйымдарды қалыптандырудың әдістерін жіктеу және жалпы заңдылықтары. Бұйымдарды қалыптандыру үрдісінің негізгі тағайындалуы-жартылай фабрикатты керек формада алу.Бірақ бұл жалғыз мақсат емес жартылай фабрикатты керекті тығыздықта және ақаусыз ішкі структурасын алу.Құрылыс бұйымдары келесі әдістермен дайындалады:виброландыру,центрифугирлеу,престеу(құрғақ,жартылай құрғақ),пластикалық қалыптау және құю және вакумдау.Қалыптаудың түрін қалыпталынатын массаның қасиеттеріне және өнім түріне байланысты таңдайды.Массаның қалыпталуының қасиеттерін илемділік пен консистенция ұғымдары айқындайды.Илемділік-массаның кайтымсыз деформацияларға біркелкілігін жоғалтпай шыдау қабілеті:=/, мұндағы -илемділік көрсеткіші;- беріктік шегі,-илемді тұтқырлық.

ГГГГГГГ

Гидромеханикалық үрдістер мен аппараттардың жалпы ұғымдары

Гидромеханика-сұйықтар мен газдардың жылдамдықтарын қарастыратын ғылым. Гидромеханика заңдары, тыныштық қалпы мен тепе-теңдік жағдайын қарастыратын - гидростатика мен сұйықтың жылдамдықтарының заңдарын қарастыратын-гидродинамикадан тұратын гидравлика бөлімінде қарастырады. Гидромеханикалық үрдістердің классификациясын басқа классификациялық белгілерге бағындыруға болады: ағындар қозғалысының салдарын қарайтын заңдар. Теориялық гидродинамика гидромеханикалық үрдістің 2 бөлімін қарастырады.: гидродинамиканың ішкі есептерін қарастыратын үрдістер (мыс, арынның труба бойымен қозғалысы); сыртқы есептерін шешетін үрдістер (мыс, ауырлық күшінің әсерінен шөгетін бөлшектер қозғалысы). Гидравликаның негізгі заңдарын қорытындылағанда идеалды сұйық түсінігін енгізеді. Ол тұтқыр сұйыққа қарағанда сығылмайды, температура өзгерген сайын тығыздығы өзгермейді

Гидростатика. Эйлер тепе-теңдігінің дифференциалдық теңдігі мен гидростатиканың негізгі теңдігі

Гидростатика – гидромеханиканың сұйықтықтардың тепе-теңдігін және қимылсыз тұрған сұйыққа батырылған дененің әсер етуін зерттейтін бір бөлімі. Гидростатиканың бұл теңдеуін шешкен кезде — М.Эйлер теңдеуі пайдаланылады Статиканың негізгі қағидасы бойынша, тепе-теңдікте тұрған, берілген көлеміне әсер ететін күштер проекциясы нольге тең. Эйлер тепе теңдігінің дифф.теңдігі

гидростатиканың негізгі теңдігі:

сұйықтың ірбір нүктесінде биіктік пен статикалық арын тұрақты.

Гидростатиканың негізгі теңдігі және оны іс жүзінде қолдану.

Гидростатика теңдеуі — сығылмайтын сұйықтықтың гидростатикалық қысымын анықтайтын теңдеу, яғни:

, мұндағы — бастапқы гидростатикалық қысым деп аталатын сұйықтықтың бос бетіне түсірілетін қысым; — сұйықтықтың тығыздығы; гидростатикалық қысымы анықталатын нүктенің орналасу терендігі; — қимасының ауданы бір өлшем, биіктігі сұйық бағананың салмағына тең артық қысымъ

Гидростатиканың негізгі теңдеуі — сығылмайтын сұйықтықтың гидростатикалық қысымын ( ) анықтайтын теңдеу, яғни:

λ , мұндағы — сұйықтықтың еркін бетінің астында берілген нүктенің батырылу шамасы ретінде қарастырылады. Демек, гидростатиканың негізгі теңдеуі сұйықтықтың толық гидростатикалық қысымы үлестірім заңдылығының математикалық өрнегі болып табылады. Сұйықтықтың еркін бетіне қатысты тереңдікте орналасқан белгілі кез келген нүктедегі толық гидростатикалық қысымның шамасы. Сұйықтықтың еркін бетіне түсірілген сыртқы қысым мен биіктігі қарастырылып отырған нүктенің орналасу терендігіне ( ) тең және негізінің ауданы бірге тең сұйық бағаны салмағының қысым қосындысына тең. Гидростатиканың негізгі теңдеуі сұйықтықтың бетіне түсірілетін сыртқы қысым сұйық көлемінің барлық жақтарына бірдей қарқындылықпен таралатынын көрсетеді. Мұны Паскаль заңы да растайды