Гаусс теоремасы

Кез келген ауданнан өтетін векторының ағыны :

(6.8)

болады. Осыған байланысты атап өтетін бір жай: аудан тұйық болған кезде, оған түсірілген нормальдың оң бағыты ретінде сыртқы нормаль алынады: яғни нормальдың бәрі ауданнан сыртқа қарай бағытталады.

:

болады.Электр өрісін …, нүктелік заряд тудыратын болса, онда суперпозиция принципі бойынша қорытқы ағын:

Егер зарядтар тұйық беттің ішіне орналасқан болса, онда теңдіктің оң жағындағы әр интеграл -ге тең болар еді. Сондықтан:

(6.9)

деп жазуға болады. Бұл (6.9) теңдеу Гаусс теоремасының математикалық өрнегi.

1. Электрстатикалық өрісте заряд орын ауыстырғанда орындалатын жұмыс. Нүктелік зарядының өрісінде екінші нүктелік заряд 1-ші нүктеден 2-ші нүктеге қайсыбір траекториямен қозғалсын.

зарядын 1-ші нүктеден 2-ші нүктеге дейін орын ауыстырғанда орындалатын жұмыс:

, (6.10)

мұндағы мен - зарядынан қозғалушы орналасқан бастапқы және соңғы нүктелерге дейінгі қашықтықтар. Егер бірнеше нүктелік зарядтардың өрісінде қозғалатын болса, оған суперпозиция принципі бойынша, күші әсер еткендіктен, атқарылатын жұмыс әр күш жұмыстарының алгебралық қосындысына тең, яғни

, (6.11)

бұл жердегі мен мөлшері зарядтан орналасқан бастапқы және соңғы нүктелерге дейінгі қашықтық. Егер қозғалушы зарядты бірлік өлшемді зарядқа тең деп алсақ, онда (6.11) теңдіктен:

,

немесе . (6.12)

Бұл интеграл электрстатикалық өрістің кернеулік векторының тұйық контур бойымен циркуляциясы деп аталады.

Электрстатикалық өріс потенциалы. Потенциалдық өрістегі консервативтік күштер жұмысы потенциалдық энергияның кемуі нәтижесінде орындалады:

. (6.13)

Демек, зарядының заряды өрісіндегі потенциалдық энергиясы:

. (6.14)

Өрістің потенциалы:

. (6.15)

Кернеулік векторы мен потенциал арасындағы байланыc:

немесе , (6.16)

мұндағы - Набла операторы. (11.16) бойынша - кернеулік теріс таңбамен алынған потенциалдың градиентіне тең болады.

Оқшауланған өткізгіштің электрлік сыйымдылығы

Заряд пен потенциал арасында q=Cj тәуелділігі бар екені тәжірибеден белгілі:

. (6.17)

Конденсатор сыйымдылығы:

, (6.18)

Бұдан жазық конденсатордың сыйымдылығы:

, (6.19)

мұндағы – астарлар арақашықтығы; – астарлар арасын толтыратын ортаның диэлектрлік өтімділігі. Цилиндрлік конденсатордың сыйымдылығы:

, (6.20)

мұндағыl – конденсатордың ұзындығы; мен – ішкі және сыртқы цилиндрлік астарлардың радиустары. Сфералық конденсатордың сыйымдылығы:

, (6.21)

мұндағы мен – ішкі және сыртқы астарлардың радиустары.

Диэлектриктердің поляризациясы. Поляризациялану.

Поляризациялану – диэлектрикте сыртқы зарядтар туғызған өріс кернеулігінің кемуіне әкеледі. Егер вакуумда зарядтардың өзара әсерлесу күші , ал диэлектриктегі күші болса, онда Кулон заңына сәйкес

болатындықтан, диэлектрикті ортадағы кернеулікті деп жаза аламыз. Диэлектриктердің поляризациялану дәрежесін сипаттау үшін көлем бірлігіндегі дипольдік моментті анықтау керек, ол үшін шексіз аз көлемді бөліп алып, осы көлемдегі молекулалардың моменттерінің қосындысын сол көлемге бөлу керек:

(6.22)

Кезкелген изотропты диэлектрик түрлері үшін берілген нүктедегі поляризациялану векторы, өрістің кернеулігімен байланысы мынадай болады:

= æ·₀ , (6.23)

мұндағы æ – диэлектрлік қабылдағыштық деп аталады, ол шамасына тәуелсіз.

Диэлектриктің ішіндегі өрістің толық кернеулігі

= + (6.24)

болады. Диэлектриктен тыс жерде поляризация болмайды =0, сондықтан = .Электрстатикалық индукцияның анықтамасыбойынша = :

= + . (6.25)

Бұл формуладағы мәнін(6.25) қойсақ төмендегідей өрнек аламыз:

= ( +æ )= (1+ æ) . (6.26)

Өзін-өзі бақылауға арналған тесттер:

1. Зарядталған шар ішіндегі өріс потенциалы оның центріне дейінгі арақашықтыққа мына түрде байланысты: φ = аr² + b. Мұндағы а мен b тұрақты шамалар. Шар ішіндегі көлемдік зарядтың бөлінуін ρ(r) табу керек.

A)

B)

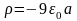
C)

D)

E)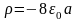

2. Тұрақты σ беттік тығыздықпен зарядталған, радиусы R сфераның центіріндегі потенциалды табу керек.

A) =R/

B) = R/

C) =R/

D) =2R/

E) =R/

3. Диаметрі d = 2 см метал шарик φ = 150 B потен-циалға дейін теріс зарядталған. Шарик бетіндегі n электрондар санын табу керек.

A)𝑛 = 1,04 10 ⁵

B)𝑛 = 1,04 10 ⁸

C)𝑛 = 2,24 10 ⁹

D) 𝑛 = 1,04 10 ⁹

E)𝑛 = 1,84 10 ⁹

4. Радиусы R шар ρ көлемдік тығыздықпен біркелкі зарядтталған. Шардың ішіндегі нүктелердің φ потенциалын шардың центріне дейінгі арақашықтықтың функция ретінде табу керек.

A) ( 1- )

B) ( 1- )

C) ( 2- )

D) ( 1- )

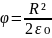E) ( 1- )

5. q₁ = 3,7·10^-5 Кл және q₂ = 6,2·10^-5 Кл оң зарядтар вакуумда бір-бірінен r₁ = 2,7 м арақашықтықта орналасқан. Зарядтарды r₂ = 45 см арақашықтыққа дейін жақындату үшін қандай А жұмыс атқару қажет?

A)А=2q₁q₂ / (4 π ε₀) (1/r₂ – 1/r₁)

B)А=q₁q₂ / (4 π ε₀) (1 – 1/r₁)

C)А=q₁q₂ / (π ε₀) (1/r₂ – 1/r₁)

D)А=q₁q₂ / (4 π ε₀) (1/r₂ – 2/r₁)

E)А=q₁q₂ / (4 π ε₀) (1/r₂ – 1/r₁)

7-дәріс

Тұрақты электр тогы. Ом және Джоуль-Ленц заңдары. Кирхгоф ережелері.

Электр тогының жүру шарттары. Металдардың электрлік өткізгіштігі.

Бөгде күштер. Гальваникалық элементтің э.қ.к.

Шалаөткізгіштердің электр өткізгіштігі. Электролиз.

Электр зарядтарының бір бағыттағы реттелгенқозғалысын электр тогы деп атайды. Ток күші деп бірлік уақытта өткізгіштің көлденең қимасынан өтетін заряд мөлшерімен өлшенетін скаляр шаманы айтады. Егер dt уақытта мөлшері dq заряд тасымалданса, онда ток күші

. (7.1)

болады. Ток тығыздығы векторы ток бағытымен бағытталған және оның сан мәні ток бағытына перпендикуляр dS ауданы арқылы өтетін dІ ток күшінің осы ауданға қатынасына тең болады:

, (7.2)

мұндағы - тогы өтетін аудан. Ток тығыздығы үшін Ом заңы:

. (7.3)

Бұл өрнектердегі - меншікті электр өткізгіштігі, оған кері шама, яғни - өткізгіштің меншікті кедергісі деп аталады.