Тұтас орта механикасының элементтері

Гидродинамика – сұйық орта қозғалыстарының заңдылықтарын және оның денелермен әрекеттесуін зерттейтін механиканың бір саласы.

Сұйық сығылмайды деп есептесек, онда бұл көлемдер бір-біріне тең:

(3.1)

Осы өрнекті ағынның үздіксіздік теңдеуі деп атайды. Ағын түтігі көлденең қимасының сұйық ағысының жылдамдығына көбейтіндісі тұрақты шама.

Бернулли теңдеуі

, (3.2)

Қималарды ток түтікшесінің кез-келген нүктесінен алуға болатындықтан соңғы теңдеуді мына түрде жазуға болады:

(3.3)

Ағын түтігі горизонталь орналасса Бернулли теңдеуі ( ):

(3.4)

Сұйықтық горизонталь аққан кезде үйкеліс болмаса динамикалық және статикалық қысымының қосындысы ток түтікшесі қимасының барлық нүктелерінде бірдей болады.

, (3.5)

Және ағын жылдамдығын алуға болады.

. (3.6)

Онда тесіктен аққан сұйықтықтың жылдамдығын Торричелли өрнегі деп атайды:

_. (3.7)

Тұтқырлық

Тұтқырлық депнақты сұйықтықтардың қабаттар арасында ішкі үйкеліс құбылысының пайда болуы айтылады. Ньютонның зерттеулері бойынша бұл күштің шамасы мынадай өрнекпен анықталады:

, (3.8)

мұндағы –жылдамдық градиенті, ол осьі бағытында бір қабаттан екіншісіне өткен кезде жылдамдық қалай тез өзгеретінін көрсетеді; – жанасатын қабаттардыңбетінің ауданы; – динамикалықтұтқырлық коэффициенті. Ішкі үйкеліс күшінің шамасы қабаттарының беттесу ауданына және жылдамдықтың градиентіне пропорционал.

Сұйықтық ағынының екі түрі

Сұйықтықтың ағысы ламинарлық және турбуленттік деп екіге бөлінеді. Сұйықтықтың жеке қабаттары бір-біріне қарағанда параллель, яғни сұйық қабатта бірі-бірімен араласпай қозғалатын болса, онда ол ағыс ламинарлық деп аталады.

Түтік бойымен сұйық ағысы кезіндегі ағыстың бір түрінен екінші түрге көшу шарты Рейнольдс саны деп аталатын шамамен анықталады.

, (3.9)

мұндағы: –кинематикалық тұтқырлық, –сұйықтықтың тығыздығы, – орташа ағыс жылдамдығы, – түтік диаметрі. Егер ішкі үйкеліс күші және ағыс жылдамдығы аз болса, онда қозғалысты ламинарлық деп қарастыруға болады. Турбуленттік ағысқа өту үшін Рейнольдс саны мына аралықта болуы керек . кезінде ағыс ламинарлық болады. Тұтқырлықтың әсерінен кезінде түтіктің дөңгелек қимасының әртүрлі қабаттардағы ағыс жылдамдықтары әртүрлі болады. Оның орташа мәні Пуазейль өрнегі бойынша анықталады.

, (3.10)

мұндағы -түтік радиусы, ( ) –түтік ұштарындағы қысым айырымы, -оның ұзындығы .

Мысалы, Стокс сұйықтықта қозғалған радиусы r, жылдамдығы шарға әсер ететін күші үшін келесі өрнекті анықтады:

, (3.11)

r – шар радиусы, - оның қозғалыс жылдамдығы. Бұл өрнек Стокс теңдеуі деп аталады.

Арнайы салыстырмалы теорияның элементтері

Арнайы салыстырмалылықтың теорияныңнегізін Эйнштейн тұжырымдаған екі постулат құрайды.

1. Табиғаттың барлық заңдары бір инерциалды санақ жүйесінен екінші инерциалды санақ жүйесіне өтуіне қатысты өзгермейді (инвариант болады).

2. Жарықтың вакуумдағы жылдамдығы барлық инерциалды санақ жүйелерінде бірдей және жарық көзі мен қабылдағыштың қозғалу жылдамдығына тәуелсіз.

Бұл постулаттардан төмендегі өте маңызды салдарлар келіп шығады:

1. Ұзындықтың қысқаруы

,

2. Массаның артуы

,

3. Уақыттың баяулауы

,

4. Жылдамдықтарды қосу ережесі

,

5) Дененің толық энергиясы

.

Лоренц түрлендірулері мына түрде анықталған:

, , , . (3.12)

Релятивистік динамика элементтері

Импульстің жылдамдыққа тәуелділігі классикалық механикаға қарағанда біршама күрделі екендігі көрінеді.

. (3.13)

Өзін-өзі бақылауға арналған тесттер:

1.Массасы импульсі p₁ болатын 1 бөлшек тыныш тұрған массасы 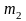болатын 2 бөлшекпен серпімді соқтығысады. Бөлшектердің соқтығысудан кейінгі p¹₁ және p¹₂ импульстарын табу керек. Соқтығысудың нәтижесінде 2 бөлшек 1 бөлшектің бастапқы бағытымен бұрышпен ауытқиды.

A) ;

B) ;

C) ; .

D) ;

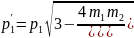E) ;

2. Идеал сұйық көлбеу жазықтықпен стационар ағады. Ағын тереңдігі l арақашықтықта екі есе кемиді. Қандай арқашықтықта ағын тереңдігі төрт есе кемиді?

A) 2l

B) 4l

C) 3l

D) 6l

E)5l.

3. Биік цилиндр ыдыстың түбіндегi саңылаудан су ағады. Ыдыс қимасының ауданы саңылау қимасының ауданынан 100 есе үлкен. Ыдыстағы судың деңгейі араласатын үдеуді табу керек.

A) 10^-3g

B)9g.

C) .

D) 10^-8g

E)10g

4. Радиусы R = 0,2 м біртекті дискінің жиегіне F = 98,1 H тұрақты жанама күш түсірілген. Айналу кезінде дискіге Мүйк = 4,9 Н∙ м үйкеліс күшінің моменті әсер етеді. Диск тұрақты 100 рад/с бұрыштық үдеумен айналады. Дискінің массасын анықтау керек.

A)

B)

C)

D)

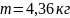
E)

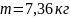
5. Қандай жылдамдықта бөлшектің кинетикалық энергиясы оның тыныштық энергиясына тең болады?

A) 1,3 м/с

B) м/с.

C) 4,3 м/с

D) 9,3 м/с

Е)1,6 м/с

4-дәріс

Термодинамикалық параметрлер және процестер. Идеал газ күйінің теңдеуі.

Идеал газдың молекула-кинетикалық теориясы. Статистикалық таралу.

Тасымалдау құбылыстары. Диффузия. Тұтқырлық. Жылу өткізгіштік.

Термодинамикалық параметрлер мен процестер

Жүйенің күйін сипаттау үшін жүйенің термодинамикалық параметрлері (күй параметрлері) деп аталатын физикалық шамалар енгізілген. Оларға р– қысым, – көлем, Т – температура, п – концентрация және т.б. жатады.

Қысым р– дененің бірлік бетіне нормаль бойымен әсер ететін күшке тең шама Өлшем бірлігі – Па (Паскаль) ( ).

Жүйенің температурасы– оның бөлшектерінің жылулық қозғалыс қарқынының өлшемі. Физикада бірнеше температуралық шкала қолданылады. Мысалы, Кельвин ( ) және Цельсий ( ) шкалаларындағы температуралар өзара

T = t + 273,15 (4.1)

өрнегімен байланысқан.

Қалыпты күйдетермодинамикалық параметрлер келесі мәндерге тең болады:

p=1,013· 10⁵ Па, V_M=22,4· 10^-3 м³ , T=273,15K . (4.2)

Термодинамикалық процесс деп жүйенің кез-келген параметрінің өзгерісін айтады.

Идеал газдың күй теңдеуі

Идеал газдың күй теңдеуі– термодинамикалық параметрлер арасындағы функционалдық байланыс: :

. (4.3)

Мұндағы V– газдың молярлық көлемі; – универсал газ тұрақтысы . Бұл Менделеев – Клапейронтеңдеуі. Бұл теңдеуді тағы бір түрде жазуға болады: немесе

. (4.4)

Мұндағы: – мөлшері 1 моль заттағы молекулалар санына тең Авогадро саны, – Больцман тұрақтысы, – молекулалар концентрациясы (бірлік көлемдегі газ бөлшектерінің саны). Тұрақты температурада газ қысымы молекулалардың концентрациясына пропорционал болады.

Идеал газ үшін молекула-кинетикалық теорияның негізгі теңдеуі

, (4.5)

мұндағы –молекула массы, п –молекулалар концентрациясы; – газ молекулаларының ілгерілемелі қозғалысының орташа квадраттық жылдамдығы (көп жағдайда түрінде белгіленеді).

Газ молекулаларының ілгерілемелі қозғалысыныңорташа кинетикалық энергиясы:

. (4.6)

Жоғарыдағы (4.4) және (4.5) өрнектерінен келесі келесі өрнекті шығаруға болады:

. (4.7)

Бұдан идеал газдың бір молекуласының орташа кинетикалық энергиясы тек Т термодинамикалық температураға ғана тәуелді екенін көреміз:

. (4.8)

Соңғы өрнек идеал газ молекуласының термодинамикалық орташа кинетикалық энергиясы ( К) температураға пропорционал болатынын көрсетеді.

Энергияның еркіндік дәрежелер бойынша бірқалыпты таралу заңы

Дененің еркіндік дәрежесі (і) деп оның кеңістіктегі орнын толық анықтауға қажет тәуелсіз координаталардың ең аз санын айтады.

Идеал газдың қатаң байланысқан молекулалары үшін і мәні 4.1-кестеде берілген.

4.1–кесте

Еркіндік дәрежесінің саны	Біратомды газ	Екіатомды газ	Көпатомды газ
Ілгерілемелі	3	3	3
Айналмалы	0	2	3
Барлығы	3	5	6

Кестеден молекула үшін ілгерілемелі қозғалыстың еркіндік дәрежесі әрқашан үшке тең болатынын көреміз. Ілгерілемелі қозғалыстың әр еркіндік дәрежесіне бір атомды молекуланың орташа кинетикалық энергиясының үштен біріне (1/3) сәйкес келеді:

. (4.9)

Сондықтан, молекуланың еркіндік дәрежесі і болса, онда оның орташа кинетикалық энергиясы мына шамаға тең болады:

. (4.10)

Мөлшері 1 моль және массасы т кез-келген газдың ішкі энергиясы келесі өрнектермен анықталады:

және (4.11)

Сыртқы күш өрісіндегі бөлшектер үшін Больцман таралуы

Біртекті ауырлық күші өрісіндегі идеал газ қысымының биіктікке байланысты өзгеруі барометрлік формуламен анықталады:

, (4.12)

мұндағы:р мен р₀ – газдың h және h = 0 биіктіктердегі қысымы, – газдың мольдік массасы. Осы өрнек пенкүй теңдеуі бойынша Больцман таралуы деп аталатын концентрацияның сыртқы потенциалдық өрісте биіктікке байланысты өзгеру заңын алуға болады:

немесе , (4.13)

мұндағып мен п₀ – газдың h және h = 0 биіктіктердегі концентрациясы, т₀ – молекула массасы, - бөлшектің потенциалдық энергиясы.

Барометрлік өрнек бойынша қысым арқылы (4.13) биіктікті анықтауға болады:

. (4.14)

Газ молекулаларының жылдамдықтар бойынша таралу заңы (Максвелл заңы)

Ықтималдылық теориясын қолдана отырып, 1860 жылы Максвелл идеал газ молекулаларының жылдамдықтар бойынша таралу заңын анықтады:

(4.15)

мұндағы - таралу функциясы.

Функцияның нақты түрі газ тегіне (молекула массасы ) және оның температурасына байланысты. Қысым мен көлем молекулалардың жылдамдықтар бойынша таралуына әсер етпейді. Таралу функциясы максимум болатын жылдамдық ең ықтимал жылдамдық деп аталады.

4.2 –сурет. Максвелл таралуы

4 .1– сурет. Таралу функциясының экстремумдары

Таралу заңынан газдың берілген күйін сипаттайтын жылдамдықтарды анықтауға болады (7.2 – сурет; 7.2 – кесте).

4.2 – кесте

Ең ықтимал жылдамдық	Орташа арифметикалық жылдамдық	Орташа квадраттық жылдамдық