1.6. Второй закон термодинамики
Второй закон термодинамики определяет направление, в котором протекают процессы, устанавливает условия преобразования тепловой энергии в механическую, а также определяет максимальное значение работы, которая может быть произведена тепловым двигателем.
Второй закон термодинамики математически может быть выражен следующим образом:
(1.117)
Таблица. 1.5
Характеристики основных термодинамических процессов идеального газа
Характеристика процесса |
Название процесса |
||
Изохорный |
Изобарный |
Изотермический |
|
Показатель политропы |
∞ |
0 |
1 |
Уравнение процесса |
V=const; P/T=const |
P=const; V/T=const |
T=const; PV=const |
Теплоемкость. кДж/(кг·К) |
Cv |
Сp= Cv+R |
∞ |
Изменение внутренней энергии ∆u1-2=u2-u1 (кДж/кг) |
Сv(Т2-Т1) |
Сv(Т2-Т1) |
0 |
Изменение энтальпии ∆h1-2=h2-h1 (кДж/кг) |
Cp(Т2-Т1) |
Сp(Т2-Т1) |
0 |
Изменение энтропии ∆s1-2=s2-s1 (кДж/кг) |
Cvln Т2/Т1 |
Сpln Т2/Т1 |
|
Количество теплоты q1-2 (кДж/кг) |
Cv(Т2-Т1) |
Сp(Т2-Т1) |
|
Работа изменения объема l1-2 (кДж/кг) |
0 |
P(V2-V1)=R(T2-T1) |
|
Работа техническая l’1-2 (кДж/кг) |
-V(Р2-Р1)=v( P1- P2)= =R(T1-T2) |
0 |
l’1-2=
l1-2=
q1-2=
= |
Продолжение табл. 1.3.
Характеристика процесса |
Наименование процесса |
|
Адиабатный |
Политропный |
|
Показатель политропы |
k= Сp/Сv |
|
Уравнение процесса |
РVk=const |
РVn=const |
Теплоемкость. кДж/(кг·К) |
0 |
|
Изменение внутренней энергии ∆u1-2=u2-u1 (кДж/кг) |
Сv(Т2-Т1) |
Сυ(Т2-Т1) |
Изменение энтальпии ∆h1-2=h2-h1 (кДж/кг) |
Сp(Т2-Т1) |
Сp(Т2-Т1) |
Изменение энтропии ∆s1-2=s2-s1 (кДж/кг) |
0 |
|
Количество теплоты q1-2 (кДж/кг) |
0 |
|
Работа изменения объема l1-2 (кДж/кг) |
|
|
Работа техническая l’1-2 (кДж/кг) |
|
|
где dS – бесконечно малое приращение энтропии системы; dQ – бесконечно малое количество тепла, полученного системой от источника тепла; T – абсолютная температура источника тепла.
Знак неравенства соответствует необратимым процессам, а знак равенства – обратимым процессам. Следовательно, аналитическое выражение второго закона термодинамики для бесконечно малого обратимого процесса имеет вид:
(1.118)
а так как согласно первому закону термодинамики:
то уравнение (1.118) принимает следующий вид:
ЭНТРОПИЯ ИДЕАЛЬНОГО ГАЗА
Основным уравнением для определения изменения энтропии в обратном процессе является выражение:
(1.119)
Поскольку в технической термодинамике приходится иметь дело не с абсолютным значением энтропии, а с ее изменением, отсчет значений энтропии можно вести от любого состояния. Для газов принято считать значение энтропии равным нулю при нормальных условиях, т. е. при t = 0o C и P = 760 мм. рт. ст.
Определение энтропии для любого состояния газа при постоянной теплоемкости, отсчитанной от нормального состояния, производят по следующим формулам:
(1.120)
(1.121)
(1.122)
Изменение энтропии между двумя произвольными состояниями газа 1 и 2 при постоянной теплоемкости определяют по следующим формулам:
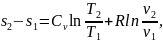(1.123)
(1.124)
(1.125)
Уравнения кривых различных термодинамических процессов в системе координат Ts имеют следующий вид (при постоянной теплоемкости):
уравнение изохоры:
(1.126)
уравнение изобары:
(1.127)
Взаимное расположение изохоры и изобары показано на рис. 1.7.
Рис. 1.7. Взаимное расположение изохоры и адиабаты в координатных
осях TS
уравнение изотермы:
T = const.
При этом изменение энтропии в изотермическом процессе равно:
(1.128)
Уравнение адиабаты:
s = const. (1.129)
Изображение изотермы и адиабаты в системе координат TS и Pυ дано соответственно на рис. 1.8 и 1.9.
Рис. 1.8. Изображение изотермы в координатных осях TS
Рис. 1.9. Изображение адаибаты в координатных осях Pυ
Уравнение политропы:
(1.130)
где:
Широким распространением при решении термодинамических задач пользуется диаграмма TS. Адиабаты в этой диаграмме изображаются вертикалями, изотермы – горизонталями, изохоры и изобары идеального газа – логарифмическими кривыми.