2.3. Процессы истечения и дросселирования газов и паров

При решении задач связанных с истечением газа (рис 2.2.) через насадки (сопла) чаще всего приходится определять скорость истечения и расход, т.е. количество газа в единицу времени.

Рис. 2.2. Истечение газа через сопло

Рассмотрение закономерностей движения газов и паров по каналам имеет чрезвычайно большое значение для изучения рабочих процессов ряда машин, аппаратов и устройств (паровые и газовые турбины, эжекторы, реактивные и ракетные двигатели, горелочные устройства и т. п.).

Процессы истечения обычно начинают изучать, принимая следующие допущения:

а) с течением времени условия движения газа и его параметры не изменяются – стационарная задача;

б) отсутствует теплообмен между потоком газа и внешней средой –адиабатная задача;

в) во всех точках данного поперечного сечения канала скорость и физические параметры газа одинаковы и изменяются только по длине канала – одномерная задача.

При указанных допущениях движение газа (пара) удовлетворяет условиям установившегося движения:

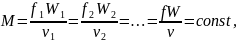(2.21)

где М – массовый секундный расход газа, кг/с; – площади поперечных сечений канала, м²; - удельные объемы газа в соответствующих сечениях канала, м³/кг; - скорости истечения в соответствующих сечениях, м/с; P₁, P₂-давление среды на входе и на выходе в сопло соответственно, Па.

В процессах изменения состояния движущегося с конечной скоростью газа теплота расходуется не только на изменение внутренней энергии и на совершение внешней работы (против внешних сил), но и на приращение внешней кинетической энергии газа при его перемещении по каналу. Применительно к потоку газа, движущегося со скоростью W, выражение первого закона термодинамики имеет вид (в дифференциальной форме):

(2.22)

где dq – теплота, подводимая к потоку; du – изменение внутренней энергии рабочего тела; dl_n – работа по преодолению внешних сил сопротивления (работа «проталкивания»); d(W²/2) – изменение кинетической энергии 1 кг рабочего тела, движущегося со скоростью W.

Работа проталкивания на единицу массы равна:

=d(pυ). (2.23)

С учетом (2.23) выражение (2.22) можно записать как:

, (2.24)

или:

.

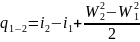Уравнение (2.24) показывает, что подведенная теплота в процессе при течении газа (или жидкости) расходуется на изменение внутренней энергии, на работу проталкивания и на изменение внешней кинетической энергии рабочего тела или подведенная теплота при течении газа расходуется на изменение его энтальпии и внешней кинетической энергии.

В случае адиабатного истечения через сопло (рис. 2.3) легко найти скорость истечения на выходе (сечение 2), используя выражение (2.24).

Рис. 2.3. Адиабатное истечение через сопло

Скоростью W₁ на входе в сопло обычно пренебрегают:

(2.25)

В формуле (2.25) энтальпия выражена в Дж/кг. Если же она выражена в кДж/кг или в ккал/кг, то формула (2.25) соответственно примет вид (2.26) или (2.27); скорость во всех случаях получается в м/с:

(2.26)

(2.27)

Значения энтальпии определяются по is -диаграмме или по таблицам для данного вещества.

В тех случаях, когда не известна энтальпия рабочего тела, удобнее определять скорость через основные параметры P, υ, T. Формулу для определения скорости адиабатного истечения идеального газа легко получить, используя таблицу 2.1 и пренебрегая величиной W₁.

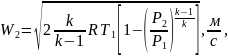(2.28)

или:

(2.29)

где k и R – соответственно показатель адиабаты и газовая постоянная рабочего тела.

Массовый расход газа определяется из выражения (2.21), которое после подстановки W₂ и некоторых упрощающих преобразований примет вид:

(2.30)

где f₂ – выходное сечение сопла, м²; P₁, υ₁ – соответственно, давление (Па) и удельный объем (м³/кг) на входе в сопло; 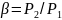– отношение давлений в сопле.

Отношение давлений , при котором расход газа становится максимальным, называется критическим и равно

. (2.31)

Значения в зависимости от k сведены в таблицу 2.1

Значение критической скорости можно найти по формуле

. (2.32)

Таблица 2.1