Перевірочна робота Тема: Співвідношення між тригонометричними функціями одного аргументу. Формули зведення
Варіант 1
1.
Відомо, що sin
=
0,6 і 0 <
<
.
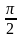Знайти cos
та tg
.
2.
Спростити вираз:
1)
tg2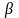
+
sin2
+
cos2
;
2)
.
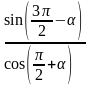3.
Довести тотожність:
.
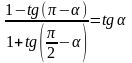Варіант 2
1.
Відомо, що tg
=
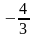і
<
<
.
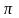Знайти значення трьох інших тригонометричних
функцій кута
.
2.
Спростити вираз: 1)
;
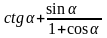2)
.
3.
Довести тотожність:
.
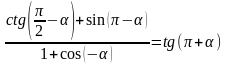Варіант 3
1.
Відомо, що tg
= 3 і
<
<
.
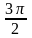Знайти значення трьох інших тригонометричних
функцій кута
.
2.
Спростити вираз: 1)
;
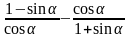2)
tg(
+
)tg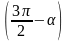
–
sin(
+
)
cos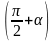
.
3.
Довести тотожність:
.
Перевірочна робота Тема: Співвідношення між тригонометричними функціями одного аргументу. Формули зведення
Варіант 4
1. Відомо, що соs = 0,8 і 0 < < . Знайти sin та tg .
2.
Спростити вираз:
1)
sin2
+
cos2
+
ctg2
; 2)
.
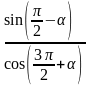3.
Довести тотожність:
.
Варіант 5
1.
Відомо, що ctg
=
і
<
<
.
Знайти значення трьох інших тригонометричних
функцій кута
.
2.
Спростити вираз: 1)
;
2)
.
3.
Довести тотожність:
.
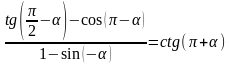Варіант 6
1. Відомо, що ctg = 7 і < < . Знайти значення трьох інших тригонометричних функцій кута .
2.
Спростити вираз: 1)
;
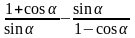2)
ctg(
–
)ctg
+
cos(
–
)
sin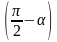
.
3.
Довести тотожність:
.
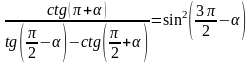Перевірочна робота Тема: Співвідношення між тригонометричними функціями одного аргументу. Формули зведення
Варіант 7
1. Відомо, що sin = 0,6 і 0 < < . Знайти cos та tg .
2. Спростити вираз: 1) tg2 + sin2 + cos2 ; 2) .
3. Довести тотожність: .
Варіант 8
1. Відомо, що tg = і < < . Знайти значення трьох інших тригонометричних функцій кута .
2. Спростити вираз: 1) ; 2) .
3. Довести тотожність: .
Варіант 9
1. Відомо, що tg = 3 і < < . Знайти значення трьох інших тригонометричних функцій кута .
2. Спростити вираз: 1) ; 2) tg( + )tg – sin( + ) cos .
3. Довести тотожність: .
Перевірочна робота Тема: Співвідношення між тригонометричними функціями одного аргументу. Формули зведення
Варіант 10
1. Відомо, що соs = 0,8 і 0 < < . Знайти sin та tg .
2. Спростити вираз: 1) sin2 + cos2 + ctg2 ; 2) .
3. Довести тотожність: .
Варіант 11
1. Відомо, що ctg = і < < . Знайти значення трьох інших тригонометричних функцій кута .
2. Спростити вираз: 1) ; 2) .
3. Довести тотожність: .
Варіант 12
1. Відомо, що ctg = 7 і < < . Знайти значення трьох інших тригонометричних функцій кута .
2. Спростити вираз: 1) ;
2) ctg( – )ctg + cos( – ) sin .
3. Довести тотожність: .
Перевірочна робота Тема: Співвідношення між тригонометричними функціями одного аргументу. Формули зведення
Варіант 13
1. Відомо, що sin = 0,6 і 0 < < . Знайти cos та tg .
2. Спростити вираз: 1) tg2 + sin2 + cos2 ; 2) .
3. Довести тотожність: .
Варіант 14
1. Відомо, що tg = і < < . Знайти значення трьох інших тригонометричних функцій кута .
2. Спростити вираз: 1) ; 2) .
3. Довести тотожність: .
Варіант 15
1. Відомо, що tg = 3 і < < . Знайти значення трьох інших тригонометричних функцій кута .
2. Спростити вираз: 1) ; 2) tg( + )tg – sin( + ) cos .
3. Довести тотожність: .