21. Поперечные и продольные волны. Уравнение бегущей волны.

Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распространения волны. Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т. е. в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах — как продольные, так и поперечные. Бегущими волнами называются волны, которые переносят в пространстве энергию. уравнение бегущей волны.

22.Термодинамические системы и их параметры: давление, температура, объем.

Термодинамической системой — совокупностью макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой). Состояние системы задает­ся термодинамическими параметрами (параметрами состояния) — совокупностью физи­ческих величин, характеризующих свойства термодинамической системы. В ка­честве параметров состояния выбирают температуру, давление и удельный объем. _ Температура — физическая величина, харак­теризующая состояние термодинамического равновесия макроскопической системы. В настоящее время можно применять только две температурные шкалы — термодина­мическую и Международную практическую, градуированные соответственно в кельвинах (К) и в градусах Цельсия (°С). Термодинамическая температура и температура по Между­народной практической шкале связаны соотношением Т = 273,15 + t._ Удельный объем v — это объем единицы массы. Когда тело однородно, т. е. его плотность  = const, то v=V/m=1/p. Так как при постоянной массе удельный объем пропорционален общему объему, то макроскопические свойства однородного тела можно характеризовать объемом тела._ Давление - это силовое воздействие тела и его частей на окружающую среду или оболочку и на соседние части того же тела на единицу поверхности. В системе СИ используется единица давления Паскаль [Па], это 1 Н/м², Для технических измерений паскаль очень маленькая величина, поэтому ввели кратную Паскалю единицу давления бар: 1 бар = 10⁵ Па. В технике часто используется единица давления в старой системе измерения (СГС) - техническая атмосфера 1 атм = 1 кГс/см² (не путать с понятием физической атмосферы).

23 Уравнение Клапейрона — Менделеева

Между давлением р, объемом V и температурой Т существует связь, называемая уравнением состояния

Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: 1) изотермического (изотерма 1–1'), 2) изохорного (изохора 1'–2).

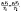
-уравнение Клапейрона, в котором В — газовая постоянная, различная для разных газов.

При одинаковых р и Т моли всех газов занимают одинаковый молярный объем V_m, поэтому постоянная В будет одинаковой для всех газов. Уравнение является уравнением состояния идеального газа, называемым также уравнением Клапейрона — Менделеева. R=8,31 Дж/(мольК). -молярная газовая постоянная

Уравнение Клапейро­на — Менделеева для произвольной массы газа. Если при некоторых давле­нии и температуре один моль газа занимает молярный объем V_m, то при тех же условиях масса т газа займет объем V= (т/М)V_m, где М — молярная масса (масса одного моля вещества)(кг/моль). Уравнение Клапейрона — Менделеева для массы т газа где  =m/M — кол-во вещества. Другая форма уравнения состояния идеального газа, с постоянной Больцмана:

где N_A/V_m = n — концентрация молекул. Из уравнения след. число молекул, содержащихся в 1 м³ газа при нормальных условиях, называется числом Лошмидта*: