Ф1. Кинематическое описание движения материальной точки. Скорость и ускорение.

X=x(t); y=y(t); z=z(t) Уравнение называют кинематическими уравнениями движения точки, записанными в координатной форме. Если они известны, то для каждого момента времени мы сможем рассчитать координаты точки, а следовательно, и ее положение относительно выбранного тела отсчета. Линия, по которой движется точка в пространстве, называется траекторией._ Тела существуют и движутся в пространстве и во времени. Произвольно выбранное тело, относительно которого определяется положение других тел, называется телом отсчета. Совокупность тела отсчета, связанной с ним системы координат и часов, представляет собой систему отсчета.

Рис.1.1

Материальной точкой называется тело, размерами и формой которого можно пренебречь в данной задаче. В декартовой системе координат (рис.1.1) положение материальной точки  А в определенный момент времени, задается тремя координатами x, y, z или радиус-вектором  , проведенным из начала координат O в данную точку A. При движении точки ее координаты изменяются с течением времени. 

Скорость (единица скорости - м/с) — векторная физическая величина, характеризующая быстроту изменения положения тела в выбранной системе отчета. Формула скорости: Быстроту изменения скорости - ускорение. Ускорение - векторная величина, равная первой производной скорости по времени. (еденица ускорения - м/с^2) Формула ускорения: Полное ускорение состоит из двух взаимно перпендикулярных: тангенциального и нормального (центростремительного). Тангенциальное ускорение - направлено по касательной, определяет быстроту изменения модуля скорости. Формула тангенциального ускорения: Нормальное ускорение - характеризует изменение скорости по направлению и совпадает с нормалью к центру кривизны траектории. Формула нормального (центростремительного) ускорения:

2. Скорость и ускорение при криволинейном движении.

При криволинейном движении вектор скорости всегда направлен по касательной к траектории движения. Любое криволинейное движение можно представить в виде суммы прямолинейных движений и движений по окружностям разных радиусов.Скорость изменяется как по величине, так и по направлению. Вектор ускорения направлен под углом к вектору скорости. При криволинейном движении точки направление ее скорости все время изменяется, а модуль скорости может как изменяться, так и оставаться постоянным. Криволинейное движение всегда движение ускоренное._ Направление ускорения при криволинейном движении не совпадает с направлением скорости. Чтобы найти направление ускорения при криволинейном движении, достаточно сопоставить направления скоростей в двух близких точках траектории. Так как скорости направлены по касательным к траектории, то по виду самой траектории можно сделать заключение, в какую сторону от траектории направлено ускорение. Действительно, так как разность скоростей   в двух близких точках траектории всегда направлена в ту сторону, куда искривляется траектория, то, значит, и ускорение всегда направлено в сторону вогнутости траектории. 

3. Связь между угловой и линейной скоростями при вращении твердого тела вокруг неподвижной оси Связь между линейной и угловой скоростями. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости._ При вращении твердого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова. Между линейной скоростью любой точки вращающегося тела и его угловой скоростью существует связь. Установим ее. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь  . Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так: Так как  , то

Угловой скоростью называется вектор  , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении (  и   всегда направлены в одну сторону).

Если  ω – const, то имеет место равномерное вращение тела вокруг неподвижной оси. Пусть  v  – линейная скорость точки М. За промежуток времени dt точка М проходит путь dr = vdt. В то же время  dr = Rdφ  (dφ - центральный угол). Тогда, можно получить связь линейной скорости и угловой: . В векторной форме Наряду с угловой скоростью вращения используют понятия периода и частоты вращения. _Период Т – промежуток времени, в течение которого тело совершает полный оборот (т.е. поворот на угол φ = 2π). _ Частота ν – число оборотов тела за 1 секунду. _При вращении с угловой скоростью ω имеем: , , . Вектор углового ускорения  для характеристики неравномерного вращения тела: .

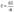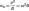
4) Законы Ньютона. Масса. Сила

В основе классической динамики (основной раздел механики) лежат три закона Ньютона. Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции. Первый закон Ньютона выполняется не во всякой системе отсчета, а те системы, по отношению к которым он выполняется, называются инерциальными системами отсчета. Второй закон Ньютона — основной закон динамики поступательного движения — отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил. р = mv - импульс

второй закон Ньютона: скорость изменения импульса материальной точки равна действующей на неесиле. Выражение называется так же уравнением движения матери-

альной точки. Третий закон Ньютона. силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены формула с модулем только без минуса. _Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства._ Сила — это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.

5)Силы в механике: трение, тяготение.

Сила трения. Всякое тело, движущееся по горизонтальной поверхности другого тела, при отсутствии действия на него других сил с течением времени замедляет свое движение и в конце концов останавливается. Это можно объяснить существованием силы трения, которая препятствует скольжению соприкасающихся тел относительно друг друга. Различают внешнее (сухое) и внутреннее (жидкое или вязкое) трение. Внешним трением называется трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении. Внутренним трением называется трение между частями одного и того же тела, например между различными слоями жидкости или газа, скорости которых меняются от слоя к слою. f- коэффициент трения скольжения. Р=mg; ma = mg + N + Fтр; ma = mgsin a – Fтр = mgsin a - fmgcos a; Fтр = fmgcos a. При a = 0: mgsin a = fmgcos a; f = sin a/cos a = tg a

6) Закон всемирного тяготения: между любыми двумя материальными точками действует сила взаимного притяжения, прямопропорциональная произведению масс

этих точек (m1 и m2) и обратно пропорциональная квадрату расстояния между ними (r^2): . Эта сила называется гравитационной (или силой всемирного тяготения). Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через взаимодействующие тела. Коэффициент пропорциональности G называется гравитаци­онной постоянной. Значение G принимается равным 6,672010^–11 Нм/кг², т. е. два точечных тела массой по 1 кг каждое, находящиеся на расстоянии 1 м друг от друга, притягиваются с силой 6,672010^–11 H. Очень малая величина G показывает, что сила гравитационного взаимодействия может быть значительной только в случае больших масс._ Закон всемирного тяготения установлен для тел, принимаемых за материальные точки, т. е. для таких тел, размеры которых малы по сравнению с расстоянием между ними.