25.Случайные величины. Дискретные случайные величины. Закон и функция распределения.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперёд не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Случайные величины обозначаются буквами X, Y, Z, … , а их возможные значения соответственно x, y, z, ….

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Закон распределения дискретной случайной величины – это перечень всех возможных значений дискретной случайной величины и соответствующих вероятностей. Сумма всех вероятностей Σp_i = 1.

Закон распределения (закон случайной величины) можно задать аналитически (при помощи формулы) и графически (при помощи многоугольника распределения, который соединяет точки (x_i; p_i).

 Функция распределения случайной величины - это вероятность того, что случайная величина (пусть она будет ξ) будет принимать значение меньшее, чем заданное числовое значение x:

F(X) = P(ξ < X).

 У дискретной случайной величины функция распределения случайной величины вычисляется для всех значений как сумма вероятностей, которые соответствуют каждому предшествующему значению случайной величины.

26.Случайные величины. Непрерывные случайные величины. Функция и плотность распределения вероятностей непрерывной случайной величины.

Непрерывной случайной величиной называется случайная величина, все возможные значения которой целиком заполняют некоторый промежуток на числовой прямой.

Функция распределения непрерывной случайной величины: 

Функция не убывает и непрерывна, причем производная функции не имеет разрывов на всей числовой оси, за исключением конечного числа точек.

Плотностью вероятности (Плотностью распределения или Плотностью) Р(Х) непрерывной случайной величины Х называется производная ее функции распределения

.

Плотность вероятности Р(Х), как и функция распределения F(Х), является одной из форм закона распределения, но в отличие от функции распределения она существует только для Непрерывныхслучайных величин.

Плотность вероятности иногда называют дифференциальной функцией, или дифференциальным законом распределения.

График плотности вероятности называется кривой распределения.

Свойства плотности вероятности непрерывной случайной величины:

.

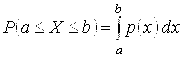 (рис. 8.1).

 

.

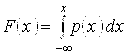
Геометрически свойства плотности вероятности означают, что ее график — кривая распределения — лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.