Формула Байеса

При выводе формулы полной вероятности предполагалось, что вероятности гипотез известны до опыта. Формула Байеса позволяет производить переоценку первоначальных гипотез в свете новой информации, состоящей в том, что событие произошло. Поэтому формулу Байеса называют формулой уточнения гипотез.

Теорема (Формула Байеса).Если событие может происходить только с одной из гипотез  , которые образуют полную группу событий, то вероятность гипотез при условии, что событие произошло, вычисляется по формуле

,  .

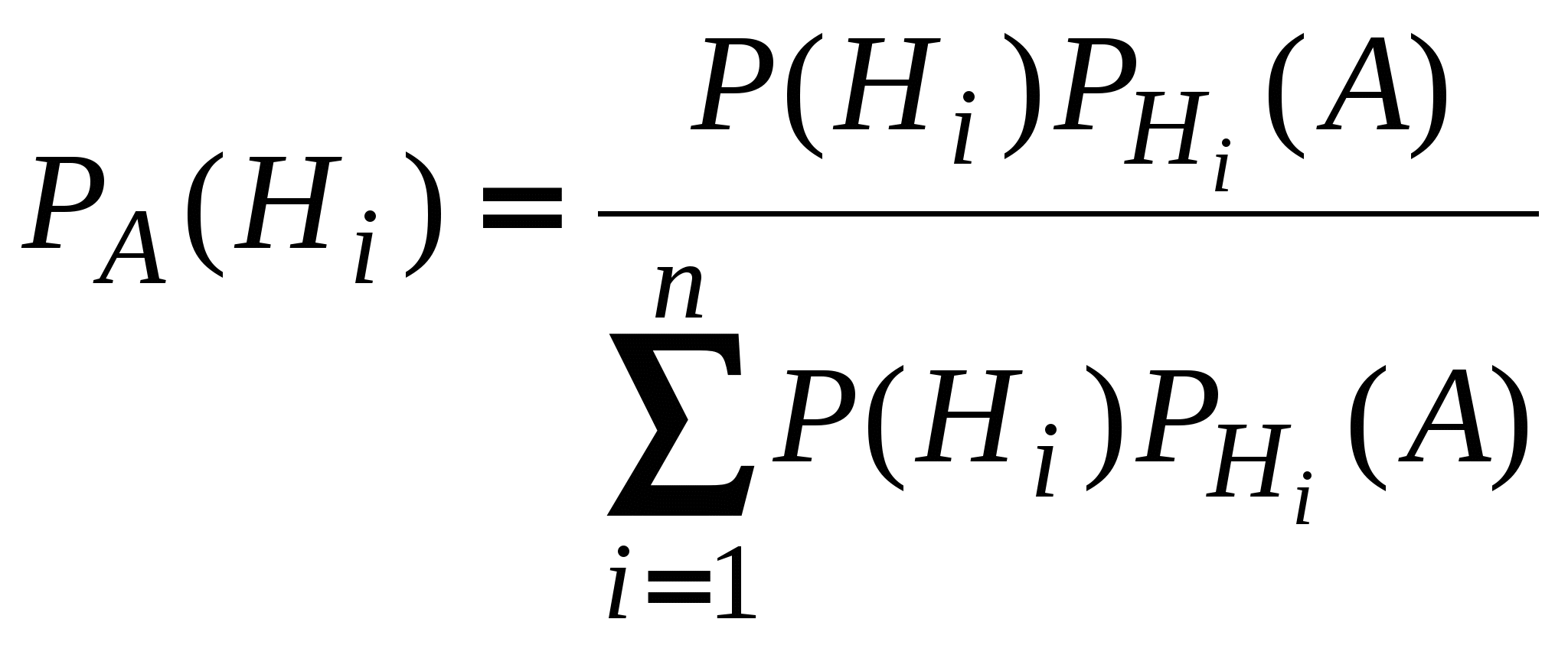Доказательство.

Формула Байеса или байесовский подход к оценке гипотез играет важную роль в экономике, т.к. дает возможность корректировать управленческие решения, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе и.т.п.

Пример.Электролампы изготовляются на двух заводах. Первый завод производит 60% общего количества электроламп, второй – 40%. Продукция первого завода содержит 70% стандартных ламп, второго – 80%. В магазин поступает продукция обоих заводов. Лампочка купленная в магазине оказалась стандартной. Найти вероятность того, что лампа изготовлена на первом заводе.

Запишем условие задачи, вводя соответствующие обозначения.

Дано:событие состоит в том, что лампа стандартная.

Гипотеза  состоит в том, что лампа изготовлена на первом заводе

.

Гипотеза  состоит в том, что лампа изготовлена на втором заводе

.

23.Повторные независимые испытания. Формулы Бернулли, Пуассона.

На практике приходится сталкиваться с такими задачами, которые можно представить в виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появиться событие  . При этом интерес представляет исход не каждого "отдельного испытания, а общее количество появлений события в результате определенного количества испытаний. В подобных задачах нужно уметь определять вероятность любого числа появлений события в результате испытаний. Рассмотрим случай, когда испытания являются независимыми и вероятность появления события в каждом испытании постоянна. Такие испытания называются повторными независимыми.

Примером независимых испытаний может служить проверка на годность изделий, взятых по одному из ряда партий. Если в этих партиях процент брака одинаков, то вероятность того, что отобранное изделие будет бракованным, в каждом случае является постоянным числом.

Формула Бернулли

, а повторяющиеся испытания, удовлетворяющие условию независимости и постоянства вероятностей появления в каждом из них события, называютиспытаниями Бернулли, илисхемой Бернулли.

24.Повторные независимые испытания. Локальная и интегральная формулы Муавра-Лапласа.

ЛОКАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА

Вероятность того, что в   независимых испытаниях с вероятностью появления события   равной   событие   наступит ровно   раз (безразлично в какой последовательности) определяется по приближенной формуле

где

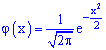– Функция Гаусса,

– аргумент функции Гаусса;

– вероятность противоположного события  .

Формулу   называют локальной формулой Лапласа.

Функция  обладает следующими свойствами:

1) она является четной функцией  ;

2) для значений аргумента больше четырех она сколь угодно мала 

Теорему Лапласа рекомендуется применять при значениях произведения больше девяти

ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА-ЛАПЛАСА

Вероятность, что в   независимых испытаниях событие   с вероятностью появления   наступит не менее  раз и не более   (независимо от последовательности появления) приближенно определяется зависимостью

где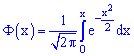 – интегральная функция Лапласа;

– аргументы интегральной функции распределения;

 – вероятность невыполнения события  .

Функция   обладает следующими свойствами:

1) она является нечетной функцией

2) для аргументов больше пяти она равна 0,5

Значение обеих функций   находят из таблиц в которых функции с достаточной точностью протабульовани.

--------------------------------