12. Методы вычисления определенного интеграла: непосредственное

интегрирование. Формула Ньютона-Лейбница.

Для вычисления определенного интеграла от непрерывной на отрезке [a;b] функции f(x) в том случае, когда может быть найдена ее первообразная F(x) служит формула Ньютона-Лейбница:

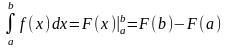
т.е. определенный интеграл равен разности значений любой первообразной при верхнем и нижнем пределах интегрирования.

При интегрировании четных и нечетных функций в симметричных пределах интегрирования используют формулу:

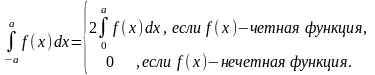
13.Методы вычисления определенного интеграла: метод подстановки. Замена переменной в определенном интеграле требует замены пределов ингрирования:

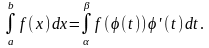
Условия использования :

1. Функция f(x) непрерывна на отрезке [a,b]

2. Отрезок [a,b] есть множество значений функции x= (t), имеющей непрерывную производную

14.Примеры применения определенного интеграла для решения задач физики,

химии, биологии

стр. 73-77

15.Дифференциальные уравнения, их виды. Общее и частное решения

дифференциальных уравнений. Уравнения с разделяющимися переменными.

Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию y=f(x), и ее производные или дифференциалы.

Дифференциальное уравнение называется обыкновенным, если искомая функция y=f(x) зависит от одного независимого переменного.

Если независимых переменных две и больше, то уравнение называется дифференциальным уравнением в частных производных.

Процесс нахождения решений дифференциального уравнения называется интегрированием этого уравнения.

Общим решением (или общим интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную y=φ(x, C).

Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных.

Дифференциальное уравнение вида 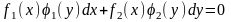, в котором коэффициенты при дифференциалах распадаются на произведение множителей, каждый из которых зависит только от x или только от y, называется уравнением с разделяющимися переменными.

16.Решение линейных дифференциальных уравнений второго порядка с

постоянными коэффициентами.

17. .Дифференциальные уравнения в биологии, физике, химии. Примеры.

Cтр.105-109

18.Комбинаторика: сочетания, размещения, перестановки, правила суммы и произведения

В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).

Определение. Размещениями множества из   различных элементов по   элементов   называются комбинации, которые составлены из данных   элементов по   элементов и отличаются либо самими элементами, либо порядком элементов.

Число всех размещений множества из   элементов по   элементов обозначается через   (от начальной буквы французского слова “arrangement”, что означает размещение), где   и  .

Теорема. Число размещений множества из   элементов по   элементов равно

Определение. Перестановкой множества из   элементов называется расположение элементов в определенном порядке.

Так, все различные перестановки множества из трех элементов   — это

Очевидно, перестановки можно считать частным случаем размещений при  .

Число всех перестановок из   элементов обозначается   (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле

Определение. Сочетаниями из   различных элементов по   элементов называются комбинации, которые составлены из данных   элементов по  элементов и отличаются хотя бы одним элементом (иначе говоря,  -элементные подмножества данного множества из   элементов).

Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из   элементов по   элементов в каждом обозначается   (от начальной буквы французского слова “combinasion”, что значит “сочетание”).

Числа