Функция. Способы ее задания. Четность, нечетность, область определения. Классы основных элементарных функций.
Числовой функцией называется соответствие, которое каждому числу х из некоторого заданного множества сопоставляет единственное число у.
Графиком функции называется множество точек плоскости с координатами (x, f(x))
Способы задания функции:
аналитический способ (с помощью математической формулы);
табличный способ (с помощью таблицы);
описательный способ (с помощью словесного описания);
графический способ (с помощью графика)
Функция называется четной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = f(x)
График четной функции симметричен относительно оси 0y
Функция называется нечетной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = –f(x)
График нечетной функции симметричен относительно начала координат.
Множество значений x называется областью определения функции (обозначается D(f))
Классы основных элементарных функций:
Степенная функция (
,
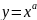где а- действительное число)Показательная функция (
,
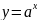где a- положительное
число, не равное 1)Логарифмическая функция (у=
,
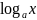где а-положительное число, не равное
1)Тригонометрические функции (у=sinx, y=cosx, y=tgx,y=ctgx)
Обратные тригонометрические функции( y= arcsinx, y=arccosx)
Производная функции в точке и на интервале, ее алгебраический, механический и геометрический смысл.
Если
существует предел отношения приращения
функции к приращению аргумента при
условии, что приращение аргумента
,
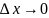то он называется значением производной
функции f(x)
в точке
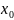
Если в точке x0 существует конечная производная функции y=f(x), то эта функция называется дифференцируемой в точке x0.
Если функция y=f(x) дифференцируема в каждой точке некоторого промежутка, то она дифференцируема на промежутке.
Алгебраический смысл: производная функции в точке есть угловой коэфициент касательной к графику этой функции
Геометрический смысл: угловой коэффициент касательной, приведенной к графику функции y=f(x) в точке x0 равен значению производной функции в этой точке.
Механический смысл: скорость тела равна первой производной координаты по времени:
V(t)=x / (t).
Соответственно, вторая производная функции – скорость изменения скорости, т.е. ускорение:
a(t)= V / (t)=x // (t).
3. Правила нахождения производных. Таблица производных. Производная
сложной функции.
Правила нахождения производных
1. (с*u) ′=с*u′, с=const (постоянный множитель можно выносить за знак производной)
2. Производная суммы двух дифференцируемых функций равна сумме их производных:
(u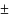
v)
′ =u′
v′
3. Производная
произведения двух дифференцируемых
функций вычисляется по следующему
правилу: (uv) ′=u′v+uv
4. Производная частного двух дифференцируемых функций вычисляется по следующему правилу:
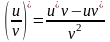
Таблица производных
Производная сложной функции
4. Дифференциал функции, его алгебраический и геометрический смысл.
Свойства дифференциала.
Дифференциал функции равен произведению производной функции на приращение ее аргумента.
Дифференциал функции есть главная часть приращения функции. В этом состоит аналитический смысл дифференциала
Геометрический смысл: дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
Свойства дифференциала: аналогичны свойствам производной.