Министерство образования Российской Федерации

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ ( ТУСУР )

Кафедра промышленной электроники Лабораторная работа №1

По дисциплине “ Метрология ”

Дата выполнения работы ________________________________

Номер варианта _______________________________________

Дата проверки __________________________________________

Оценка _________________________________________________

ФИО преподавателя _____________________________________

Подпись преподавателя __________________________________

Цель работы : Целью данной работы является изучение методических погрешностей при прямых и косвенных измерениях .

1. Прямые измерения .

Используя пакет Electronics Workbench реализуем схему измерения постоянного тока , потребляемого активной нагрузкой .

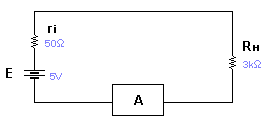Ток, измеряемый амперметром в этом случае , есть действительное значение тока нагрузки и составляет Iд=Е/(ri+Rн)=1.639 мА . В этой ситуации реализуется идеальный измерительный эксперимент . Т.е. было учтено внутреннее сопротивление источника питания, но для измерения тока нагрузки реальным амперметром нам необходимо учесть сопротивление самого прибора . Для этого включим последовательно с амперметром сопротивление , эмитирующие сопротивление прибора R_А . Для начала возьмем R_А =0.1R_Н = 3*0.1=0.3 кОм=300 Ом.

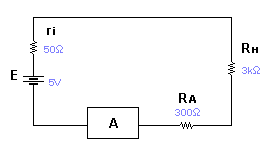Произведя повторное измерение , амперметр показал следующее значение 1.492 мА. Показание прибора в этом случае – значение ток нагрузки измеренное реальным прибором .

Измеренное значение тока I_А=Е/(R_H+ri+R_A) =

5/(3000+50+300)=1.492 мА.

Абсолютное значение методической погрешности измерения тока

∆I _мет=I_A-I_д=1.492-1.639=-0.147. Относительная методическая погрешность измерения тока δI_мет=∆I_мет/I_д=

-0.147/1.639=-0.089. Относительная погрешность может быть выражена в % если полученное безразмерное число умножить на 100 т.е. δ_х[%]= *100%=

= (-0.147/1.639)*100=-8.96 . Данную погрешность можно отнести к методической т.к. она обусловлена не идеальностью амперметра , т.е. сопротивление амперметра R_А ≠ 0.

Изменяя сопротивление амперметра R_А от R_А=0.1R_H до R_A=R_H найдем относительные погрешности . Для наглядности полученные результаты занесем в таблицу .

Iд мА	IА мА	∆Iмет=IA-Iд	δIмет =∆Iмет/Iд		RA Ом	RA /RH
			числ	*100%
1.639	1.492	-0.147	-0.089	-8.96	300	0.1
1.639	1.408	-0.231	-0.14	-14.09	500	0.166
1.639	1.234	-0.405	-0.24	-24.71	1000	0.333
1.639	1.099	-0.54	-0.32	-32.94	1500	0.5
1.639	0.99	-0.649	-0.39	-39.59	2000	0.66
1.639	0.901	-0.738	-0.45	-45.02	2500	0.833
1.639	0.826	-0.813	-0.49	-49.6	3000	1

По полученным данным построим график зависимости методической погрешности от соотношения R_А / R_H т.е. δ_Iмет [%]=f(R_A /R_H)

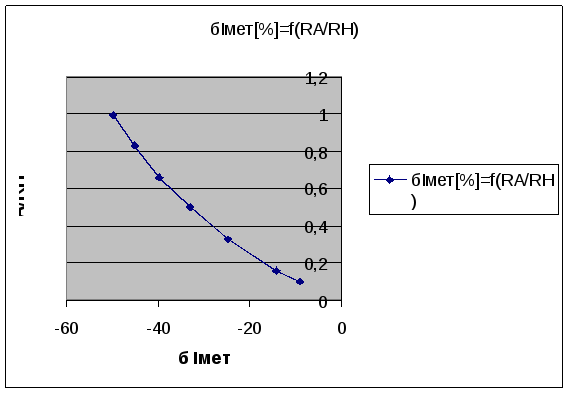
Исходя из графика можно сделать вывод , что методическая погрешность практически линейно зависит от сопротивления амперметра . Критерием , когда методическую погрешность можно не учитывать , может служить δ_Iмет≤ δ_Iосн/ 5 где δ_Iосн – основная погрешность амперметра , определяемая его классом точности . Если предположить что класс точности прибора 1.0 . Тогда 1/5=0.2 .Следовательно методическую погрешность можно не учитывать в том случае если соблюдается условие R_А /R_H =0.2/100. Исходя из этого найдем максимально допустимое сопротивление амперметра R _{А /} 3000=0.2/100 =6 Ом .Таким образом для измерения сопротивления в 3000 Ом , сопротивление амперметра не должно превышать 6 Ом .

В этом случае методическая погрешность может не учитываться .

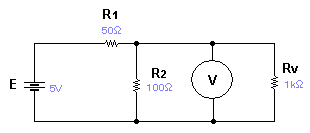
Реализуем на экране компьютера ситуацию измерения падения напряжения постоянного тока на участке электрической цепи .

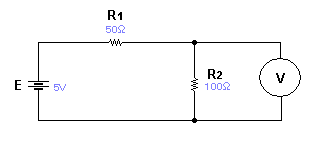При указанных значениях элементов , вольтметр покажет 3.33 В. В данной схеме мультиметр используется в режиме измерения напряжения постоянного тока и представляет собой идеальный вольтметр , внутренние сопротивление которого Rv= ∞ . Произведем аналогичное измерение реальным вольтметром . Для этого параллельно вольтметру включим сопротивление Rv , имитирующее внутренние сопротивление реального вольтметра .Для начала возьмем Rv= 10Ri , где Ri- сопротивление участка цепи на котором производится измерение .

В такой схеме показание вольтметра будут ровняться 3.226 В. Как видно показания прибора отличаются от предыдущих . Следовательно необходимо найти погрешность измерения . Абсолютная погрешность ∆U=U_д-U_изм = 2.5-3.33=∆U=-0.83

Относительная погрешность δ_х=∆U/U_дст=-0.83/3.33=-0.24

Произведем измерения изменяя величину Rv от Rv=Ri до Rv=100Ri и полученные данные, как и в предыдущих измерениях занесем в таблицу .

Uд В	Uизм В	∆U = Uизм -Uд	δuмет =∆U/Uдст		Rv oM	Ri /Rv
			числ	*100%
3.333	2.5	-0.83	-0.24	-24.92	100	1
3.333	3.261	-0.07	-0.021	-2.1	1500	0.066
3.333	3.291	-0.04	-0.01	-1,2	3000	0.033
3.333	3.309	-0.021	-0.006	-0.63	4500	0.022
3.333	3.315	-0.015	-0.004	-0.45	6000	0.016
3.333	3.319	-0.011	-0.003	-0.33	7500	0.013
3.333	3.321	-0.009	-0.002	-0.27	9000	0.011

По полученным данным построим график зависимости методической погрешности от соотношения δ_Uмет [%]= f(Ri/Rv)

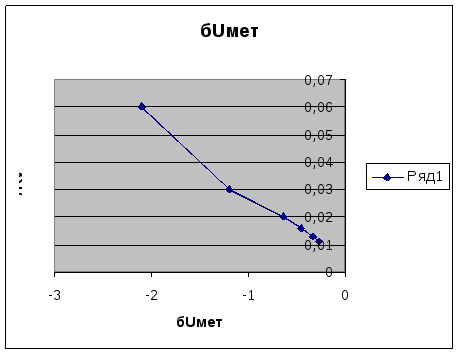
Исходя из результатов измерений и графика видно , что в эксперименте измерения напряжения ситуация выглядит с точность наоборот нежели в измерениях тока . Т.е чем выше сопротивление прибора тем точнее измерение . Если сопротивление вольтметра Rv увеличить до 60 -80 кОм , то действительная величина Хдст ≈ Хизм . . Критерием , когда методическую погрешность можно не учитывать , может служить δ_Iмет≤ δ_Uосн/ 5 где δ_Uосн – основная погрешность вольтметра . Таким образом если класс точности прибора 1.0 , то δ<=δ_Uосн/5 =0.2 . Определим минимально допустимое сопротивление вольтметра 100/Rv=0.2/100=50000 . Отсюда для измерения сопротивления в 100 Ом минимальное сопротивление вольтметра не должно быть ниже 50 кОм . В этом случае методическую погрешность можно не учитывать.