Тарировка термопары

Прежде чем приступить к экспериментам, термопару следует тарировать, т.е. установить зависимость между температурою резца и показателями милливольтметра. Тарировочное устройство состоит из электропечи, ванны для плавки алюминия, контрольного термометра, соединительных проводов, гальванометра, твердосплавной пластинки и пластинки из материала заготовки. В ванну с расплавленным алюминием погружают пластинку из обрабатываемого материала, резец с твердосплавной пластинкой и контрольный термометр (рис. 13.6.). Пластинку и резец соединительными проводами соединяют с гальванометром. При нагреве ванны записывают показания контрольного термометра и показания гальванометра. По результатам показаний строится тарировочный график θ = f(n) . Естественная термопара обеспечивает удовлетворительные результаты, но требует относительно сложного тарирования, т.к. для каждого вида обрабатываемого материала и материала резца необходимо строить отдельные тарировочные графики.

Рис. 13.6. Схема установки для тарировки термопары.

1 - ванночка для металла; 2 - расплавленный металл; 3 - пластина из материала заготовки; 4 - твердосплавная пластина резца; 5 -электропровода; 6 -гальванометр; 7 -теомометр.

Рис. 13.7. Тарировочный график естественной термопары

Порядок выполнения работы

1. Установить стальную заготовку в станок при этом один конец жестко закрепить в патроне, а второй подпереть центром задней бабки.

2. Установить резец в резцедержатель или проверить правильность его установки.

3. Провести тарировку естественной термопары по ранее изложенной методике.

4. Штангенциркулем в месте точения измерить диаметр заготовки.

5. Настроить станок для проведения трех серий опытов, но при этом учесть, что в первой серии величина подачи и глубина резания постоянные, а измеряем величину скорости резания, во второй серии скорость и глубина постоянные, а измеряем величину продольной подачи, в третьей серии скорость и подача постоянные, а измеряем глубину резания.

Результаты опытов и исходные данные записываем в таблицу.

6. Определить скорость резания при точении V, м/мин по формуле:

(13.4)

где D - диаметр заготовки, мм; n - число оборотов шпинделя, об/мин.

7. Используя данные таблицы построить в логарифмической системе координат график зависимости температуры в зоне резания θ от скорости резания V, график зависимости температуры в зоне резания θ от подачи S и график зависимости температуры в зоне резания θ от глубина резания t.

Математическое выражение приведенных графических зависимостей записывается как:

lg θ = lgC_θ1 + Z_θ · lgV, (13.5)

Igθ = lgC_θ2+Y_θ· lgS, (13.6)

Igθ = lgC_θ3+X_θ·lgt, (13.7)

Выражения (68), (69) и (70) являются уравнениями первой степени. Показатели степени Z_θ, Y_θ и Х_θ численно равны тангенсу угла наклона прямых линий.

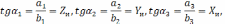
Отрезки прямых a₁b₁ a₂b₂ и a₃b₃ пересекающие линию наклона в направлении осей координат выбирают произвольно. Замерив значения этих отрезков, которые представляют катеты прямоугольных треугольников, подсчитывают значения Z_θ, Y_θ и Х_θ. Коэффициенты С_θ1 С_θ2 и С_θ3 зависят от свойств обрабатываемого материала и условий обработки. Из логарифмических уравнений (13.5), (13.6) и (13.7) следует, что

θ = С_θ1, · V^Zθ, θ= С_θ2 · S^Yθ, θ= С_θз · t^Xθ. (13.8)

В общем виде зависимость температуры в зоне резания θ от скорости резания V, подачи S и глубины резания t будет иметь вид

θ = С_θ · V^Zθ · S^Yθ · t^Xθ, (13.9)

где; Z_θ, Y_θ и Х_θ - показатели степеней; С_θ - коэффициент, зависящий от физико-механических свойств обрабатываемого материала и условий обработки.

Численное значение коэффициента С₉ определяется решением уравнения (13.9). Для этого значения θ, V, S и t берут из таблицы, а значения степеней Zθ, Yθ и Хθ из построенных графиков или полученных аналитическим путем (порядок расчета приводится ниже).

Решение функции (13.4) аналитическим способом:

8. Определить показатели степени Zθ, Yθ и Хθ, решив уравнения (13.5), (13.6) и (13.7).

Из таблицы берем значения θ и V и подставляем в уравнение (13.5):

(13.10)

Решением уравнения (13.10) для трех опытов первой серии получим значения Z_θ1, Z_θ2, Z_θ3.

9. Определить среднее значение Z_Θcp.

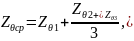
(13.11)

9. Из таблицы берем значения θ и S подставляем в уравнение (13.6)

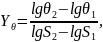
(13.12)

Решением уравнения (13.12) для трех опытов второй серии получим значения Y_θ1, Y_θ2, Y_θ3.

9. Определить среднее значение Y_θсp.

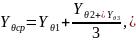
(13.13)