
- •1.1. Материалдардың беріктік және созымдылық физикасы пәнінің мәні мен мақсаты.
- •2.1. Беріктік және созымдылық, негізгі түсініктер мен анықтамасы.
- •2.2. Мартенситті беріктендірудің физикалық мәні.
- •2.3. Шаршауға қарсыластылықты анықтайтын негізгі жағдайлар мен факторлар
- •3.1. Созымдылық және деформация. Деформацияның түрлері.
- •3.2. Беріктікті анықтайтын әдістер. Беріктік қасиетті бағалау критерийі.
- •3.3. Металдар мен қорытпалардың суықтай сынғыштығы.
- •Кернеу тензоры. Гуктың элементарлық заңы.
- •Атомаралық байланыстың тез (Гриффитс бойынша) және бірізді үзілуі жағдайында қирауы.
- •3. Беріктіктің классикалық теориясы. Механикалық беріктіктің энергетикалық және деформациялық критерийлері.
- •Созымдылық және деформация.Созымдылық – материалдардың деформациялануға қабілеттілік критерийі ретінде.
- •Жылжыпсырғымалылық. Анықтамалары мен мәні.
- •Легірлеу кезіндегі беріктікті жоғарылатудың физикалық мәні мен тәсілдері.
- •1. Материалдардың механикалық қасиеттері қандай заңға бағынады?
- •2. Аса созымдылықтың теориялық негізі. Аса созымдылық деформациясының моделі.
- •2. Қирау. Жоғары температуралар кезіндегі қирау.
- •2. Кернеу. Кернеу түрлері.
- •2. Созымдылықтың температуралық аномалиясы. Жылулық сынғыштық мәселелері және оны шешу келешегі.
- •3. Кирау. Кираудың түрлері мен белгілері.
- •1. Беріктік және созымдылық, негізгі түсініктері мен анықтамалары.
- •3. Кернеу түрлері және кернеу тензоры.
- •1. Материалдардың мортты кирауы кезіндегі беттік энергияның мәні.
- •3. Ыстыққа беріктіктің статикалық беріктіктен айырмашылығы неде.
- •2. Деформация. Шартты және шынайы деформация.
- •3. Серпімділік модулі, мәні мен анықталуы.
- •1. Созымдылық пен беріктік қасиеттерінің сипаттамалары.
- •2. Аса беріктіктің теориялық негізі. Аса беріктік түрлері.
- •3. Материалдардың жоғары беріктік күйін жасаудың физикалық және құрылымдық факторлары.
- •1. Мортты қираудағы созымды деформацияның атқаратын ролі.
- •2. Металдар мен қорытпалардың қайтакристалдану және балқу температуралары арасында қандай байланыс бар.
- •3. Жылжыпсырғымалылықтың әр сатысында дамитын процестер.
- •1. Шаршауға беріктікті жоғарылату тәсілдері.
- •2. Жылжыпсырғымалылық кезіндегі созымдылық туралы түсінік.
- •3. Статикалық беріктікті анықтайтын тәжірибелер.
- •19 Билет
- •1. Беріктікті анықтау әдістері.Беріктік қасиеттерді бағалау критерийлері.
- •2.Морт қирау-беріктіктің катастрофиялық жойылуы
- •3. Қатты денелер беріктігінің уақытша тәуелділігі
- •20 Билет
- •1. Жылжыпсырғымалылық. Ақаулардың жинақталуы.
- •2. Созымды деформация физикасы мен геометриясының негізі. Созымды жылжу геометриясы.
- •3.Материалдардың шекті күйі
- •21 Билет
- •1. Беріктікті анықтау әдістері.Беріктіктің класскалық теориясы
- •2.Металдар мен қорытпалардың созымдылығы мен қирауының пайда болуы
- •3.Металдық байланыс энергиясының физикалық табиғаты
- •1. Мартенситтің жоғары беріктігін алу тәсілдері.
- •2. Аса беріктіктің теориялық негізі. Аса беріктік түрлері.
- •1. Конструкциялардың негізгі қабілеттілігіне материалдардың қатаңдығының ықпалы.
- •2. Шынайы деформацияның физикалық мәні.
- •3. Динамикалық беріктікті анықтау тәсілдері.
- •1. Мартенситті беріктендірудің физикалық мәні.
- •2. Деформация түрлері. Шынайы және шартты деформация мәнін түсіндіріңіз.
- •3. Біртекті деформация қандай себептермен созымдылық шаралары ретінде есептеулерде қолданылады.
- •25.Билет
- •26 Билет
- •27 Билет
- •1. Материалдардың механикалық қасиеттеріне созымды деформацияның ықпалы.
- •2. Беріктікті анықтау әдістері. Беріктіктің классикалық теориясы.
- •3. Серпімділік модулі, мәні мен анықталуы.
- •1. Жылжыпсырғымалылық кезіндегі созымдылық туралы түсінік.
- •2. Динамикалық беріктікті анықтау тәсілдері.
- •3. Созымды деформация физикасы мен геометриясының негізі. Созымды жылжу геометриясы.
- •1. Металдар мен қорытпалардың қайтакристалдану және балқу температуралары арасында қандай байланыс бар.
- •2. Статикалық беріктікті анықтау тәсілдері.
- •3. Жылжыпсырғымалылық. Ақаулардың жинақталуы.
Кернеу тензоры. Гуктың элементарлық заңы.
Кернеу тензоры.Осындайтүрде есептелген кернеу жүктелген біртекті қатты дененің интегралды сипаттамасы болып табылады. Оның кезкелген нүктесіндегі кернеулік күйді білу үшін осы нүктенің жан-жағына шексіз аз тікбұрышты параллелепипед тұрғызады, оның қыры х, у, z координатасында тікбұрышты жүйе түзеді (2.3,б-сурет). Параллелепипедтің үш параллель емес қырына әсер ететін кернеудің әр қайсысы бір нормальды және екі жанаспалы құрауышқа түсуі мүмкін. Нормальды кернеу бағытын анықтайтын индекс осы қырға перпендикуляр осьтің белгіленуіне сәйкес келеді. Жанаспалы кернеу үшін бірінші индекс мәні нормальдыға сәйкес, ал екіншісі осы кернеу әсер ететін ось белгісіне сай келеді.
|
|
2.3-сурет. Нүктедегі толық кернеу (а) мен кернеулік күйді анықтаудың (б)қойылутәсілінің көрініс схемасы |
|
Жүктелген дененің барлық нүктесіндегі кернеулік күйді анықтайтын нормальды және жанаспалы кернеулердің жинағы кернеу тензорын түзеді. Сонымен нүктедегі кернеулік күй тоғыз шамамен сипатталады және де мынандай матрица түрінде жазылады
(S)
=

Кернеу тензорын құрайтын тоғыз компоненттен тек алтауы ға тәуелсіз болып табылады. Қарастырылатын параллелепипедтің тепе-теңдік жағдайынан (кез келген оське қатысты суммалық айналмалы момент нөльге тең болуы тиіс) txy = tyx, txz = tzx, tyz = tzyшығаруға болады, демек, тензордың басты диагоналына (S–S) қатысты симетриялы компоненттер өзара тең.
Жанаспалы кернеу нөлге тең координата жүйесін таңдау кезінде кернеу тензоры мынадай түрде болады
 ,
,
S1> S2> S3 деп алады, және де осы кернеулерді басты кернеулер деп атайды.
(2.5) теңдеуіне сәйкес максимальды жанаспалы кернеу басты нормальды кернеуге сәйкес келетін жартылай айырмашылыққа, демек, басты жанаспалы кернеугетең.
 ;
;  ;
;  .
.
Гуктың элементарлық заңы
Серпімділік дегеніміз деформацияланатын күштің әсері жойылғаннан кейінгі өзінің пошымы мен көлемін (қатты дене) немесе тек көлемін қайтадан орнына келетін материалдың қасиеттері аталады. Металдың серпімділік түсінігінің заңдылықтарын алғаш рет ағылшын оқымыстысы Гук 1678 жылы ашты. Оны былай түсіндіреміз:
Үлгінің тұрақты ұзындығы (l) және қимасы кезінде (F) оның ұзындығының өсуі жүктемеге тік пропорционалды
 .
.Жүктеме (P) мен қиманың тұрақты кезінде ұзындықтың өсуі үлгінің алғашқы ұзындығына тік пропорционалды
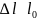 .
.
Маңызды тәжірибелік факт: үлгі қаншалықты ұзын болса, соншалықты ол бірдей әсер ететін жүктеме кезінде ұзарады.
Тұрақты жүктеме және бастапқы ұзындығы кезінде үлгінің ұзындығының өсуі оның ауданына кері пропорционал
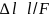 .
.Тұрақты жүктеме, бастапқы ұзындық және аудан кезінде үлгінің ұзындығының артуы оны дайындаған материалға тәуелді.
Сондықтан, созылудың серпімділік аймағына келесі өрнекбелгіге сай:
 (2.4)
(2.4)
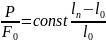 (2.5)
(2.5)
 (2.6)
(2.6)
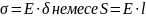
Осы теңдеу Гуктың теңдеуі немесе Гуктың элементарлық заңы деп аталады.
Атомаралық байланыстың тез (Гриффитс бойынша) және бірізді үзілуі жағдайында қирауы.
Морт қираудың қирау теориясы негізінен Гриффитс тапқан және оны келесі түрде қарастырады. Қирау кернеу кезіндегі серпімді деформация сатысында болады және серпімділік шегі аз.
1. Қирау объектісі болып 2 жағы қатаң бекітілген және туу жарықтары бар бірлік қалыңдықты пластина болып табылады.
2.
Жарықтың пошымы жарты осьті С және 2С
тең эллипс түрінде болады. Жарықтың
көлемі цилиндр көлеміне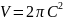 тең.
тең.
Қирау жүретін процесстің бірізділігі:
1.
Серпімді деформация кезінде жарықсыз
пластина көлемінің біріне қалдық
серпімді деформацияға кеткен Гук заңы
бойынша 0-ден σmax
дейінгі өзгеретін аймақтағы кернеу
кезіндегі жұмысқа тең. Бұл жағдайда
орташа әсер ететін кернеу
 ,
ал жұмыс осы өткен жолдағы күштің
шығарылымына тең:
,
ал жұмыс осы өткен жолдағы күштің
шығарылымына тең:
А= ½ σε =½ σ2/Е, (6.1)
мұнда ε = σ/Е.
2. Әсер ететін кернеу бағытына тікбұрыштан орналасқан 2С ұзындығынан денеде жарықтың бірден пайда болуынан эллипсоидалды жарық аймағындағы қалдық серпімді энергияның бөлігі босайды. Ол жарықтардың пропорцианалды көлеміне байланысты. Бұл жағдайда пластинаның серпімді энергиясы W-шамасынан азаяды.
W = ½ σ2/Е 2πc2 = π σ2c2/ Е. (6.2)
-

4с
2с
6.3-сурет. Жүктеудің әртүрлі схемасы. а – еркінжүктеу; б – бекітілген жүктеу
3. Жарықтың туу кезінде меншікті беткейлік энергиясымен 2 жаңа беткейлік түзілуі, бұл 2С-ға тең, жарықтың беткейінің пропорциональды ауданы мен u шамасына пластинасыз ішкі энергияның ұлғаюына әкеледі. Өйткені пластина қалыңдығы 1 деп қабылданады.
U = 4 γs с. (6.3)
4. Жарықтың ауданы 1жағдай кезіндегі қалыңдыққа тең жарықтың 2С ұзындығының шығарымдылығы анықталады. Жарықтың тууы кезіндегі энергетикалық баланс W жарықтану түзілуіне кететін энергия және ішкі беттік энергияның ұлғаюының себебі болатын энергия арасындағы айырмашылыққа тең. Шығын болған энергия теріс, жинақталған энергия оң болып саналады.
ΔU = U – W = 4 γs с - πσ2/Е c2. (6.4)
5. U,W және ∆U арасындағы қатынасқа байланысты баланс оң және теріс болуы тиіс. Егер ∆U=0-ден көп болса, онда жарықтың үлкеюіне энергия қажет. Энергия балансы (-) болады. Егер ∆U=0-оң болса, онда пластинасыз жалпы энергияны жарық пластинаның серпімді энергияның арқасында өздігінен дамиды. Берілген сыртқы кернеу жарықтандыру тұрақсыз өтуге жағдайына σ d∆U- дан dc-ға дейін 0-ге тең болуы кезінде анықталады:
dΔU/ dc = 0 немесе 4 γs - 2πσ2/Е c= 0, (6.5)
демек, σ
=
 . (6.6)
. (6.6)
Алынған теңдеу мортты жарықтың тұрақсыз жайылуының басталуының критикалық жағдайын сипаттайды. Жарықтың ұзындығы қаншалықты ұзын болса, соншылықты кернеу оның жайылуына қажет.

 а
а б
б