
- •Методы оптимизации
- •Вариант № 21
- •Основная идея работы оптимизационных алгоритмов интервальной оценки: дихотомии, золотого сечения, Фибоначчи и др.
- •Связь методов поиска экстремумов и поиска нулей функции.
- •Записать задачу оптимизации общего вида. Что является оптимальным решением задачи оптимизации?
- •Пользуясь любым из методов одномерного поиска, минимизировать функцию с точностью до одного знака после запятой: .
- •Найти минимум целевой функции методом дихотомии на отрезке [1,5;2] с точностью .
- •Свойство параллельного подпространства, геометрическая интерпретация.
- •Прямые методы безусловной многомерной оптимизации: суть симплекс-метода.
- •Минимизировать функцию методом сопряженных направлений, заканчивая вычисления при , где .
- •Провести анализ определенности квадратичной формы:
- •Показать, что точка минимума выпуклой квадратичной функции находится с помощью одной итерации метода Ньютона из произвольного начального приближения.
-
Минимизировать функцию методом сопряженных направлений, заканчивая вычисления при , где .
-
Итерация 1. Шаг 1. Рассмотрим произвольную начальную точку
 и систему линейно независимых направлений
и систему линейно независимых направлений
 и
и
 .
Шаг 2. Минимизируем функцию
.
Шаг 2. Минимизируем функцию
 в направлении
в направлении
 .
Минимум функции
.
Минимум функции
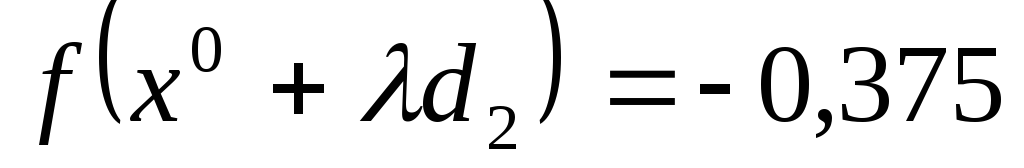 достигается при
достигается при
 в точке
в точке
 .
Минимизируем функцию
.
Минимизируем функцию
 в направлении
в направлении
 .
Минимум функции
.
Минимум функции
 достигается при
достигается при
 в точке
в точке
 .
Минимизируем функцию
.
Минимизируем функцию
 в направлении
в направлении
 .
Минимум функции
.
Минимум функции
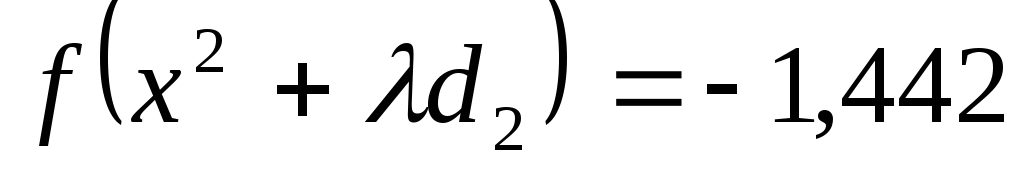 достигается при
достигается при
 в точке
в точке
 .
Шаг 3. Проверим условие
.
Шаг 3. Проверим условие
 .
.
 Шаг
4. Введем новую систему линейно
независимых направлений:
Шаг
4. Введем новую систему линейно
независимых направлений:
 .
Определим сопряженное направление по
теореме о свойстве параллельного
подпространства:
.
Определим сопряженное направление по
теореме о свойстве параллельного
подпространства:

-
Итерация 2. Шаг 1. Продолжим поиск из точки
 .
Шаг 2. Минимизируем функцию
.
Шаг 2. Минимизируем функцию
 в направлении
в направлении
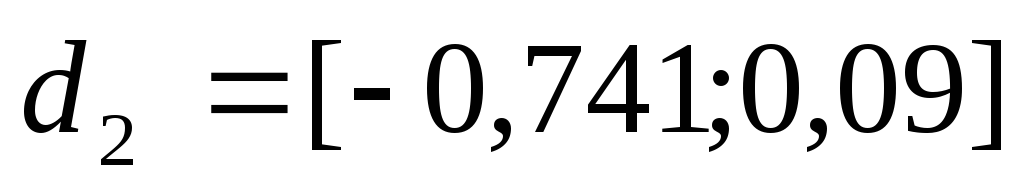 .
Минимум функции
.
Минимум функции
 достигается при
достигается при
 в точке
в точке
 .
Минимизируем функцию
.
Минимизируем функцию
 в направлении
в направлении
 .
Минимум функции
.
Минимум функции
 достигается при
достигается при
 в точке
в точке
 .
Минимизируем функцию
.
Минимизируем функцию
 в направлении
в направлении
 .
Минимум функции
.
Минимум функции
 достигается при
достигается при
 в точке
в точке
 .
Шаг 3. Проверим условие
.
Шаг 3. Проверим условие
 .
.
 Шаг
4. Заданная точность
достигнута.
Шаг
4. Заданная точность
достигнута.
Ответ:
![]() при
при
![]() .
.
-
Провести анализ определенности квадратичной формы:
-
Для положительной определенности квадратичной формы – матрицы А – по критерию Сильвестра необходимо и достаточно, чтобы все угловые миноры матрицы А были положительны.
-
Так как дана квадратичная функция, то матрица А совпадает с матрицей Гессе. Вычислим градиент и матрицу Гессе:

-
Вычислим все угловые миноры матрицы А:

-
Условие положительности, отрицательности, неположительности и неотрицательности всех угловых миноров матрицы А не выполняется и следовательно, данная квадратичная форма не является положительно определенной, отрицательно определенной, отрицательно полуопределенной и положительно полуопределенной.
Ответ: квадратичная
форма
![]() не является положительно и отрицательно
определенной и полуопределенной.
не является положительно и отрицательно
определенной и полуопределенной.
-
Показать, что точка минимума выпуклой квадратичной функции находится с помощью одной итерации метода Ньютона из произвольного начального приближения.
-
Выпуклая квадратичная функция задается уравнением:
 ,
где матрица А положительно определена.
Пусть задана произвольная начальная
точка
,
где матрица А положительно определена.
Пусть задана произвольная начальная
точка
 .
Покажем, что точка минимума данной
целевой функции находится с помощью
одной итерации метода Ньютона из точки
.
Покажем, что точка минимума данной
целевой функции находится с помощью
одной итерации метода Ньютона из точки
 .
. -
Известно, что градиент выпуклой квадратичной функции
 ,
а матрица Гессе
,
а матрица Гессе
 .
Применим итерационную формулу метода
Ньютона:
.
Применим итерационную формулу метода
Ньютона:

-
Убедимся, что найденное решение действительно является точкой минимума и за одну итерацию, было найдено верное решение. Для этого проверим условие стационарности точки:
 (матрица А положительно определена по
условию). Проверяем:
(матрица А положительно определена по
условию). Проверяем:
 ,
что и требовалось показать.
,
что и требовалось показать.
