ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Заочный факультет

(дистанционная форма обучения)

Кафедра автоматизированных систем управления (АСУ)

Методы оптимизации

Текстовая контрольная работа № 1

Вариант № 21

Дата выполнения работы ____________________

Дата проверки _____________________________

Оценка ___________________________________

И.О.Фамилия преподавателя _________________

Подпись преподавателя _____________________

2008 год.

1. Основная идея работы оптимизационных алгоритмов интервальной оценки: дихотомии, золотого сечения, Фибоначчи и др.

• Основная идея работы оптимизационных алгоритмов интервальной оценки сводится к простому сравнению значений функции в двух пробных точках. К методам интервальной оценки (исключения интервалов) относят метод равномерного поиска, метод дихотомии, метод золотого сечения, метод Фибоначчи (предельный случай метода золотого сечения), которые отличаются друг от друга способом выбора этих пробных точек.

2. Связь методов поиска экстремумов и поиска нулей функции.

• Методы поиска нулей функции используются при поиске экстремумов, так как необходимым условием существования локального экстремума (минимума, максимума) функции в некоторой точке является требование стационарности точки , то есть , следовательно, данное уравнение требует поиска нулей функции производной.

3. Записать задачу оптимизации общего вида. Что является оптимальным решением задачи оптимизации?

• Задача оптимизации общего вида с ограничениями в пространстве :

• Задача: минимизировать целевую функцию с ограничениями (при множестве условий) и найти при этом решение задачи - вектор .

• Оптимальным решением задачи оптимизации общего вида (глобальным экстремумом) называют такой вектор , минимизирующий значение на множестве всех решений: для всех .

4. Пользуясь любым из методов одномерного поиска, минимизировать функцию с точностью до одного знака после запятой: .

• Используем метод средней точки (поиск Больцано). Первая цифра после запятой будет верной в узком смысле, если погрешность . Определим .

• Итерация 1. Шаг 1. Положим R=4; L=0, при этом . Шаг 2. Вычислим . Шаг 3. , положим R=2, так как .

• Итерация 2. Шаг 2. Вычислим . Шаг 3. , положим R=1, так как .

• Итерация 3. Шаг 2. Вычислим . Шаг 3. , положим R=0,5, так как .

• Итерация 4. Шаг 2. Вычислим . Шаг 3. , положим L=0,25, так как .

• Итерация 5. Шаг 2. Вычислим . Шаг 3. , положим L=0,375, так как .

• Итерация 6. Шаг 2. Вычислим . Шаг 3. , точность достигнута.

• .

Ответ:

5. Найти минимум целевой функции методом дихотомии на отрезке [1,5;2] с точностью .

• Пусть . Построим последовательность вложенных отрезков по рекуррентным формулам и занесем результаты в таблицу.

  									Примечание
  0	1,5	2	1,75	1,74	1,76	-92,13505	-92,09627	0,71875>0,5 Критерий останова не выполняется
  1	1,5	1,75	1,625	1,615	1,635	-91,42825	-91,64744	|-1,3418|>0,5 Критерий останова не выполняется
  2	1,625	1,75	1,688	1,678	1,698	-91,98429	-92,07692	|-0,2892|<0,5

• Останов: 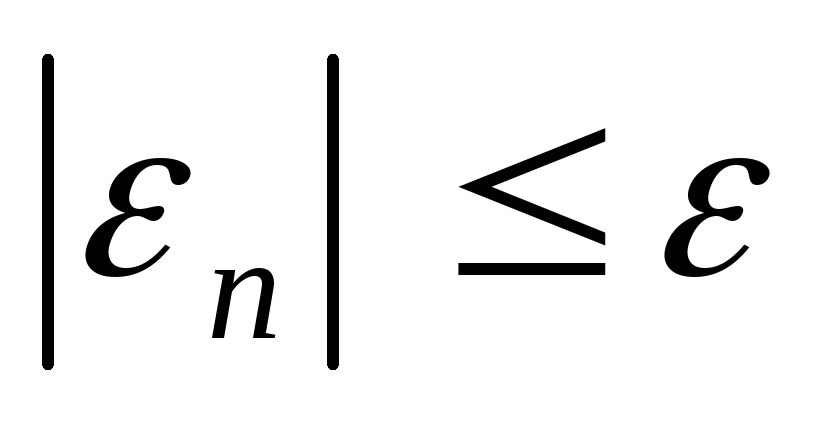, здесь: 0,2892<0,5. Следовательно, и

Ответ: .