6. Метод линеаризации для задачи нелинейного программирования общего вида.

• Рассмотрим общую задачу нелинейного программирования:

• Линеаризация этой задачи по сути сводит все к решению задачи с линейными ограничениями. Использование линеаризации дает возможность применять методы линейного программирования.

• Методы линеаризации основываются на разложении нелинейной функции общего вида в ряд Тейлора до членов первого порядка в окрестности некоторой точки : 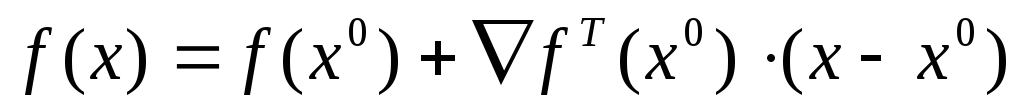. Таким образом, функция 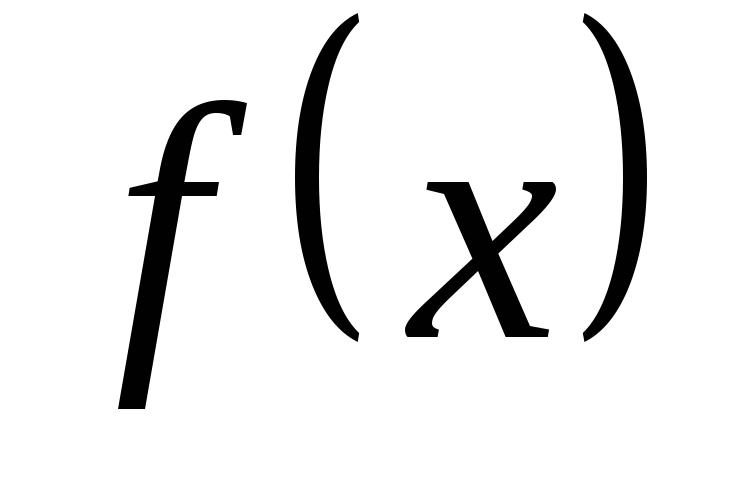аппроксимируется в точке линейной функцией: .

• Пусть - некоторая заданная оценка решения. Используя линеаризацию для общей задачи нелинейного программирования, получим: - задачу линейного программирования.

• Для сходимости данной задачи к истинному экстремуму достаточно, чтобы для последовательности точек , полученных в результате решения подзадач линейного программирования, выполнялось следующее условие: значение целевой функции и невязки по ограничениям в точке должно быть меньше их значений в точке .

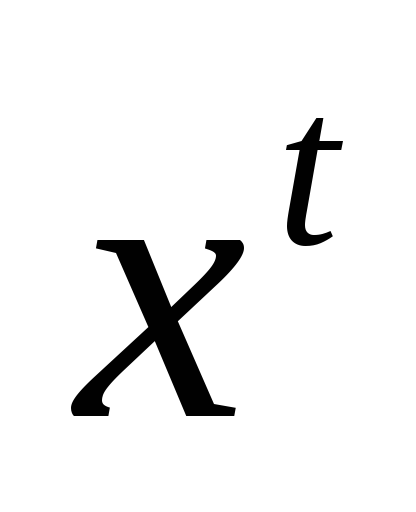7. Условная оптимизация. Метод множителей Лагранжа. Пример.

• Условная оптимизация целевой функции подразумевает решение задачи оптимизации целевой функции с ограничениями. Метод множителей Лагранжа позволяет найти экстремум в задаче оптимизации с ограничениями-равенствами. При этом сама задача с ограничениями преобразуется в эквивалентную задачу безусловной оптимизации, в которой используются параметры – множители Лагранжа.

• Рассмотрим задачу линейной оптимизации с ограничениями-равенствами: , где . По методу Лагранжа эта задача преобразуется в задачу безусловной оптимизации: , где функция - функция Лагранжа, - множитель Лагранжа, любого знака.

• Рассмотрим пример. Пусть . Соответствующая задача оптимизации без ограничений выглядит так: Найдем стационарную точку: Проверим, соответствует ли стационарная точка минимуму, для этого вычислим матрицу Гессе функции , рассматриваемой как функция от х: , которая оказывается положительно определенной, тогда функция является выпуклой. Следовательно, точка 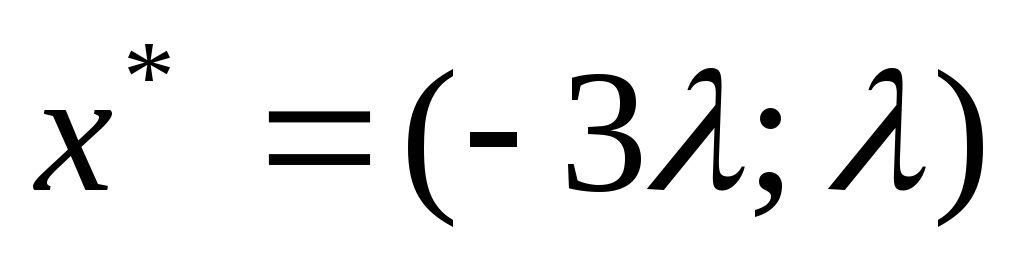- точка глобального минимума. Оптимальное значение определяется подстановкой значений и в уравнение ограничений: , откуда вычисляем : .

Тогда минимум достигается в точке , .

8. Двойственная функция для задачи линейного программирования.

• Рассмотрим задачу линейного программирования: при ограничениях . Эту задачу называют прямой. Существует связанная с ней задача максимизации, называемая двойственной задачей: при ограничениях

• Функция называется функцией Лагранжа или двойственной функцией задачи линейного программирования.

9. Найти экстремум целевой функции: при условии . Привести графическую иллюстрацию решения. Предложить не менее трех подходов к решению данной задачи оптимизации.

• Рассмотрим графическое решение данной задачи с двумя переменными. Изобразим множество точек на плоскости, удовлетворяющих ограничению , которое равносильно условию: . Все точки этой прямой входят в область допустимых решений ОДР данной задачи.

• Если зафиксировать положительное значение функции , то соответствующие ему точки будут лежать на некоторой окружности с центром в начале координат. При изменении этого значения функции радиус окружности будет уменьшаться или увеличиваться. Рассмотрим концентрические окружности, соответствующие различным значениям целевой функции, имеющие с ОДР хотя бы одну общую точку. Возможны три случая: окружность не имеет общих точек с прямой ОДР (при ), имеет ровно одну общую точку (при ), имеет ровно две общие точки (при ). При уменьшении радиуса окружности значение целевой функции уменьшается, таким образом наименьшее значение целевой функции достигается на ОДР при касании окружности и прямой ОДР, то есть при . Тогда - оптимальное значение целевой функции при оптимальном решении . Ответ: .

• Решим эту же задачу методом замены переменных: выразим из уравнения ограничения переменную через и получим 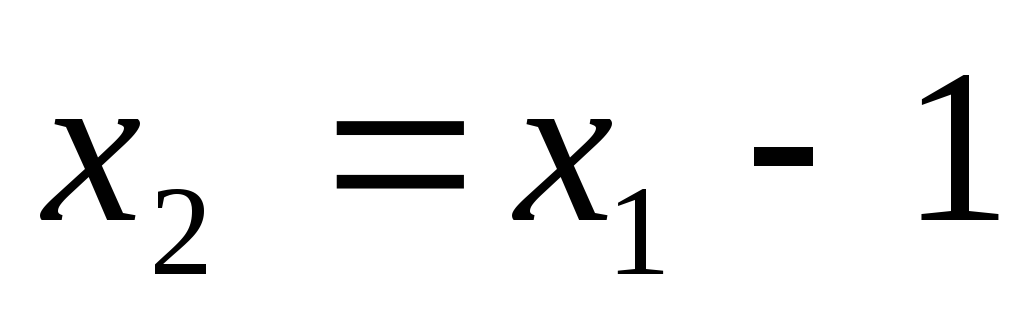, подставим в целевую функцию. Тогда .

Ответ: .

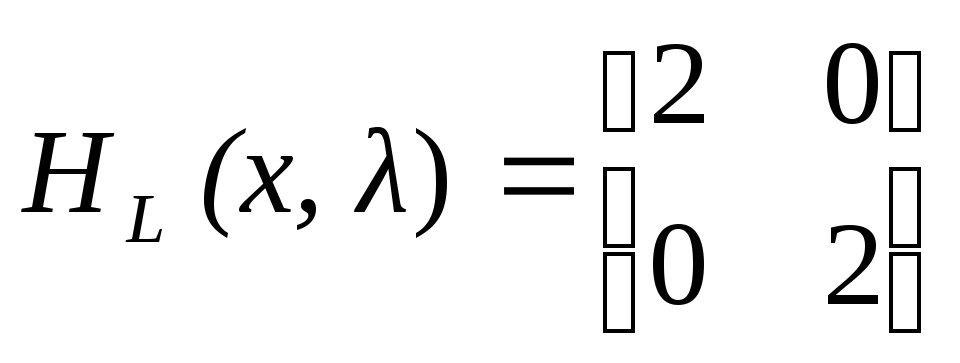• Решим эту же задачу методом множителей Лагранжа: . Соответствующая задача оптимизации без ограничений записывается в следующем виде: . Вычислим:Для того, чтобы проверить, соответствует ли стационарная точка минимуму, вычислим матрицу Гессе функции , рассматриваемой как функция от х: , которая оказывается положительно определенной. Это означает, что выпуклая функция. Следовательно, координаты определяют точку глобального минимума. Оптимальное значение определяется подстановкой значений и в уравнение ограничений: , откуда вычисляем : . Тогда минимум достигается в точке , . Ответ: .

• Решим эту же задачу оптимизации методом штрафных функций (квадратичный штраф). Введем штрафную функцию вида: . Запишем уравнения, определяющие стационарную точку штрафной функции: 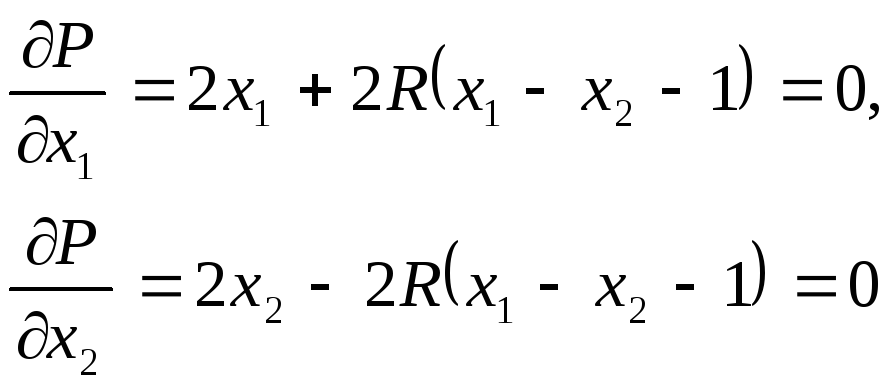, откуда следует: . Переходя к пределу, получим: . Таким образом, метод сходится к точке и . В таблице приведены координаты стационарных точек штрафной функции:

0	0	0	0
0,1	0,08333333	0,08333333	0,01388889
1	0,33333333	0,33333333	0,22222222
10	0,47619048	0,47619048	0,45351474
100	0,49751244	0,49751244	0,49503725
∞	0,5	0,5	0,5

Ответ:

Данная задача оптимизации решена 4 методами: графическим, замены переменной, множителей Лагранжа, штрафных функций. Все 4 метода дали одинаковый ответ: .

10. В состав автопилота (АП) летательного аппарата входят гироскоп (Г) и бортовой компьютер (БК). Их энергетические параметры составляют: Г- условных единиц (у.е.); БК- у.е. Масса АП равна:. Критерий точности работы АП: . Найти параметры АП, максимизирующие точность его работы, при условии того, что масса АП не превышает 16 у.е., т.е. . Задачу решить методом множителей Лагранжа.

• Функция по условию задачи определена на множестве: . Максимальную точность обеспечивает минимальное значение погрешности. Сформулируем данную задачу нелинейного программирования в общем виде: . Заметим, что метод множителей Лагранжа применяется для задач с ограничениями-равенствами, что в данном случае нарушено. Но известно, что подход Лагранжа усовершенствован и обобщен в методе Куна-Таккера для задач со смешанными ограничениями. Воспользуемся этим усовершенствованным методом множителей Лагранжа.

• Преобразуем данную задачу к стандартному виду:

• Функция выпукла на своей области определения, так как матрица Гессе имеет вид: и положительно определена при .

• Запишем условия Куна-Таккера для данной задачи:

• Из этих условий находим: . Мы нашли точку , которая может быть точкой минимума. Для этой точки ограничение , то есть активно. Проверим следующее условие. 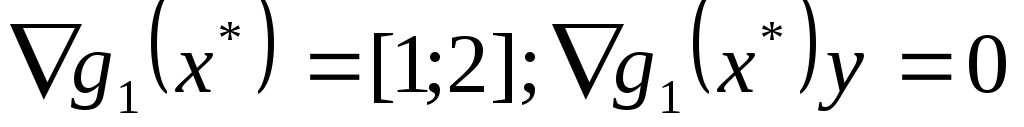будет верно для всех векторов вида . Матрица Гессе функции L в точке имеет вид: . Матрица Гессе положительно определена и, следовательно, неравенство выполняется для любого ненулевого вектора, в том числе для вектора . Также положительно полуопределена матрица , следовательно функция-ограничение является выпуклой (необходимое условие для ). Все условия Куна-Таккера выполнены. Тогда точка является точкой строгого локального минимума.

• Получим: условие максимизации точности АП выполняется при наибольшей массе АП , при энергетических параметрах гироскопа 8 у.е., бортового компьютера 4 у.е. и составляет точность: .

Ответ: .