-
Решить транспортную задачу методом наименьшей стоимости. При одновременном выполнении ограничений всегда вычеркивать строку.
Пункты назначения
Объем производства
1
2
3
4
Исходные пункты
1
10
2
20
11
15
2
12
7
9
20
25
3
0
14
16
18
5
Спрос
5
15
15
10
-
Начнем процедуру с переменной
,
которой соответствует минимальная
стоимость
.
Вычеркиваем строку 3:Пункты назначения
Объем производства
1
2
3
4
Исходные пункты
1
10
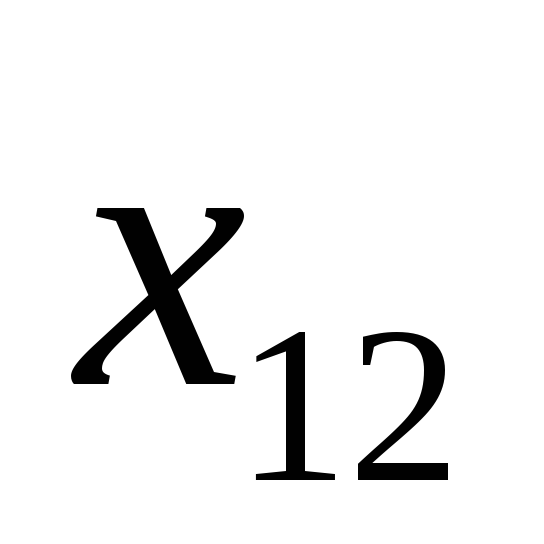
2
20
11
15
2
12
7
9
20
25
3
5
0
×
14
×
16
×
18
5
Спрос
5
Остается 5-5=0 единиц
15
15
10
-
Наименьший невычеркнутый элемент
.Вычеркиваем
строку 1:Пункты назначения
Объем производства
1
2
3
4
Исходные пункты
1
×
10
15
2
×
20
×
11
15
2
12
7
9
20
25
3
5
0
×
14
×
16
×
18
5
Спрос
5
Остается 5-5=0 единиц
15
Остается 15-15=0 единиц
15
10
-
Наименьший невычеркнутый элемент
.
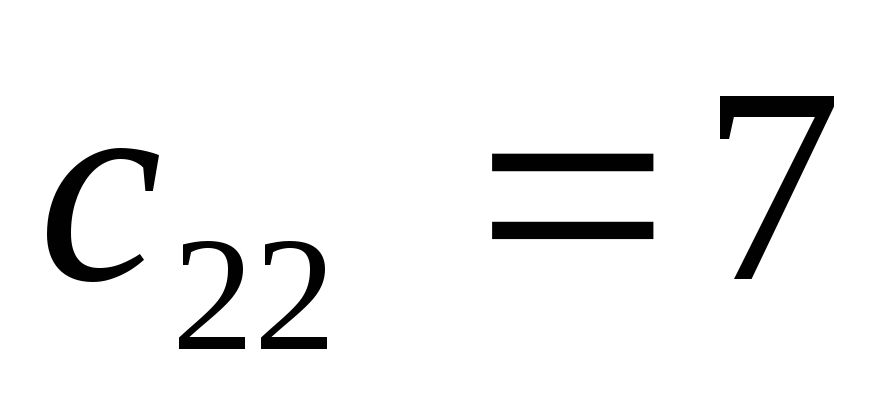Вычеркиваем столбец 2:Пункты назначения
Объем производства
1
2
3
4
Исходные пункты
1
×
10
15
2
×
20
×
11
15
2
12
0
7
9
20
25
Остается 25-0=25 единиц
3
5
0
×
14
×
16
×
18
5
Спрос
5
Остается 5-5=0 единиц
15
Остается 15-15=0 единиц
15
10
-
Наименьший невычеркнутый элемент
.
Вычеркиваем столбец 3:Пункты назначения
Объем производства
1
2
3
4
Исходные пункты
1
×
10
15
2
×
20
×
11
15
2
12
0
7
15
9
20
25
Остается 25-15=10 единиц
3
5
0
×
14
×
16
×
18
5
Спрос
5
Остается 5-5=0 единиц
15
Остается 15-15=0 единиц
15
10
-
Наименьший невычеркнутый элемент
.
Вычеркиваем столбец 1:Пункты назначения
Объем производства
1
2
3
4
Исходные пункты
1
×
10
15
2
×
20
×
11
15
2
0
12
0
7
15
9
20
25
Остается 10-0=10 единиц
3
5
0
×
14
×
16
×
18
5
Спрос
5
Остается 5-5=0 единиц
15
Остается 15-15=0 единиц
15
10
-
Получаем:
:Пункты назначения
Объем производства
1
2
3
4
Исходные пункты
1
×
10
15
2
×
20
×
11
15
2
0
12
0
7
15
9
10
20
25
3
5
0
×
14
×
16
×
18
5
Спрос
5
15
15
10
-
Получим следующее базисное решение по методу наименьшей стоимости:
. -
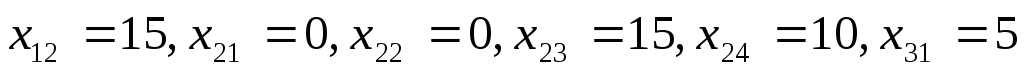Суммарные затраты, соответствующие этому базисному решению, равны:
.
Ответ:
наименьшая сумма затрат данной
транспортной задачи равна 365 при базисном
решении
,
,
,
.