ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Заочный факультет
(дистанционная форма обучения)
Кафедра автоматизированных систем управления (АСУ)
Методы оптимизации
Текстовая контрольная работа № 2
Вариант № 21
Дата выполнения работы ____________________
Дата проверки _____________________________
Оценка ___________________________________
И.О.Фамилия преподавателя _________________
Подпись преподавателя _____________________
2008 год.
-
Основное неравенство теории двойственности.
-
Рассмотрим задачу линейного программирования в стандартной форме:
- прямая задача. -
Каждому i-тому ограничению поставим в соответствие переменную
,
называемую двойственной переменной. -
Рассмотрим двойственную задачу линейного программирования:
- двойственная задача, где U
– вектор-строка. -
Основное неравенство теории двойственности сформулировано в следующей теореме.
-
Теорема двойственности. Если X и U – соответственно допустимые решения произвольной прямой и двойственной задач, то
. -
Это неравенство имеет важное для решения задач линейной оптимизации следствие: Если
и
-
соответственно решения прямой и
двойственной задач, удовлетворяющие
равенству:
,
то планы
и
- оптимальные решения прямой и
двойственной задач соответственно.
-
Понятие базисного и допустимого базисного решения задачи линейного программирования.
-
Рассмотрим общую задачу линейного программирования с m ограничениями и n переменными, записанную в стандартной (канонической) форме:
-
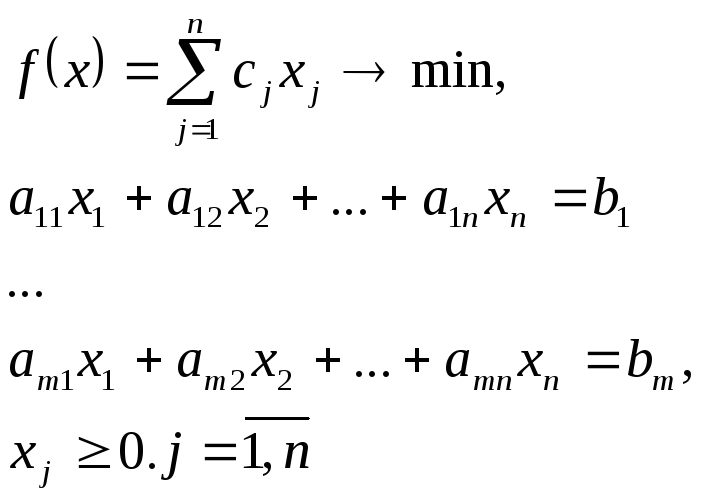
При классическом решении системы линейных уравнений методом Гаусса-Жордана данная система ограничений приобретает вид:
-
Переменные
,
входящие с единичным коэффициентом
только в одно уравнение полученной
системы, а в остальные уравнения с
нулевым коэффициентом, называются
базисными или зависимыми переменными.
Остальные n-m переменных
(
)
называются небазисными или независимыми
переменными. -
Определение. Базисным решением системы ограничений, преобразованной по методу Гаусса-Жордана, называется решение, полученное при нулевых значениях небазисных переменных.
-
Определение. Базисное решение называется допустимым, если значения входящих в него базисных переменных неотрицательны, что эквивалентно условию
. -
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется также опорным планом.
Преобразовать
задачу линейного программирования к
стандартной форме:
и
переменная
не
ограничена по знаку.
-
Шаг 1. Заменим
на
,
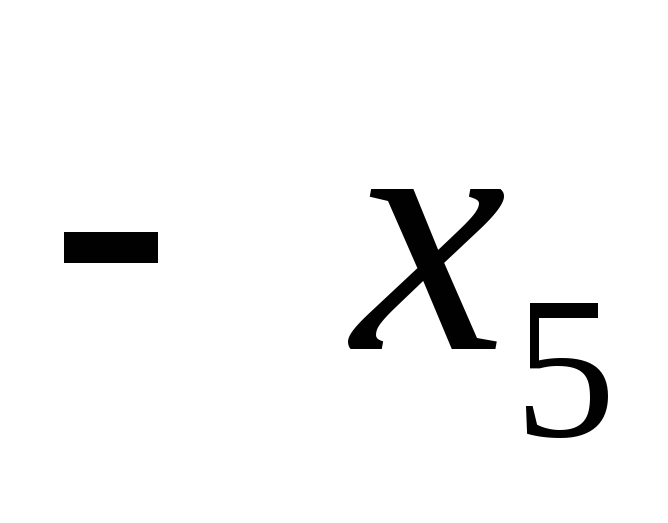где
. -
Шаг 2. Заменим
на
,
где
. -
Шаг 3. Умножим обе части уравнения (1) на (-1).
-
Шаг 4. Введем дополнительные переменные
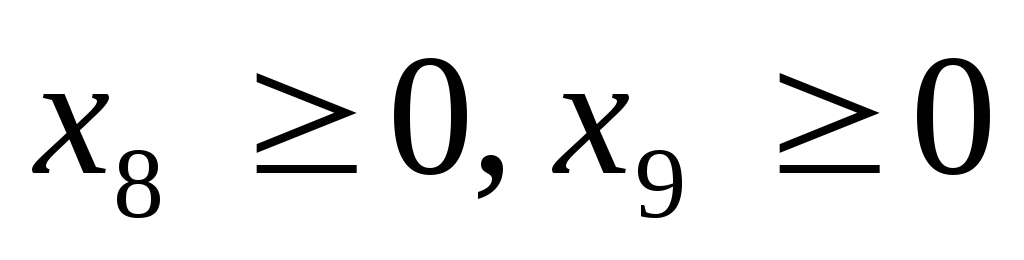в ограничения (2) и (3) соответственно. -
Шаг 5. Припишем нулевой коэффициент переменным
,
а целевую функцию умножим на (-1). -
Тогда рассматриваемая задача сводится к следующей задаче линейного программирования в стандартной форме:
Ответ:
