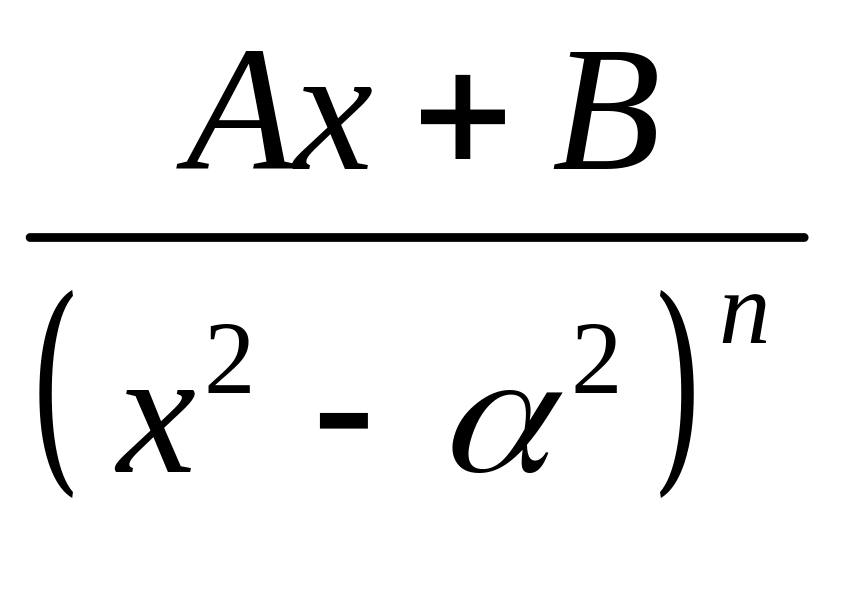Тест / mt22 (жавобли, 2-семестр учун) РУС
.docМатематический анализ: тесты (I курс бакалавриат, II семестр)
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
3. Какое из следующих равенств неверно? |
* |
|
|
|
|
4. Какое из следующих равенств неверно? |
* |
|
|
|
|
5. При вычислении интеграла
|
* 3 шт; |
2 шт; |
1 шт; |
4 шт. |
|
6. При каком случае интеграл
|
*
|
|
|
|
|
7. Какой ответ правильный?
Функция
|
* она неограничена на отрезке [a, b]; |
она возрастает и ограничена на отрезке [a, b]; |
она непрерывна на отрезке [a, b]; |
она убывает и ограничена на отрезке [a, b], |
|
8. Какие функции интегрируются всегда?1) непрерывные на [a, b]; 2) монотонные и ограниченые на [a, b]; 3) произвольные и ограниченные на [a, b]; 4) произвольные функции, заданные на [a, b]: |
* 1) и 2); |
3); |
4); |
3) и 4). |
|
9. Какие из следующих равенств неправильны? |
* |
|
|
|
|
10. Какое из следующих равенств неправильно? |
* |
|
|
|
|
11.
|
* |
|
|
|
|
12.
|
* |
|
|
|
|
13.
|
* |
|
|
|
|
14.
|
* |
|
|
|
|
15.
|
* |
|
|
|
|
16.
|
|
|
* |
|
|
17.
|
* |
|
|
|
|
18.
|
* |
|
|
|
|
19.
|
* |
|
|
|
|
20.
|
* |
|
|
|
|
21. Какая из следующих формул не выражает площадь плоской фигуры? |
* |
|
|
|
|
22. Какая из следующих формул выражает площадь поверхности вращения? |
* |
|
|
|
|
|
|
|
|
|
|
||
23. Какая из следующих формул не выражает длину дуги плоской кривой? |
* |
|
|
|
|
||
24. Какая из следующих формул выражает объема тела вращения? |
* |
|
|
|
|
||
25. Укажите гармонический ряд: |
* |
|
|
|
|
||
26. Какой из пределов надо вычислить, чтобы применить радикальный признак Коши? |
* |
|
|
|
|
||
27. Какой из пределов надо вычислить, чтобы применить признака Даламбера? |
* |
|
|
|
|
||
28. Какой из пределов надо вычислить, чтобы применить интегральный признак Коши? |
* |
|
|
|
|
||
29. Какой из пределов надо вычислить, чтобы применить признака Раабе? |
* |
|
|
|
|
||
30. Укажите необходимое условие
сходимости ряда (здесь
|
* |
|
|
|
|
||
31. Пусть выполняется
хотя бы одно из следующих условий для
функционального ряда
|
* 1) и 3); |
2); |
1) и 2); |
1). |
|
||
32. Пусть выполняется
хотя бы одно из следующих условий для
функционального ряда
:
1) каждый член
ряда
непрерывен на множестве М
; 2) ряд
сходится на множестве М;
3) ряд
сходится равномерно на множестве М.
При выполнении какие из этих условий
верна следующая теорема?(здесь М
– отрезок [a, b]).
Можно интегрировать ряд
почленно по отрезку [a,
b] и имеет место
равенство
|
* 1) и 3); |
1); |
2); |
1) и 2). |
|
||
33. Пусть выполняется
хотя бы одно из следующих условий для
функционального ряда
:
1) каждый член
ряда
имеет конечный предел
|
* 1) и 3); |
1); |
1) и 2); |
этот ряд произвольно. |
|
||
34. Пусть выполняется
хотя бы одно из следующих условий для
функционального ряда
:
1) каждый член
ряда
имеет на отрезке
|
*1), 2), 4); |
1), 2); |
1); |
1), 2), 3). |
|
||
35. Теорема Абеля. Если
ряд
|
* для всех значений
,
удовлетворяющих неравенству
|
для всех значений
,
удовлетворяющих неравенству
|
для всех значений сходится; |
Расходится для всех
значений
,
за исключением
|
|
||
36. При выборе какой из
ответов не имеет место следующая
теорема?Если функция
|
*не интегрируема на этом множестве; |
достигает своей точной верхней и точной нижней грани на этом множестве; |
ограничена на этом множестве; |
равномерно непрерывна на этом множестве. |
|
||
37. Найти площадь фигуры,
ограниченной линиями, уравнениями
которых имеют вид
|
* |
|
|
|
|
||
38. Найти площадь фигуры, ограниченной
параболами
|
* |
|
|
|
|
||
39. Найти площадь
фигуры, ограниченной параболами
и
|
* |
|
|
|
|
||
40. Найти площадь
фигуры, ограниченной параболами
|
* |
|
|
|
|
||
41. Сколько теорем сравнения положительных рядов имеются? |
*3 шт. |
2 шт |
1 шт |
4 шт |
|
||
42. Пусть заданы ряды
|
*при сходимости ряда сходится и ряд . |
при сходимости ряда сходится и ряд . |
при расходимости ряда расходится и ряда . |
выполняется или . |
|
||
43. Пусть заданы ряды и . При выполнении какое из условий верно утверждение: Если начиная с некоторого значения имеет место неравенство , то |
* при расходимости ряда расходится и ряда . |
при расходимости ряда расходится и ряда . |
при сходимости ряда сходится и ряд . |
выполняется или . |
|
||
44. Пусть заданы ряды
и
.
При выполнении какое из условий верно
утверждение: Если начиная с некоторого
значения
имеет место неравенство
|
*при сходимости ряда сходится и ряд . |
при расходимости ряда расходится и ряда . |
выполняется или . |
при сходимости ряда сходится и ряд . |
|
||
45. Пусть заданы ряды и . При выполнении какое из условий верно утверждение: Если начиная с некоторого значения имеет место неравенство , то |
* при расходимости ряда расходится и ряда . |
при расходимости ряда расходится и ряда . |
при сходимости ряда сходится и ряд . |
выполняется или . |
|
||
46. Пусть
заданы ряды
и
и существует предел
|
*при сходимости ряда сходится и ряд . |
при сходимости ряда
расходится ряд
|
выполняется или . |
при сходимости ряда сходится и ряд . |
|
||
47. Пусть
заданы ряды
и
и существует предел
.
При выполнении какое из условий верно
утверждение : если
|
* при расходимости ряда расходится и ряда . |
при сходимости ряда сходится и ряд . |
при сходимости ряда расходится ряд . |
выполняется или . |
|
||
48. Пусть
заданы ряды
и
и существует предел
.
При выполнении какое из условий верно
утверждение: если
|
*ряды
и
|
при сходимости ряда расходится ряд . |
при сходимости ряда расходится ряд . |
выполняется или . |
|
||
49. Найти длину цепной
линии
|
* |
|
|
|
|
||
50. Найти длину дуги кривой
|
* |
|
|
|
|
||
51. Ряд
|
* |
|
|
|
|
||
52. Ряд
|
* |
|
|
|
|
||
53. Ряд
|
* |
|
|
|
|
||
54. Фигура, ограниченная
параболами
и
|
*
|
|
|
|
|
||
55. Ряд
|
*
|
|
|
|
|
|
|
56. Ряд
|
* |
|
|
|
|
||
57. Если функция
является четной функцией на
|
* |
|
|
|
|
||
58. Если функция является нечетной функцией на , то укажите ряд Фурье этой функции. |
* |
|
|
|
|
||
59. Найти площадь поверхности
вращения, полученной при вращении
астроиды
|
* |
|
|
|
|
||
60. Найти сумму ряда
|
*
|
|
|
|
|
||
61. Найти
сумму ряда
|
* |
|
|
|
|
||
62. Найти
сумму ряда
|
* |
|
|
|
|
||
63. Найти сумму ряда
|
* |
|
|
|
|
||
64. Найти
сумму ряда
|
* |
|
|
|
|
||
65. Найти
сумму ряда
|
* |
|
|
|
|
||
66. Найти сумму ряда
|
* |
|
|
|
|
||
67. Найти сумму ряда
|
* |
|
|
|
|
||
68. Найти сумму ряда
|
* |
|
|
|
|
||
69. Найти сумму ряда
|
*
|
|
|
|
|
||
70. Какой из рядов 1) |
* 3); |
2); |
1); |
1) и 2). |
|
||
71. Какой
из рядов 1) |
* 2); |
1); |
3); |
1) и 3). |
|
||
72. Какой из рядов 1) |
* 1); |
2); |
2) и 3); |
3). |
|
||
73. Какой из рядов 1) |
* 3). |
2); |
1) и 2); |
1); |
|
||
74. Какой из рядов
1)
|
* все; |
1) и 3); |
2) и 3); |
1) и 2). |
|
||
75. Какой
из рядов 1)
|
* 2); |
1); |
3); |
1) и 3). |
|
||
76. Какой из рядов 1)
|
* 2) и 3); |
1) и 2); |
1); |
все. |
|
||
77. Какой
из рядов 1)
|
* 2) и 3); |
1); |
1) и 3); |
все. |
|
||
78. Какой
из рядов 1)
|
* 1); |
2); |
3); |
2) и 3). |
|
||
79. Какой
из рядов 1)
|
* 1) и 3); |
1) и 2); |
2); |
все. |
|
||
80. Какой из рядов
1)
|
* 1); |
2); |
3); |
2) и 3). |
|
||
81. Какой из рядов
|
* 1) и 3); |
1) и 2); |
2); |
2) и 3). |
|
||
82. Какой из рядов
1)
|
* 3); |
2); |
1); |
1) и 2). |
|
||
83. Найти область сходимости ряда
|
* |
|
|
|
|
||
84. Найти область
сходимости ряда
|
* |
|
|
|
|
||
85. Найти область сходимости ряда
|
* |
|
|
|
|
||
86. Найти область сходимости ряда
|
* |
|
|
|
|
||
87. Найти область сходимости ряда
|
* |
|
|
|
|
||
88. Найти область сходимости ряда
|
* |
|
|
|
|
||
89. Найти область сходимости ряда
|
*
|
|
|
|
|
||
90. Найти область сходимости ряда
|
* |
|
|
|
|
||
91. Ряд
|
* |
|
|
|
|
||
92. Ряд
|
* |
|
|
|
|
||
93. Найти область сходимости ряда
|
*
|
|
|
|
|
||
94. Найти область сходимости ряда
|
* |
|
|
|
|
||
95. Найти область
сходимости ряда
|
* |
|
|
|
|
||
96. Найти область сходимости ряда
|
* |
|
|
|
|
||
97. Найти область сходимости ряда
|
* |
|
|
|
|
||
98. Найти область сходимости ряда
|
* |
|
|
|
|
||
99. Найти область сходимости ряда
|
* |
|
|
|
|
||
100. Найти область
сходимости ряда
|
*
|
|
|
. |
|
||
101. Найти область сходимости ряда
|
* |
|
|
|
|
||
102. Найти область сходимости ряда
|
*
|
|
|
|
|
||
103. |
|
|
|
|
|
||
104. Разложить функцию
|
|
|
|
|
|
||
105. Найти точки перегиба функции
|
|
|
|
ва
|
|
||
106. Найти интервалы выпуклости и вогнутости функции . |
в
|
в выпукла, а в вогнута |
|
в вогнута, а в выпукла |
|
||
107. |
|
|
|
|
|
||
108. |
|
|
|
|
|
||
109. Найти площадь фигуры,
ограниченной линиями
|
|
|
|
|
|
||
110. Укажите формулу интегрирования по частям в определенном интеграле. |
|
|
|
|
|
||
111. |
|
|
|
|
|
||
112. Найти объем тела
вращения криволинейной трапеции
|
|
|
|
|
|
||
113. Найти длину дуги части
кривой
|
|
6 |
|
7 |
|
||
114. |
|
|
|
|
|
||
115. Если функция
непрерывна на отрезке
|
|
|
|
|
|
||
116. |
2 |
|
1 |
0 |
|
||
117. |
|
|
|
|
|
||
118. |
|
|
|
|
|
||
119. |
|
|
|
|
|
||
120. |
|
|
|
|
|
||
121. |
|
|
|
|
|
||
122. |
|
|
|
|
|
||
123. Найти длину дуги кривой
|
|
|
|
|
|
||
124. |
|
|
|
|
|
||
125. |
|
0 |
|
|
|
||
126. |
|
|
|
|
|
||
127. |
|
|
|
|
|
||
128. |
|
|
|
|
|
||
129. |
|
|
|
|
|
||
130. |
|
|
|
|
|
||
131. |
|
|
|
|
|
||
132. |
|
|
|
|
|
||
133. |
|
|
|
|
|
||
134. |
|
|
|
|
|
||
135. Вычислить площадь кардиоиды
|
|
|
|
|
|
||
136. |
|
|
|
|
|
||
137. |
|
|
|
|
|
||
138. |
|
|
|
|
|
||
139. Функция
|
|
|
|
|
|
||
140. Разложить
|
|
|
|
|
|
||
141. |
|
|
|
|
|
||
142. |
|
|
|
|
|
||
143. |
|
|
|
|
|
||
144. Укажите радикальный признак Коши для положительного ряда. |
|
|
|
|
|
||
145. Укажите признак Даламбера для положительного ряда. |
|
|
|
|
|
||
146. При каких значениях
|
|
|
|
|
|
||
147. Если ряд
|
Для
|
Для расходится. |
Для
|
Для
|
|
||
148. |
|
|
|
|
|
||
149. Пусть функции
|
|
|
|
Для произвольных |
|
||
150. |
|
|
|
|
|
||
151. |
|
|
|
|
|
||
152. Найти суммы ряда
|
|
|
|
|
|
||
153. Какой из нижеследующих рядов сходится? |
|
|
|
|
|
||
154. |
|
0 |
|
|
|
||
155. |
|
|
0 |
|
|
||
156. Укажите необходимое и достаточное условия сходимости произвольного ряда. |
Для
|
Для
существует
такое, что для
выполняется неравенство
|
Для
существует
такое, что для
и
выполняется неравенство
|
Для
существует
такое, что для
выполняется неравенство
|
|
||
157. Укажите сходящегося из нижеследующих рядов. |
|
|
|
|
|
||
158. Укажите сходящегося из нижеследующих рядов. |
|
|
|
|
|
||
159. Укажите сходящегося из нижеследующих рядов. |
|
|
|
|
|
||
160. |
|
|
|
|
|
||
161. Укажите расходящегося из нижеследующих рядов. |
|
|
|
|
|
||
162. Укажите сходящиеся из нижеследующих рядов. |
|
|
|
,
|
|
||
163. При выполнении каких
из условий следует теорема Лейбница,
выражающая сходимость знакочередующихся
рядов? 1) |
1), 2); |
2), 3); |
1), 4); |
3), 4). |
|
||
164. Найти сумму ряда
|
|
|
|
|
|
||
165. Если ряд
|
Сходится абсолютно |
Сходится условно |
Расходится |
Может быть как сходящимся так и расходящимся. |
|
||
166. Для сходимости положительных рядов какое из условий является необходимым и достаточным условием? |
Для сходимости положительных рядов необходимо и достаточно, чтобы была ограничена последовательность частичных сумм. |
Для сходимости положительных рядов необходимо и достаточно, чтобы была ограничена последовательность частичных сумм снизу. |
Для сходимости положительных рядов необходимо и достаточно, чтобы была монотонна последовательность частичных сумм. |
Для сходимости положительных рядов необходимо и достаточно, чтобы не была монотонна последовательность частичных сумм. |
|
||
167. Найти
|
|
|
|
|
|
||
168. Какой из следующих рядов сходится абсолютно? |
|
|
|
|
|
||
169. Какие из следующих дробей являются
простыми дробями? 1)
|
1), 2) |
1), 3) |
3), 4) |
1), 4) |
|
||
170. Какие из следующих
дробей являются простыми дробями?
1)
|
1), 3) |
1), 2) |
2), 4) |
3), 4) |
|
||
171. Укажите нижнюю сумму
Дарбу:1) |
1) |
2) |
3) |
4) |
|
||
172. Укажите верхнюю сумму Дарбу:1) ; 2) ; 3) ;4) , бунда , , . |
2) |
1) |
3) |
4) |
|
||
173. Укажите интегральную сумму:1) ; 2) ; 3) ;4) , бунда , , . |
3) |
1) |
2) |
4) |
|
||
174. Для существования
определенного интеграла необходимо
и достаточно, чтобы был равен нулю
предел какой из нижеследующих сумм
при
|
4) |
2) |
1) |
3) |
|
||
175. Сколько свойств имеют сумм Дарбу? |
2 та |
1 та |
3 та |
4 та |
|
||
176. Какая из теорем не имеет место? |
Если функция
|
Если функция непрерывна на отрезке , то она интегрируема на этом отрезке. |
Если функция монотонна и ограничена на отрезке , то она интегрируема на этом отрезке. |
Если функция ограничена на отрезке и имеет разрыв в конечных точках этого отрезка, а в остальных точках непрерывна, то она интегрируема на этом отрезке. |
|
||
177. Найти вид числового ряда. |
|
|
|
|
|
||
178. Найти коэффциент
|
0 |
|
|
1 |
|
||
179. Найти коэффциент
|
0 |
1 |
|
|
|
||
180. Найти коэффциент
ряда Фурье функции
|
0 |
|
|
1 |
|
||
181. Укажите периодические функции. |
|
|
|
|
|
||
182. Найти сумму ряда |
|
|
|
|
|
||
183. Найти область сходимости
функционального ряда
|
|
|
|
|
|
||
184. Найти область
сходимости функционального ряда
|
|
|
|
|
|
||
185. Найти область
сходимости функционального ряда
|
|
|
|
|
|
||
186. Найти разложение
функции
|
|
|
|
|
|
||
187. Ряд
|
|
|
|
|
|
||
188. Ряд
|
|
|
|
|
|
||
189. Дайте определение на сумму числового ряра? |
Суммой числового ряда
называется предел
члена последовательности
частичных сумм при
|
Суммой числового ряда называется предел общего члена при |
Суммой числового ряда называется сумму первых членов ряда |
Абсолютное значение членов данного ряда |
|
||
190. Найти радиус сходимости
ряда
|
|
0 |
1 |
2 |
|
||
191. Найти интервал сходимости ряда . |
|
Сходится только в точке 0 |
|
|
|
||
192. Найти радиус сходимости
ряда
|
2 |
3 |
1 |
4 |
|
||
193. Найти интервал сходимости ряда . |
|
|
|
|
|
||
194. Найти радиус сходимости
ряда
|
|
100 |
10 |
1 |
|
||
195. Найти интервал сходимости ряда |
|
|
|
|
|
||
196. Как называется множество, содержащего всех своих предельных точек? |
Замкнутым |
Открытым |
Полузамкнутым |
Полуоткрытым |
|
||
197. Как называется
множество
|
Интервал |
Полу интервал |
Сегмент |
Полу сегмент |
|
||
198. Если
|
Ограничена |
Не ограничена |
Монотонно возрастает |
Монотонна |
|
||
199. При выполнении какого из условий ряд сходится по признаку Коши? |
|
|
|
|
|
||
200. При выполнении какого из условий ряд сходится по признаку Даламбера? |
|
|
|
|
|
||

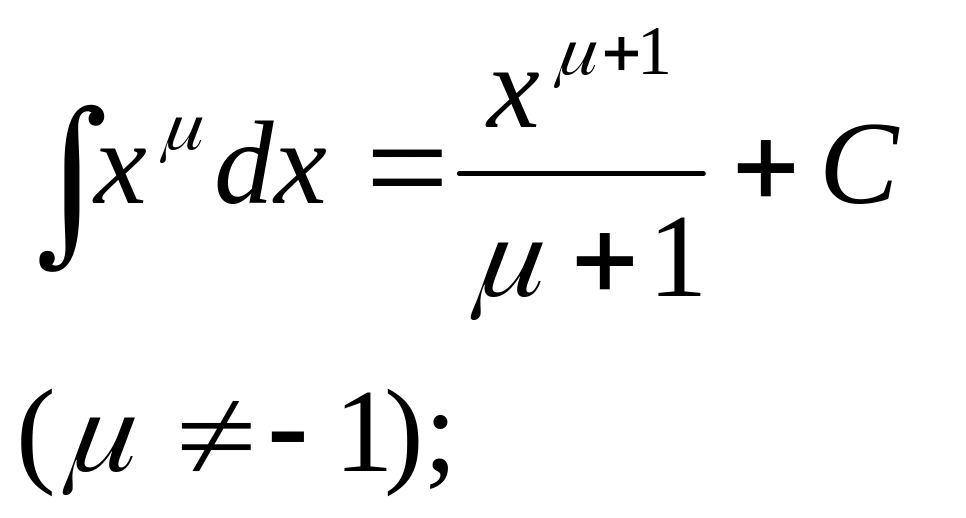
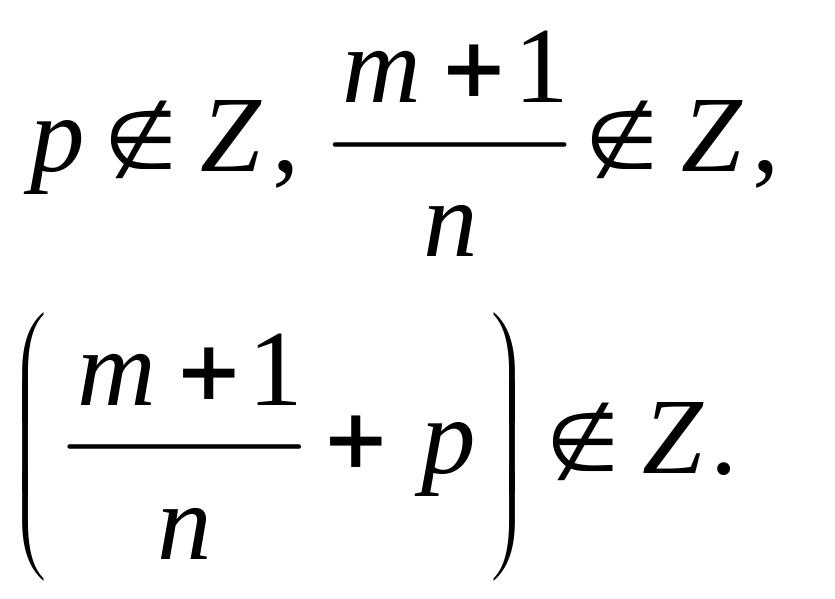
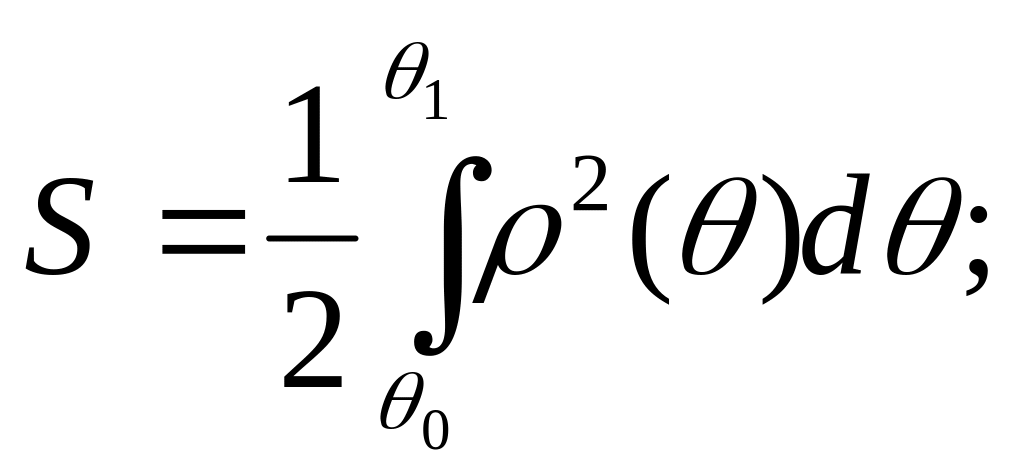
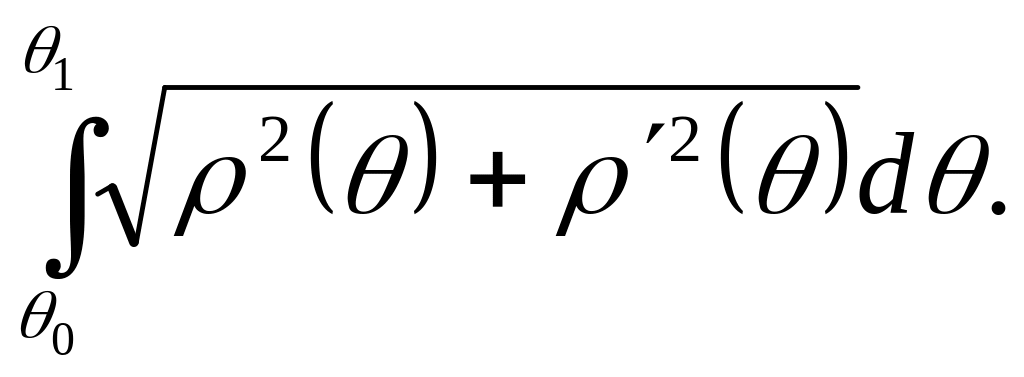
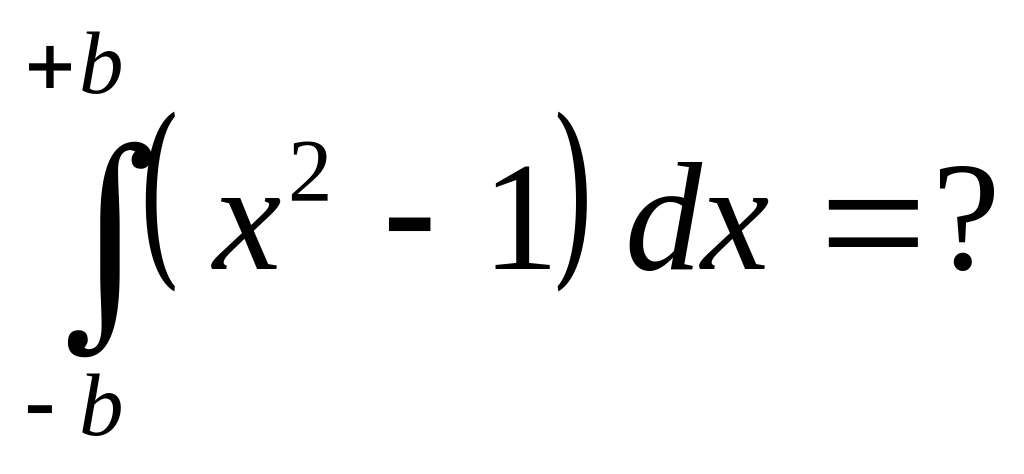
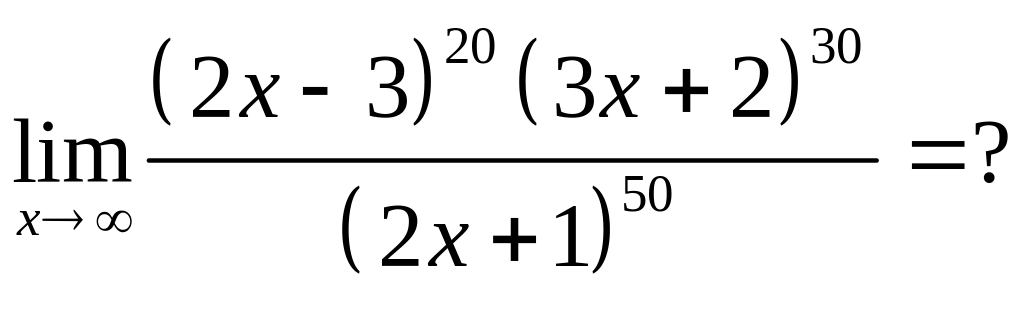
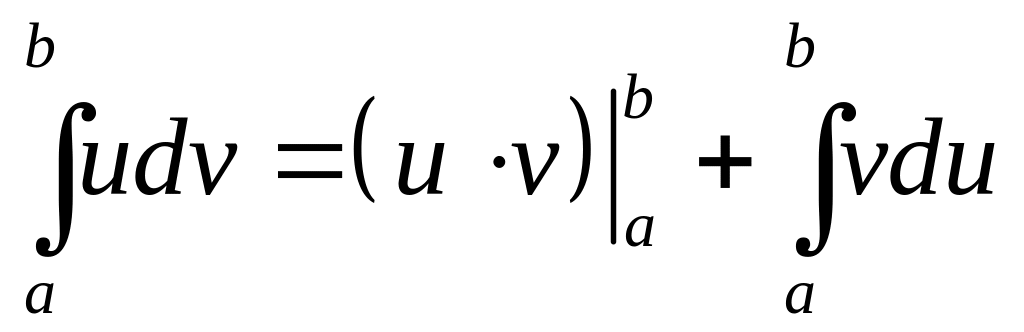

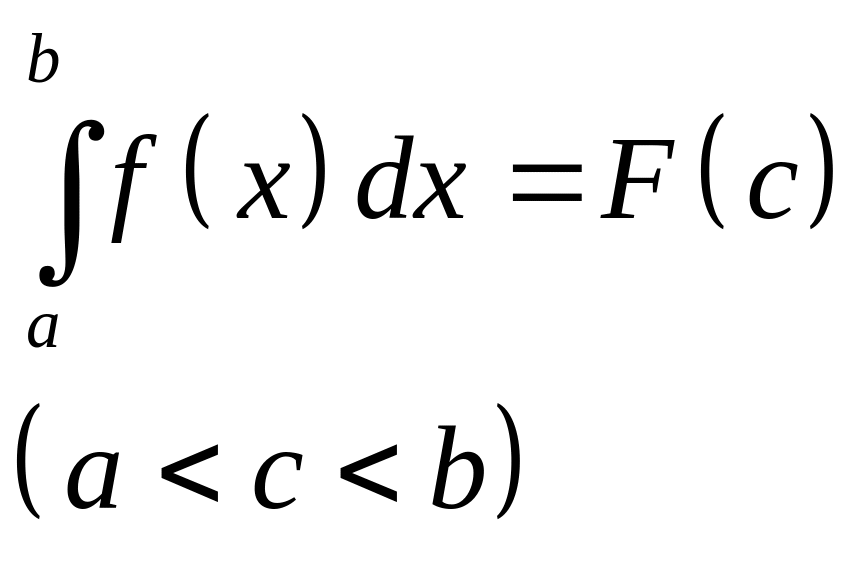
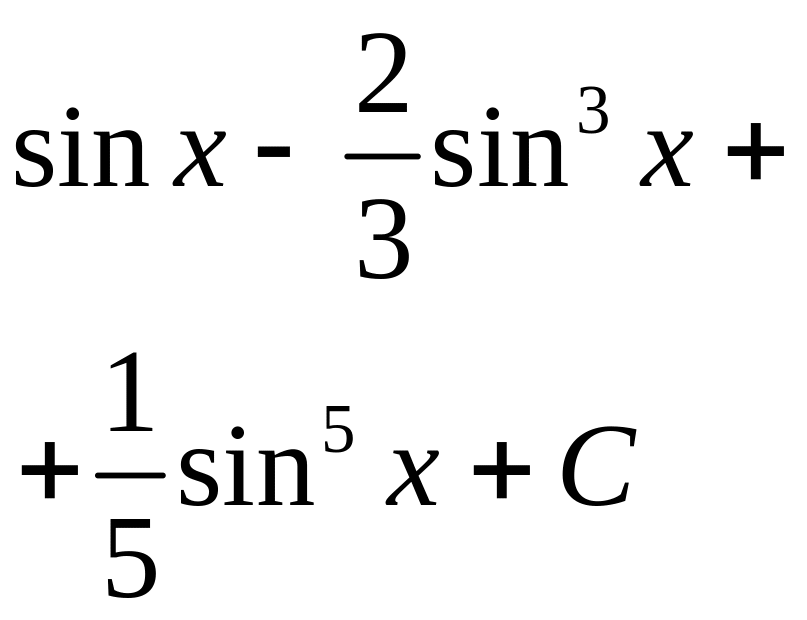
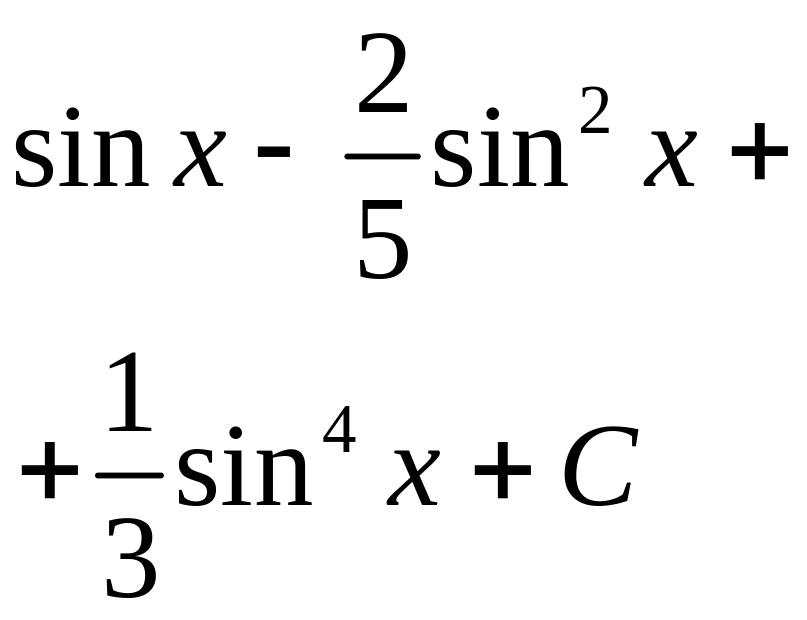
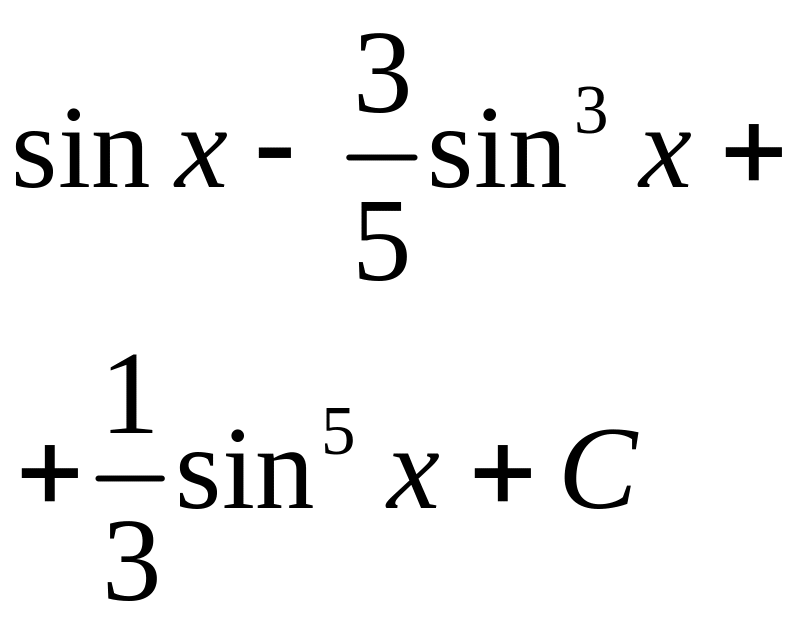
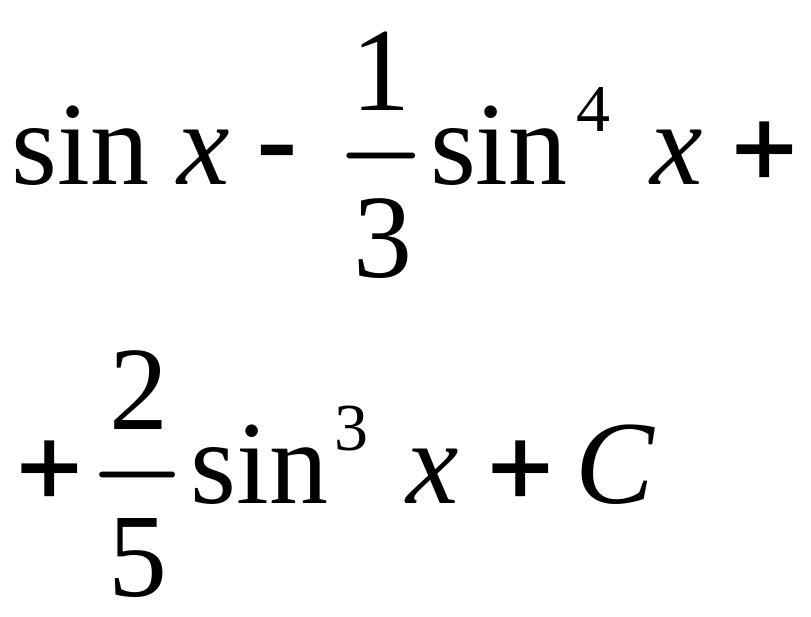
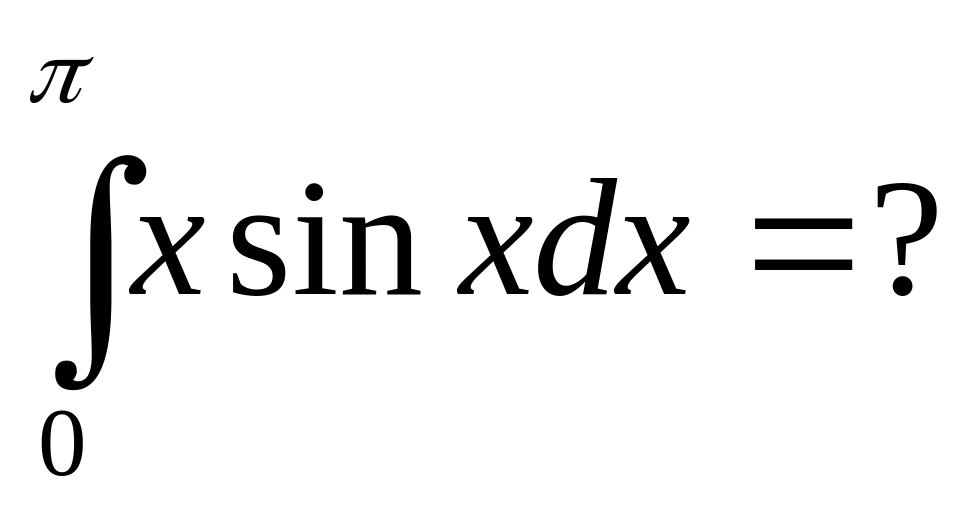
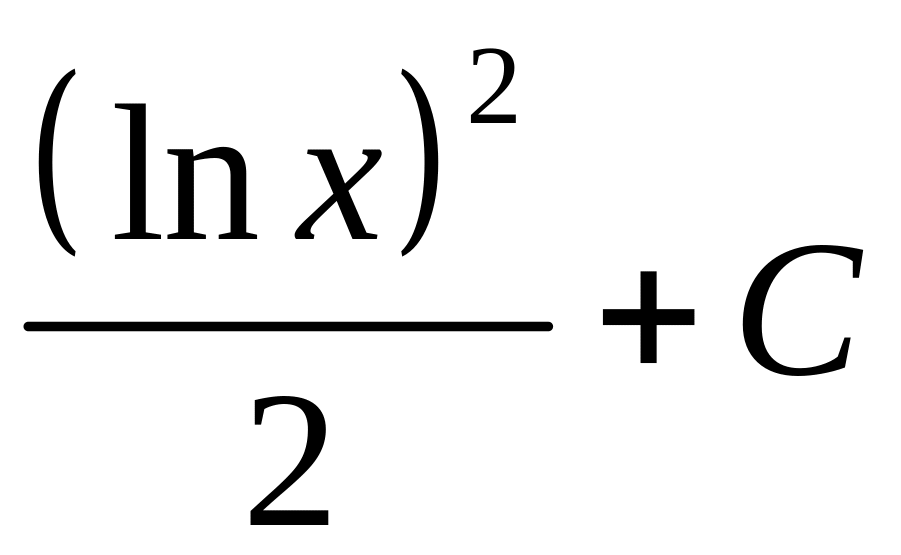
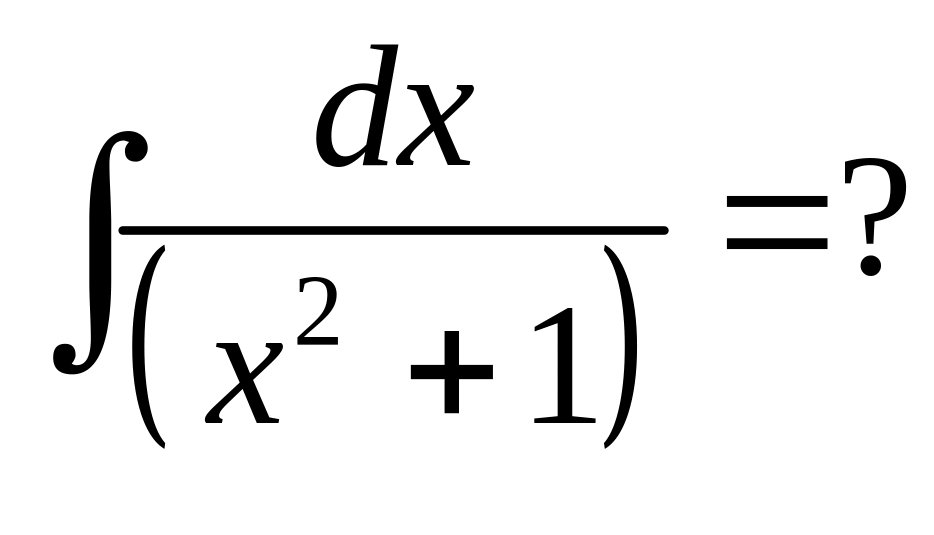
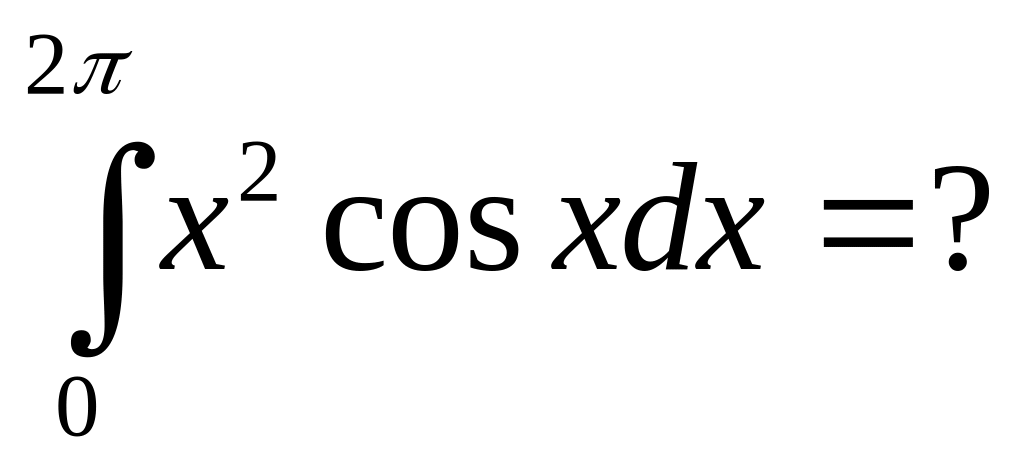
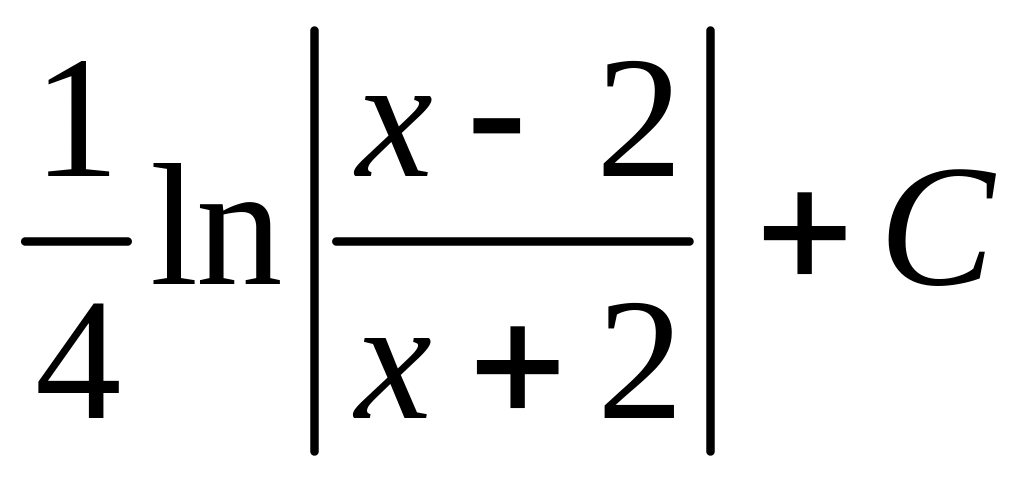
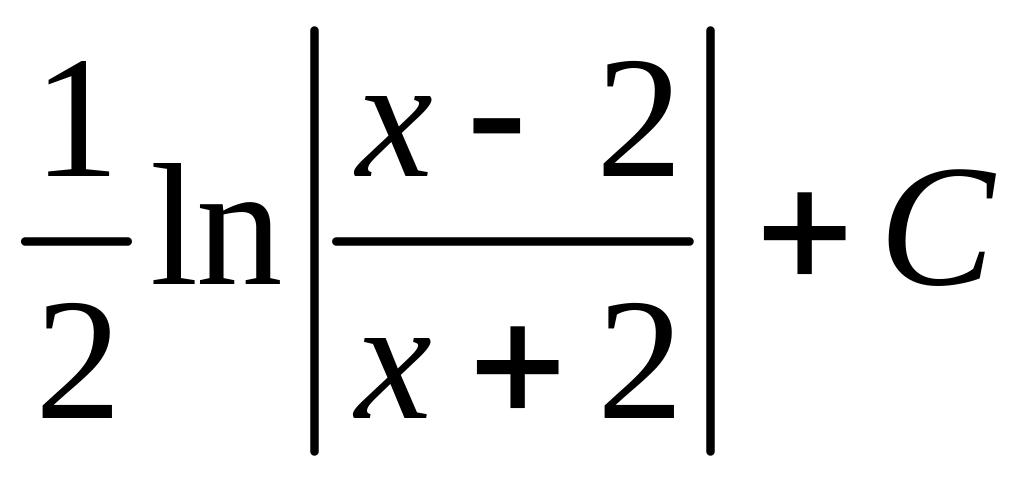
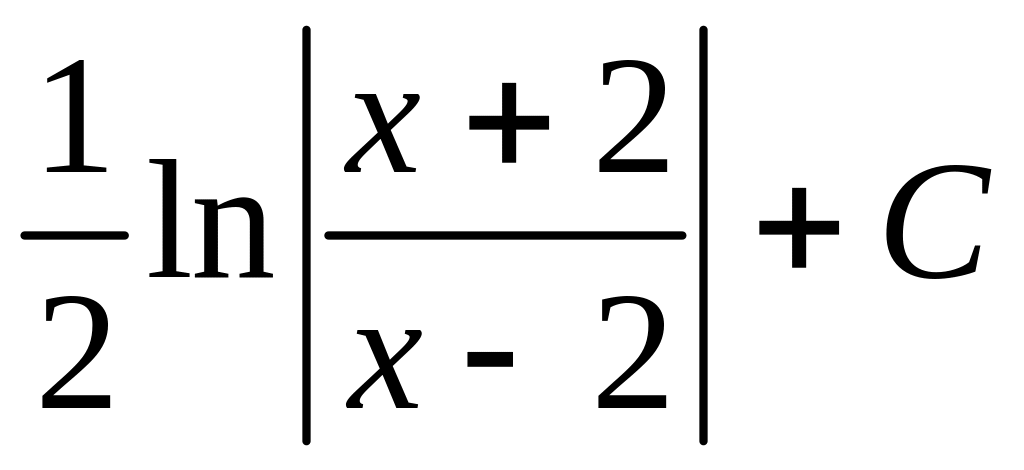

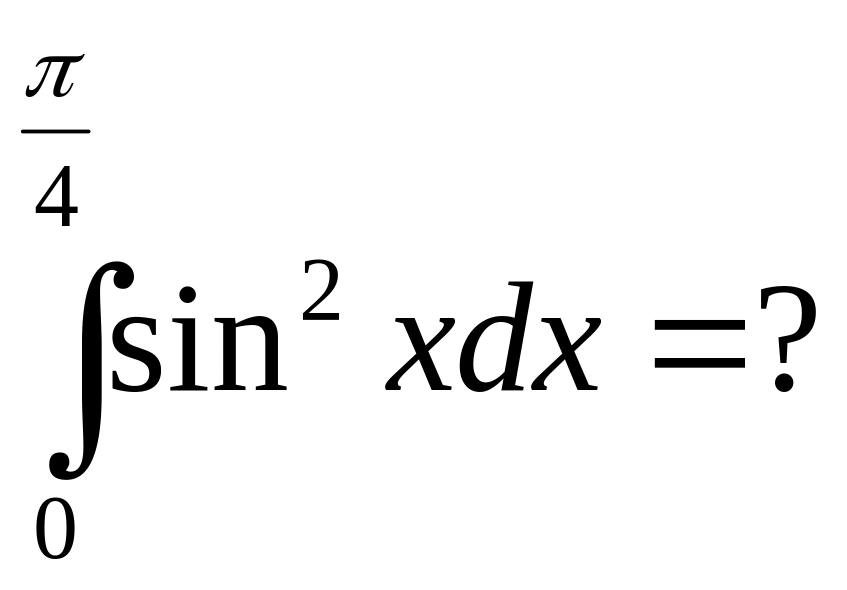
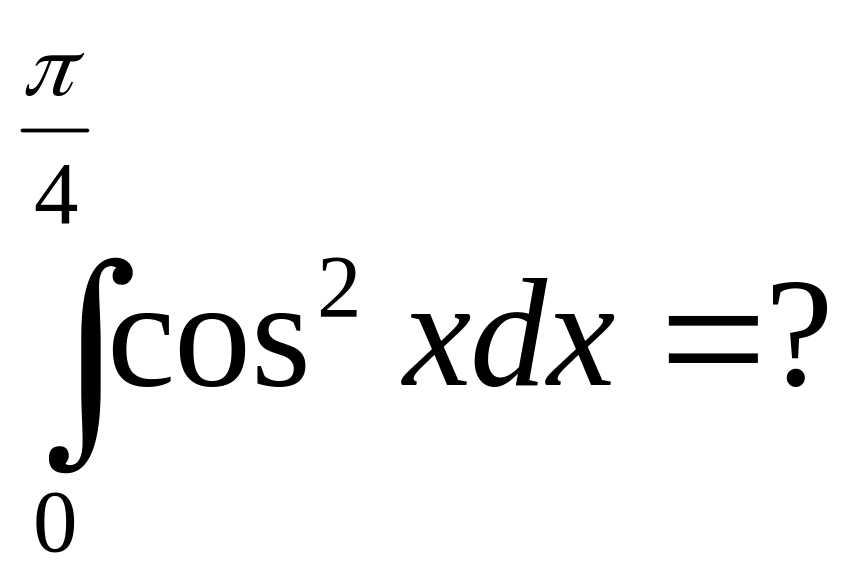
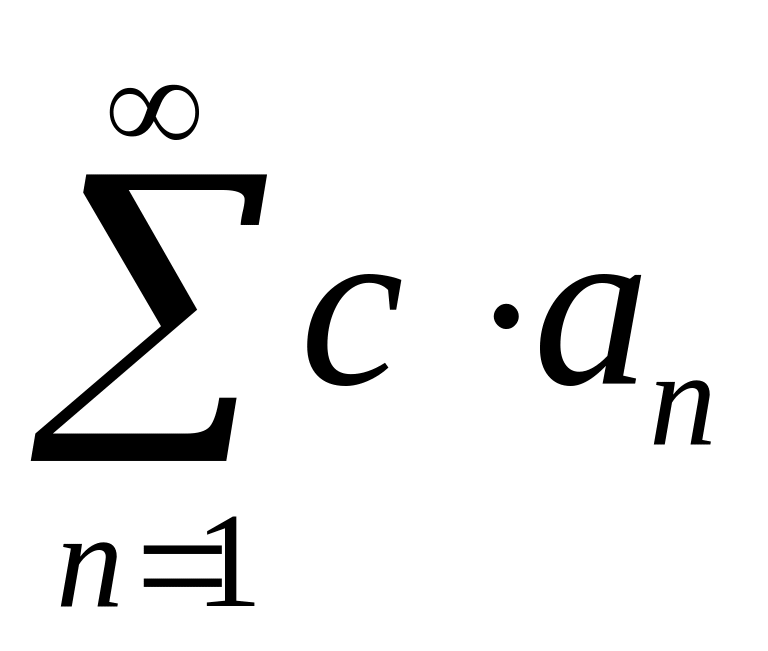
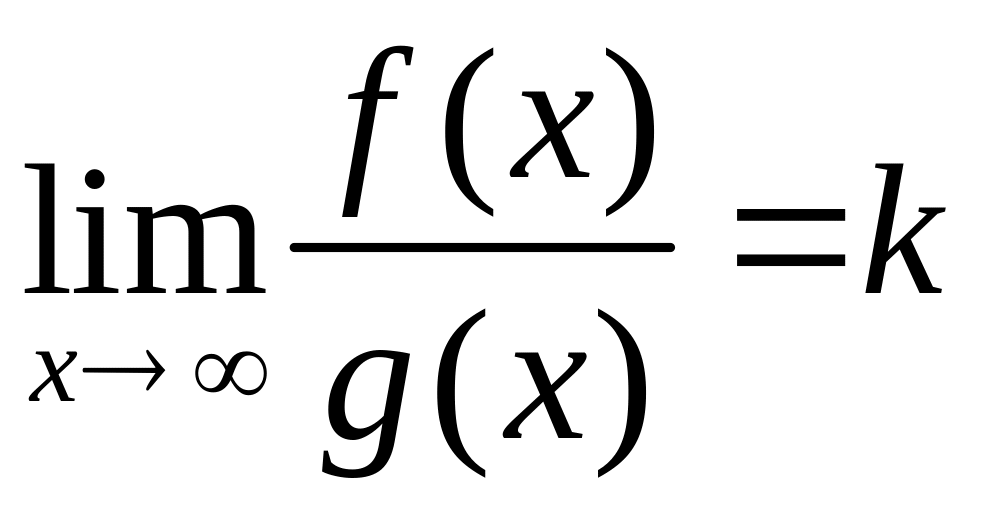 .
При каких значениях
.
При каких значениях
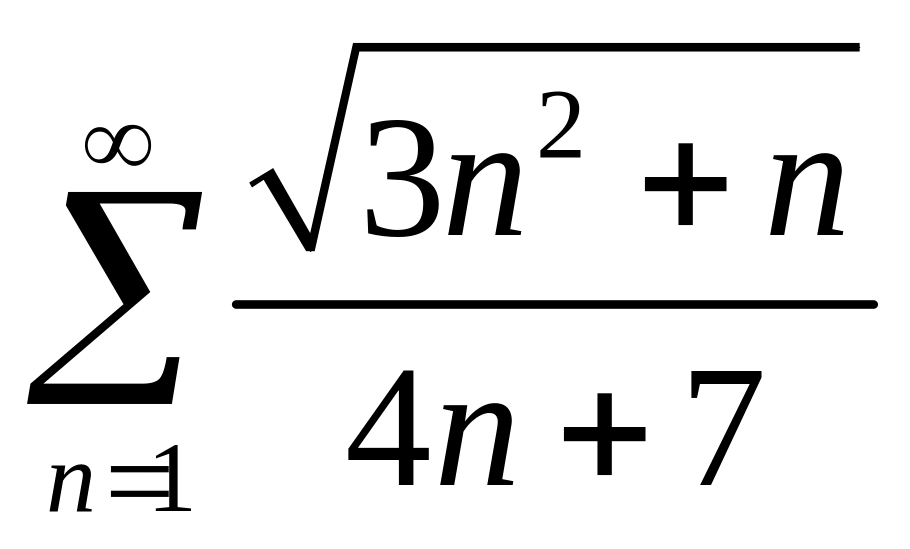
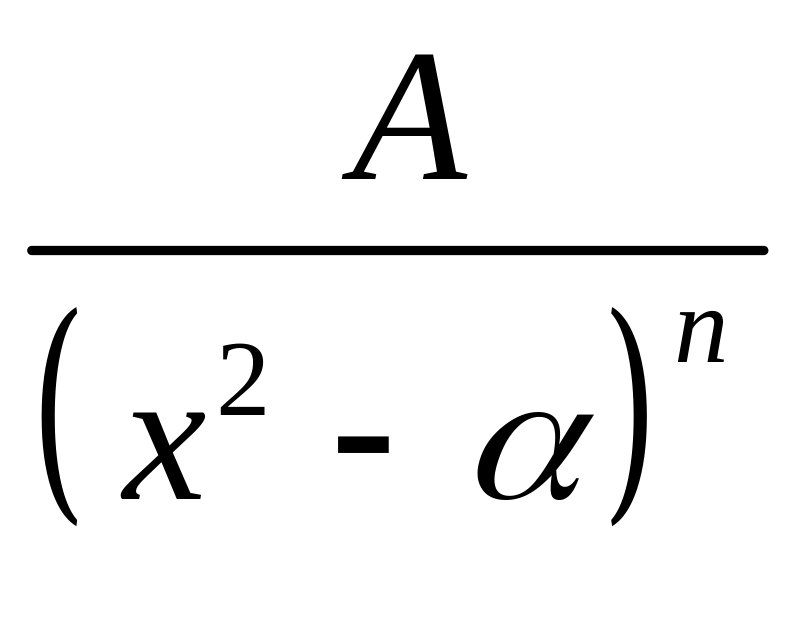 .
.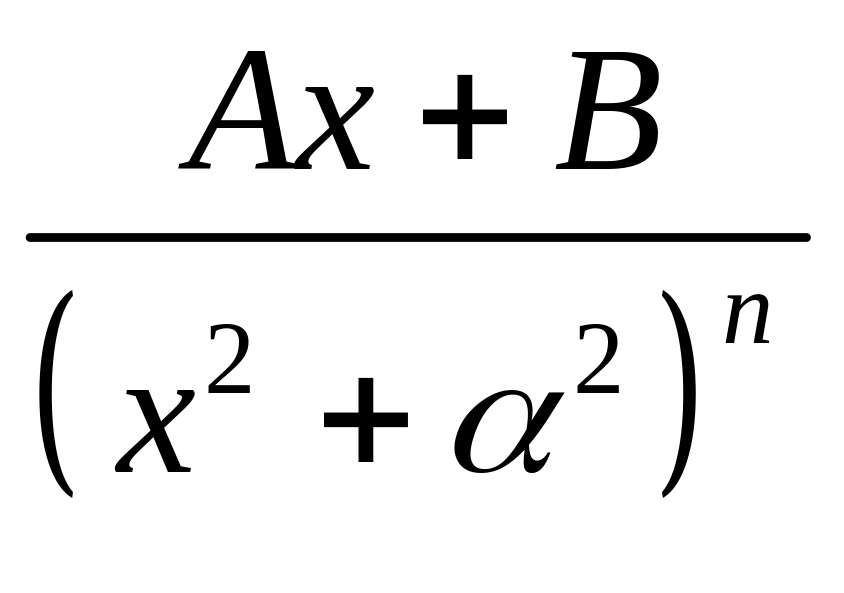 ;
4)
;
4)