Выполнение критериальных проверок
Проверим значимость коэффициентов полученной квазилинейной модели с целью исключения из модели факторов, слабо влияющих на функцию отклика.
Вычислим дисперсию наблюдения:
Дисперсии оценки коэффициентов модели:
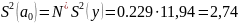
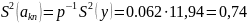
При
количестве опытов в плане
и количестве повторных
опытов
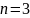число степеней свободы равно
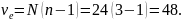Выбираем доверительную вероятность
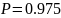и определяем по таблице из приложения
1 значение коэффициента Стьюдента
.
Доверительный интервал коэффициентов аl модели
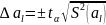
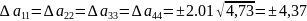
Коэффициент
модели значим, если абсолютная величина
больше доверительного интервала, т.е.
.
Окончательный вид модели:
Проверка адекватности регрессионной модели
Обозначим
через
дисперсию в i-й точке,
– сумму квадратов ошибок в i-й точке.
В качестве примера вычислим и в третьей точке опыта:
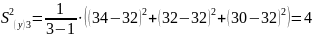
Дисперсия наблюдения:
Дисперсия адекватности:
Данные для расчёта дисперсии
№ |
|
|
|
|
|
|
|
|
|
|
|
1 |
-1 |
-1 |
-1 |
-1 |
52 |
48 |
54 |
51,33333 |
9,333333 |
56,45367 |
97,32011 |
2 |
-1 |
-1 |
-1 |
1 |
54 |
56 |
60 |
56,66667 |
9,333333 |
65,34033 |
244,3641 |
3 |
-1 |
-1 |
1 |
-1 |
34 |
32 |
30 |
32 |
4 |
44,32433 |
463,6676 |
4 |
-1 |
-1 |
1 |
1 |
60 |
56 |
58 |
58 |
4 |
53,211 |
76,80356 |
5 |
-1 |
1 |
-1 |
-1 |
21 |
19 |
19 |
19,66667 |
1,333333 |
33,983 |
617,5389 |
6 |
-1 |
1 |
-1 |
1 |
48 |
46 |
53 |
49 |
13 |
42,86967 |
138,743 |
7 |
-1 |
1 |
1 |
-1 |
42 |
38 |
36 |
38,66667 |
9,333333 |
37,97367 |
20,10741 |
8 |
-1 |
1 |
1 |
1 |
26 |
31 |
24 |
27 |
13 |
46,86033 |
1209,299 |
9 |
1 |
-1 |
-1 |
-1 |
52 |
54 |
56 |
54 |
4 |
51,60167 |
25,25601 |
10 |
1 |
-1 |
-1 |
1 |
42 |
34 |
37 |
37,66667 |
16,33333 |
42,715 |
109,1237 |
11 |
1 |
-1 |
1 |
-1 |
22 |
24 |
20 |
22 |
4 |
39,47233 |
923,8473 |
12 |
1 |
-1 |
1 |
1 |
26 |
29 |
33 |
29,33333 |
12,33333 |
30,58567 |
29,37168 |
13 |
1 |
1 |
-1 |
-1 |
24 |
25 |
21 |
23,33333 |
4,333333 |
29,131 |
109,5055 |
14 |
1 |
1 |
-1 |
1 |
15 |
16 |
17 |
16 |
1 |
20,24433 |
56,0431 |
15 |
1 |
1 |
1 |
-1 |
28 |
29 |
26 |
27,66667 |
2,333333 |
33,12167 |
93,93774 |
16 |
1 |
1 |
1 |
1 |
21 |
22 |
21 |
21,33333 |
0,333333 |
24,235 |
25,92567 |
17 |
1 |
0 |
0 |
0 |
37 |
42 |
40 |
39,66667 |
6,333333 |
45,64967 |
120,0555 |
18 |
-1 |
0 |
0 |
0 |
59 |
62 |
63 |
61,33333 |
4,333333 |
59,38833 |
20,01574 |
19 |
0 |
1 |
0 |
0 |
36 |
38 |
34 |
36 |
4 |
36,861 |
10,22396 |
20 |
0 |
-1 |
0 |
0 |
43 |
59 |
37 |
46,33333 |
129,3333 |
51,27167 |
331,8281 |
21 |
0 |
0 |
1 |
0 |
44 |
40 |
46 |
43,33333 |
9,333333 |
35,651 |
195,7214 |
22 |
0 |
0 |
-1 |
0 |
25 |
28 |
31 |
28 |
9 |
39,72033 |
430,0986 |
23 |
0 |
0 |
0 |
1 |
34 |
29 |
33 |
32 |
7 |
38,68567 |
148,0944 |
24 |
0 |
0 |
0 |
-1 |
38 |
42 |
44 |
41,33333 |
9,333333 |
38,68567 |
39,69708 |
|
|
|
|
|
|
|
|
|
286,6667 |
|
5536,58 |
Вычисляем F-статистику Фишера по формуле:
По
таблице П1.3 для
и
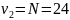находим
.
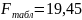Так
как
,
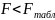то гипотеза об адекватности модели не
отвергается. Модель адекватна.