МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра автоматизированных систем управления (АСУ)

Контрольная работа № 1

по предмету «Концепции современного естествознания»

Преподаватель Студент группы

___________ / /

___________2008 г. _______________ 2008 г.

Орск 2008

1. Что такое «научная программа»? Как развивалась математическая научная программа? Каково значение математического моделирования в естествознании?

Понятие «научная программа» сформировалось в методологии науки. Научная программа, включающая в себя систему единых принципов, претендует на всеобщий охват и объяснение всех явлений. В отличие от философской системы она определяет не только характеристику предмета исследования, но и возможность методов проверки заявленных принципов, без чего они не станут теорией. Научные программы связывают научные картины мира с умонастроениями в обществе, задают идеал научного объяснения и организации знания, положения, которые считают доказанными или достоверными. Связь эволюции науки с материальной и духовной культурой общества отражена в том, что научные революции не вытекали из логики развития науки.

Первые научные программы сформировались в Древней Греции с VI по III в. до н. э. и надолго определили развитие науки. К ним относятся математическая, континуальная и атомистическая НП. Каждая программа формировалась в несколько этапов.

Математическая программа выросла из философии Пифагора и Платона, континуальная — началась с Аристотеля, с его физической школы перипатетиков, и просуществовала до науки Нового времени, т. е. почти 20 веков. Атомистическая программа, идущая от представлений Демокрита и Эпикура, стала активно развиваться после XVII в. Но ранние пифагорейские представления отличны от программы Платона. Данные изменения связаны с развитием общества за 300 лет. За это время произошел перелом в мышлении, связанный с философией эгейской школы, когда возникли первые (из известных нам) попытки критики оснований знания. Изменения в социальной жизни Эллады существенно повлияли на общемировоззренческие ориентиры ученого, на его понимание природы и места человека в ней, а отсюда и на научное мышление, на методы исследований и формирование идеалов и норм научного познания. Этический индивидуализм («индивидуум» — латинский перевод греческого «атом») и естественно-научный атомизм в XVII—XVIII вв. воспринимались как две стороны одного мировосприятия: самостоятельные индивиды (атомы, корпускулы) управляются механическим образом и регулируются жестким внешним законом. И механическая картина мира с законом тяготения Ньютона рассматривалась экономистами как природное обоснование экономических учений. Так, Адам Смит считал, что частнопредпринимательский интерес соответствует моральной гравитации.

Поскольку материальный мир един и подчиняется простым законам, не имеет цели развития, не способен ставить человеку цели, человек обретает свободу выбора цели сам. И наибольшей ценностью данной программы являлось ее нравственное значение, а вовсе не эффективность решения научных или практических задач. В мире атомистической программы человек мог свободно действовать, отвечая за последствия своих деяний, он стал полновластным хозяином вещей. Идея механистичности природы связана у Р.Бойля, Р.Декарта и других мыслителей и ученых XVII в. с признанием уникальности человека и ответственности его как единственного сознательного начала в природе. Именно человеку вменена «обязанность» заботы о ее спасении и дано право познавать природу и господствовать над нею. Эта позиция отвечала потребностям материального производства периода раннего капитализма, она формировала иное поведение и обосновывала его.

Моделирование – метод научного познания, основанный на изучении реальных объектов посредством изучения моделей этих объектов, т.е. посредством изучения более доступных для исследования и (или) вмешательства объектов-заместителей естественного или искусственного происхождения, обладающих свойствами реальных объектов.

При мысленном (образном) моделировании свойства реального объекта изучаются через мысленно-наглядные представления о нем (с этого варианта моделирования начинается, вероятно, любое первое изучение интересующего объекта).

При физическом (предметном) моделировании модель воспроизводит определенные геометрические, физические, функциональные свойства реального объекта, при этом являясь более доступной или удобной для исследования благодаря отличию от реального объекта в некотором не существенном для данного исследования плане (например, устойчивость небоскреба или моста, в некотором приближении, можно изучать на сильно уменьшенной физической модели – рискованно, дорого и вовсе не обязательно «крушить» реальные объекты).

При знаковом моделировании модель, являющаяся схемой, графиком, математической формулой, воспроизводит поведение определенной интересующей характеристики реального объекта благодаря тому, что существует и известна математическая зависимость этой характеристики от прочих параметров системы (построить приемлемые физические модели изменяющегося земного климата или электрона, излучающего электромагнитную волну при межуровневом переходе – задача безнадежная; да и устойчивость небоскреба, вероятно, неплохо заранее просчитать поточнее).

По степени адекватности модели прототипу их принято подразделять на эвристические (приблизительно соответствующие прототипу по изучаемому поведению в целом, но не позволяющие дать ответ на вопрос, насколько интенсивно должен происходить тот или иной процесс в реальности), качественные (отражающие принципиальные свойства реального объекта и качественно соответствующие ему по характеру поведения) и количественные (достаточно точно соответствующие реальному объекту, так что численные значения исследуемых параметров, являющиеся результатом исследования модели, близки к значениям тех же параметров в реальности).

Свойства любой модели не должны, да и не могут, точно и полностью соответствовать абсолютно всем свойствам соответствующего реального объекта в любых ситуациях. Для изучения устойчивости того же небоскреба, вероятно, в любом случае нет необходимости заботиться о соответствии физической модели реальному объекту по силе светового давления на нее, или по силе ее гравитационного взаимодействия с Солнцем, или об удовлетворительном отражении моделью свойств оригинала в ситуации, когда небоскреб начинают скручивать винтом или кидают в него обломки космической станции. В математических моделях любой дополнительный параметр может привести к существенному усложнению решения соответствующей системы уравнений, к необходимости применения дополнительных допущений, отбрасывания малых членов и т.п., при численном моделировании непропорционально вырастает время обработки задачи компьютером, нарастает ошибка счета. Таким образом, при моделировании является существенным вопрос об оптимальной, для данного конкретного исследования, степени соответствия модели оригиналу по вариантам поведения исследуемой системы, по связям с другими объектами и по внутренним связям исследуемой системы; в зависимости от вопроса, на который хочет ответить исследователь, одна и та же модель одного и того же реального объекта может быть признана адекватной или абсолютно не отражающей реальность.

В силу сложности внутренних и внешних связей любого реального объекта и (или) его модели, возможного наличия на первый взгляд незаметных, но чрезвычайно критичных (в плане реальности результатов исследования) свойств реального объекта и (или) модели, вопрос о выборе модели, действительно адекватной цели исследования и действительно «грубой» по отношению к неизбежным ошибкам и погрешностям исследования, требует большой осторожности.

Можно привести следующий пример, дающий наглядное представление о том, насколько легко превратить исследование в пустую трату времени и ресурсов, если выбрать «не подходящую» для данного исследования (или недостаточно изученную) математическую модель. Пусть некоторый процесс в действительности описывается функцией [pic], однако исследователю известно лишь то, что процесс должен описываться полиномом 20-й степени, и в ходе исследования значение каждого из коэффициентов перед [pic] подбирается на основании данных натурных измерений, статистических, расчетных и иных данных. Количество интересующих событий за определенный период предполагается равным количеству действительных корней полинома, а их интенсивность - модулю значения соответствующего корня (в действительности – 20 корней (например, 20 извержений вулкана в год) с интенсивностью 1, 2, … 20). Оказывается, что ошибка на [pic] (измерительная, счетная …- любая) при определении коэффициента перед [pic] (составляющая порядка [pic] от «вполне макроскопического» искомого коэффициента 210.00000000… и порядка [pic] от последнего члена полинома 20!) «скроет» от исследователя 10 из 20 искомых событий (извержений), причем «исчезнет» большая часть наиболее сильных извержений интенсивностью 10, 11, … , 19 (корни полинома станут комплексными с большими мнимыми частями). Примером одной из моделей, обсуждаемых как минимум в течение более чем двух столетий, является модель демографического взрыва: в конце 18 века Мальтус впервые поднял вопрос о росте численности человечества по экспоненте. Если Мальтуса беспокоило только несоответствие роста населения росту производства пищи, то в настоящее время возникает множество иных, инициированных исключительно самим человеком, проблем: истощение запасов минерального топлива, уничтожение лесов и рост концентрации углекислоты в атмосфере, уменьшение защищающей человека от ультрафиолета озоносферы, общее загрязнение окружающей среды, ведущее к так называемому «размыванию генофонда» человечества и т.д. В такой ситуации моделирование роста численности населения так называемой логистической кривой [pic], выводящей численность населения на константу [pic] при [pic], выглядит весьма оптимистическим прогнозом. У любой саморегулирующейся системы существует порог стабильности, и каков он для земной биосферы, для которой новый, человеческий влияющий фактор стал основным – сказать сложно. Как это весьма наглядно показывает предыдущий пример с «превращением» действительных корней полинома в комплексные, для качественного перехода систем в принципиально иное состояние иногда необходимо весьма небольшое изменение параметров. Остается надеяться, что homo sapiens («человек разумный») достаточно разумен для того, чтобы ограничить свое вредное влияние на свою собственную сферу обитания, и его реальная (действительная) жизнь, благодаря ему же самому, не сменится на жизнь «комплексную», содержащую большую i - (от imaginary - мнимую, нереальную) составляющую.

2. Сформулируйте основные законы классической механики материальной точки. Как моделируется система, состоящая из двух и более материальных точек? Приведите примеры задач, в которых можно считать Землю материальной точкой и примеры, в которых нельзя.

Динамика – это раздел классической механики, изучающий движение материальных тел под действием приложенных к ним сил, т.е. дающий связь между взаимодействиями тел и изменениями в их движении. Она является основным разделом механики и базируется на трех законах Ньютона (1687 г.)      Первый закон Ньютона (закон инерции) формулируется следующим образом: всякое тело (материальная точка) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.      Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при отсутствии или взаимном уравновешивании внешних воздействий называется инертностью. Если на тело действует неуравновешенная система сил, то инертность сказывается в том, что изменение состояния покоя или движения тела происходит постепенно, а не мгновенно. При этом движение изменяется тем медленнее, чем больше инертность тела. Мерой инертности тела при поступательном движении является масса.

Первый закон Ньютона выполняется не во всякой системе отсчета. Системы, в которых он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система, относительно которой свободная материальная точка, не подверженная воздействию других тел, движется равномерно и прямолинейно, или по инерции. Система отсчета, движущаяся по отношению к инерциальной системе отсчета с ускорением, является неинерциальной, и в ней не выполняются ни закон инерции, ни второй закон Ньютона, ни закон сохранения импульса.

Понятие «инерциальная система отсчета» является научной абстракцией. Реальная система отсчета всегда связывается с каким-нибудь конкретным телом (Землей, корпусом корабля и т.п.), по отношению к которому и изучается движение тех или иных объектов. Однако в природе нет неподвижных тел (тело, неподвижное относительно Земли, будет двигаться вместе с нею ускоренно по отношению к Солнцу и звездам), поэтому любая реальная система отсчета может рассматриваться как инерциальная лишь с той или иной степенью приближения. С очень высокой степенью точности инерциальной можно считать гелиоцентрическую (звездную) систему с началом координат в центре Солнца и с осями, направленными на три звезды. Для решения большинства технических задач инерциальной системой можно считать систему отсчета, жестко связанную с Землей (не учитывается вращение Земли вокруг собственной оси и вокруг Солнца).

Масса – это физическая величина, определяющая инерционные свойства материи. Масса – это свойство самого тела и, в отличие от веса, не зависит от места ее измерения  (вес Р тела в разных точках земного шара различен: он максимален на полюсах и минимален на экваторе). Ускорение свободного падения g тел на Землю также зависит от географической широты места наблюдения и от его  высоты над уровнем моря. Однако отношение веса тела Р к его ускорению g одинаково во всех точках земного шара. Это отношение и принято для количественного измерения массы:

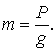
За единицу массы принят килограмм массы, равный массе эталона, сделанного из сплава иридия и платины. Следует отметить, что масса тела считается постоянной величиной только в классической механике Ньютона, изучающей движение тел со скоростями, небольшими по сравнению со скоростью света ( ). В современной физике установлено, что масса тела увеличивается с увеличением скорости его движения по закону:

 

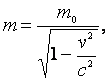
где m – масса тела, движущегося со скоростью ; с – скорость света; m0 – масса покоящегося тела. Из формулы следует, что вес тела:

,

т.е. вес – это сила, с которой тело притягивается Землей, т.е. та сила, которая сообщает телу ускорение g=9,81 м/с2:

1 кГ=1 кг·9,81 м/с2.

С другой стороны, 1 Н=1 кг·1 м/с2 , следовательно, 1 кГ=9,81 Н.

Для описания воздействий тел (материальных точек) друг на друга вводится понятие силы. Под действием сил тела либо изменяют скорость движения, т.е. приобретают ускорения (динамическое проявление сил), либо деформируются, т.е. изменяют свою форму и размеры (статическое проявление сил). Таким образом, сила - это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате, которого тело приобретает ускорение или изменяет свою форму и размеры. В каждый момент времени сила характеризуется числовым значением (модулем), направлением в пространстве и точкой приложения.

Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение материального объекта (точки, тела) под действием приложенных к нему сил.      В динамике рассматриваются два типа задач, решения которых находятся на основе второго закона Ньютона. Задачи первого типа состоят в том, чтобы, зная движение тела, определить действующие на него силы. Классическим примером решения такой задачи является открытие Ньютоном закона всемирного тяготения: зная установленные Кеплером на основании результатов наблюдений законы движений планет, Ньютон доказал, что это движение происходит под действием силы, обратно пропорциональной квадрату расстояния между планетой и Солнцем.

Задачи второго типа являются в динамике основными и состоят в том, чтобы по действующим на тело силам определить закон его движения (уравнение движения). Для решения этих задач необходимо знать начальные условия, т.е. положение и скорость тела в момент начала его движения под действием заданных сил. Примерами таких задач являются следующие: а) по величине и направлению скорости снаряда в момент его вылета из канала ствола и действующим на снаряд при его движении силе тяжести и силе сопротивления воздуха найти закон движения снаряда, в частности его траекторию, горизонтальную дальность полета, время движения до цели; б) по известным скорости автомобиля в момент начала торможения и силе торможения найти время движения и путь до остановки.

Второй закон Ньютона формулируется следующим образом: ускорение, приобретаемое материальной точкой (телом), прямо пропорционально действующей силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела):

где  - коэффициент пропорциональности, зависящий от выбора системы единиц. В Международной системе (СИ) =1, поэтому

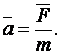
Второй закон Ньютона обычно записывается в следующей форме:

    

или .    

Вектор называется импульсом или количеством движения. В отличие от ускорения и скорости, импульс является характеристикой движущегося тела, отражающей не только кинематическую меру движения (скорость), но и его важнейшее динамическое свойство – массу.

Таким образом, можно записать:

Выражение является более общей формулировкой второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе.

Это уравнение называется уравнением движения материальной точки. Единица силы  в системе СИ – ньютон (Н): 1 Н – это сила, которая телу массой в 1 кг сообщает ускорение 1 м/с2 в направлении действия силы: 1 Н = 1 кг·1 м/с2.

При действии на материальную точку нескольких сил справедлив принцип независимости действия сил: если на материальную точку действуют одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, определяемое вторым законом Ньютона так, как если бы других сил не было:

где сила  называется равнодействующей сил или результирующей силой. Таким образом, если на тело действует одновременно несколько сил, то, согласно принципу независимости действия сил, под силой  во втором законе Ньютона понимают результирующую силу.

Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго закона: в случае равенства нулю равнодействующей силы ускорение также равно нулю, т.е. тело находится в покое или движется равномерно.

Воздействие тел (материальных точек) друг на друга всегда является взаимным и определяется третьим законом Ньютона (законом о равенстве действия и противодействия): действия двух тел друг на друга всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти тела:

где - сила, действующая на первое тело со стороны второго;  - сила, действующая на второе тело со стороны первого.

Необходимо помнить, что силы  и  приложены к разным телам (материальным точкам) и поэтому не уравновешивают друг друга; они действуют парами и являются силами одной природы.

Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.

Из второго и третьего законов Ньютона вытекает закон сохранения импульса замкнутой системы. Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы (они взаимно уравновешиваются), называется замкнутой или изолированной. В такой системе необходимо учитывать только силы взаимодействия между входящими в нее телами (внутренние силы). Строго говоря, изолированных механических систем в природе не существует.

Закон сохранения импульса справедлив не только в классической механике; он выполняется и для замкнутых систем микрочастиц, т.е. действует и в квантовой механике. Другими словами, этот закон носит универсальный характер и является фундаментальным законом природы.      Закон сохранения импульса является следствием однородности пространства: при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, т.е. не зависят от выбора положения начала координат инерциальной системы отсчета.