3.4 Расчет исходного механизма

Подвижным звеном здесь является кривошип 2, который представляет собой зубчатое колесо с числом зубьев Z₂, с установленным на нем пальцем В - шейкой кинематической пары 2-3.

Кривошипное колесо находится в равновесии под действием следующих и реакций связей.

R₃₂-реакция третьего звена на кривошип. Величина определена при решении предыдущей группы. Направление ее противоположно R₂₃.

G₂-силы тяжести звена 2,

G₂ = 500 Н.

P₁₂-реакция стойки на кривошип. Полностью неизвестная величина. определяется после построения плана сил;

P_ур - уравновешивающая сила-реакция зуба отброшенной шестерни, число зубьев которой Z₁.

Величина уравновешивающей силы может быть найдена из суммы моментов относительно точки А.

P_ур·h=P₃₂·h_ур; (3.10)

P_ур = P₃₂·h / h_ур = 41250∙83,2/80 = 42900 H.

План сил, построен по векторному равенству

P₃₂ + G₂ + R₁₂ + P_УР = 0, (3.11)

P₁₂= 83000 H.

Аналогично проводим расчет для положения 9 (холостой ход механизма).

Группа 5-6:

Р_С + Р_И5 + Р_И6 + G₆ + G₅ + R₁₆ + R₄₅ = 0

Р_С = 370 Н,

G₆ = 370 Н,

G₅ = 0 Н,

Р_И5 = 0,

Р_И6 = 37∙36 = 1332 Н,

R^T₄₅ = 0.

R₄₅ = 2089 Н,

R₁₆ = 722,8 Н,

Группа 3-4:

R₅₄ + R₁₄ + G₃ + P_И3 + R^T₂₃ + R^N₂₃

R₅₄ = 2089 Н,

G₃ = 49·10 = 490 Н;

G₄ = 7.9·10 = 79 Н;

P_И3 = 49∙11,5 = 563,5 Н,

P_И4 = 7.9∙5,8 = 45,8 Н,

M_И3 = 0.35·156,7 = 54,8 Н·м;

M_И4 = 0.1·70,6 = 7,06 Н·м;

R^T₂₃ = (G₃∙h + P_ИЗ∙h₄ + M_И3) / ВС = (490∙78,5 + 563,5∙86,4 +54,8)/270 =

323 Н,

R^T₁₄=(R₅₄∙h₃ - G₄∙h₁ - Р_ин4∙h₂ + M_И4)/DC = (2089∙86,4-79∙76-45,8∙69+7,06)/270 = 634,5 Н,

R₂₃ = 5150 Н,

R₁₄ = 2940 Н.

Исходный механизм:

R₃₂ + G₂ + R₁₂ + P_УР = 0,

R₃₂ = R₂₃ = 5150 H,

G₂ = 500 Н,

P_ур = P₃₂·h / h₁ = 5150∙75,5/80 = 4860,3 H.

R₁₂ = 2310 Н.

4 Расчет замкнутого эпициклического механизма

Определение неизвестных чисел зубьев.

Определение передаточного числа планетарного механизма.

При кинематическом исследовании зубчатого механизма разбиваем исследуемый механизм на составные части, т.е. выделим эпициклическое соединение колес и соединение зубчатых колес с неподвижной осью. Данный механизм имеет следующее строение:

Дифференциальный механизм, в состав которого входят центральные колеса 1, 3, сателлит 2, водило Н.

Рядовое соединение колес, которое образуют колеса 4,5,6.

Для выделенных соединений колес запишем формулы кинематических соотношений.

По условию задачи

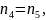
Тогда

Тогда

Подставив числовые значения, получим:

Значение передаточного числа, полученного графическим путем:

Погрешность между расчетным значением передаточного числа и значением, полученным графическим путем составляет:

Заключение

В ходе выполнения курсового проекта был проведен кинематический анализ механизма двигателя и определены линейные и угловые перемещения, скорости и ускорения характерных точек механизма.

В результате кинетостатического анализа были получены значения реакций кинематических парах и уравновешивающей силы для двух положений механизма.