Содержание

Y

Введение 4

1 Структурный анализ механизма 5

2 Кинематический анализ механизма 7

3. Силовой расчет механизма 12

4 Расчет замкнутого эпициклического механизма 19

Заключение 21

Список использованных источников 22

Введение

Курсовой проект выполняется в учебных целях по заданию кафедры “Механика”. В курсовом проекте проводится кинематический, кинетостатический анализ механизма, а также выполняется расчет замкнутого эпициклического механизма.

1 Структурный анализ механизма

Рисунок 1 – Структурная схема механизма

В рассматриваемом механизме семь кинематических пар с одной подвижностью (р₁=7), из которых 6 - вращательные и одна поступательная. Пар с двумя подвижностями в механизме нет (р₂=0).

Все звенья механизма совершают плоское движение, т. е. все его точки перемещаются параллельно одной неподвижной плоскости. Степень подвижности механизма (W) определяем по формуле Чебышева П.Л.

где n - число подвижных звеньев (n=5),

p₁ - число низших кинематических пар с одной подвижностью (p₁ =7).

Высших (с двумя подвижностями на плоскости) кинематических пар в механизме нет, p₂ =0.

Общее число степеней свободы механизма равно 1, т. е. для работы механизма достаточно одного ведущего звена, в качестве которого может быть использован кривошип АВ.

2 Кинематический анализ механизма

Последовательность кинематического расчета совпадает с последовательностью присоединения групп Ассура к исходному механизму. Вокруг точки А тонкой или пунктирной линией проводим окружность - траекторию движения оси пальца кривошипа. Проведя через точку С касательную к полученной окружности, определим крайнее положение кулисы. Для данной схемы механизма крайнее левое положение кулисы принято за нулевое. Остальные построения легко определяются на чертеже.

Определим исходные данные для анализа механизма.

Угловая скорость исходного звена:

Скорость точки В звена 2:

Ускорение точки В звена 2:

Выбираем масштабные коэффициенты.

Масштабный коэффициент плана механизма:

Масштабный коэффициент плана скорости:

Где – длина вектора скорости точки В на чертеже, мм,

Масштабный коэффициент плана ускорений:

Где - длина вектора ускорения точки В на чертеже, мм.

Построение планов скоростей.

Планы скоростей строим для 2 положений механизма (положения 3 и 9, рабочий и холостой ход соответственно).

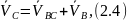
где 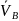– вектор абсолютной скорости точки В;

– вектор скорости точки В звена 3 относительно точки С, перпендикулярен звену 3;

– вектор скорости точки С кулисы 4. Направление совпадает с прямой, перпендикулярной звену 4;

– вектор скорости точки K конца кулисы. Эта скорость относится к скорости соотношением:

V_K/V_С = DK/DC.

– вектор абсолютной скорости точки E, движение вместе с главным ползуном по направлению совпадает с прямой, параллельной оси главного ползуна;

– вектор скорости точки К звена 5 относительно точки Е, перпендикулярен звену 5.

Проводим расчет скоростей звеньев механизма. Результаты расчета внесены в таблицу 1.

Таблица 1 – Величины скоростей звеньев

№ п-п	VВC, м/c	VC, м/с	VК, м/с	VКE, м/с	VЕ, м/с	VS3, м/c	VS5, м/c	ω3, об/с	ω4, об/с	ω5, об/с
3	0,26	1,3	1,8	0,12	1,81	1,3	1,8	0,96	5,1	1,26
9	0,13	1,4	1,9	0,11	1,9	1,3	1,9	0,48	5,4	1,15

Определяем значения угловых скоростей звеньев.

Угловая скорость звеньев механизма определяется по выражению:

Где - длина вектора скорости звена с плана скорости, мм,

- масштабный коэффициент для плана скорости,

- длина звена, м.

Результаты построений планов скоростей сводим в таблицу.

Для положения механизма 3:

Для положения механизма 9:

Построение планов ускорений.

План ускорений построен по векторным равенствам:

Где - абсолютное ускорение звена 3,

– нормальное ускорение звена 3;

- тангенциальное ускорение звена 3,

– нормальное ускорение точки С звена 4;

- тангенциальное ускорение точки С звена 4.

- абсолютное ускорение точки K звена 4, определяется по соотношению длин участков DC и DK,

А_K = (DK/DC)∙А_C.

– нормальное ускорение звена 5;

- тангенциальное ускорение звена 5,

- ускорение главного ползуна 6, направлено параллельно линии движения ползуна 6.

Величина нормальных ускорений звеньев определяется по формуле

Где - угловая скорость звена, с^-1,

- длина звена, м.

Таблица 2 - Расчет ускорений звеньев механизма

№
3	0,25	13,3	13,4	6,5	3,3	7,6	11,1	0,15	11,1	11,1	0,26	14,2	5,5	5,3
9	0,06	42,3	42,3	7,9	24,7	26,8	38,9	0,12	10,1	10,2	36	11,5	5,8	37,2

Величину угловых ускорений звеньев определяем по формуле

(2.10)

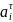– касательное ускорение звена, м/с^-2,

- длина звена, м.

Для положения механизма 3:

Для положения механизма 9: