Функция обратной пропорциональности.
1) Построение графиков функции обратной пропорциональности, содержащих переменную под знаком модуля.
Для построения графиков функции обратной пропорциональности, содержащих переменную под знаком модуля, рассмотрим несколько случаев:
а)
:
строим
и отображаем часть графика расположенную
ниже оси Ох, вверх, относительно оси Ох.
Пример 1: построить график функции
.
Построение:
,
график – гипербола 1-ой и 3-ей четвертей.
Пример 2: построить график функции
.
Построение:
,
график - гипербола 1-ой и 3-ей четвертей,
смещенная по оси Оу вниз на 3 единицы.
Пример 3: построить график функции
.
Построение:
график - гипербола 1-ой и 3-ей четвертей,
смещенная по оси Оу вверх на 1 единицу,
и по оси Ох вправо на 2 единицы.
б)
:
строим
и
отображают относительно оси Оу часть
графика, которая лежит правее оси Оу и
удаляют левую часть.
Пример 4: построить график
функции
.
Построение: , график – гипербола 1-ой и 3-ей четвертей.
Пример 5: построить график
функции
Построение: строим график функции и сдвигаем его вниз по оси Оу на две единицы.
Пример 6: построить график
функции
Построение: строим график функции
и отображаем правую часть графика
относительно оси Оу, а левую часть
графика убираем.
в)
:
строим график функции
и отображаем часть графика расположенную
ниже оси Ох, вверх, относительно оси Ох.
Пример 7: построить график
функции
.
Построение: строим график функции
,
и отображаем часть графика расположенную
ниже ос Ох вверх.
Пример 8: построить график
функции
Построение:
Пример 8: построить график
функции
Построение:
1)
2)
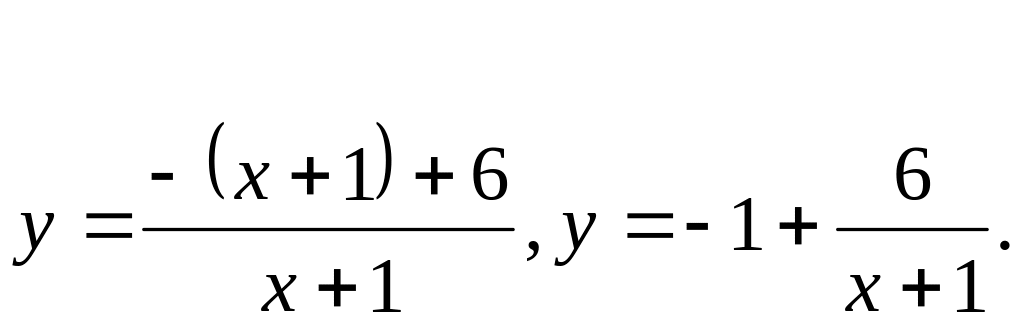
2) Решение дробно - рациональных уравнений, содержащих переменную под знаком модуля.
Решение этих уравнений сводится к
решению уравнений вида
Данное уравнение равносильно системе:
Пример 1: решить уравнение
.
Решение:
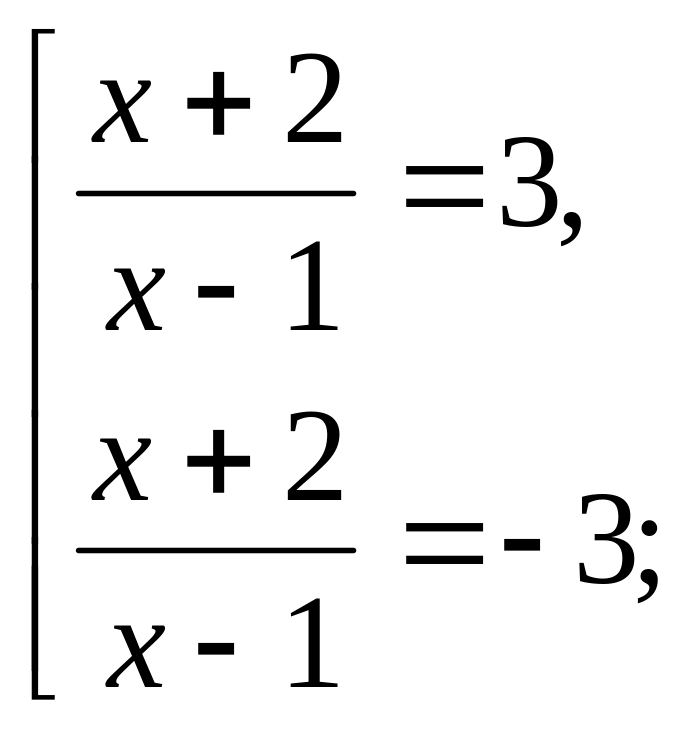
Ответ: 0,25; 2,5.
Пример 2: решить уравнение
Решение:
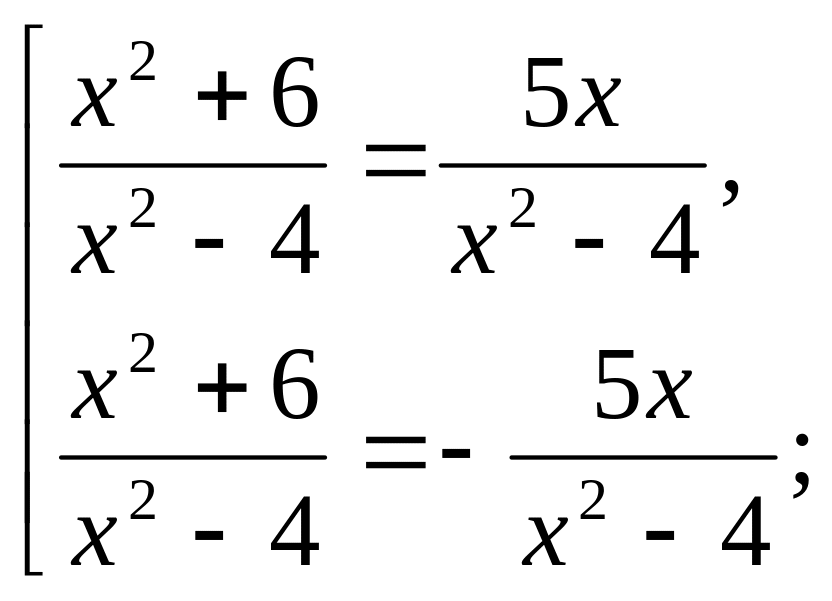
Ответ: -6; -1: 3.
Пример 3: решить уравнение
Решение: Пусть
;
Ответ: -5; -1.
Пример 4: решить уравнение
Решение:
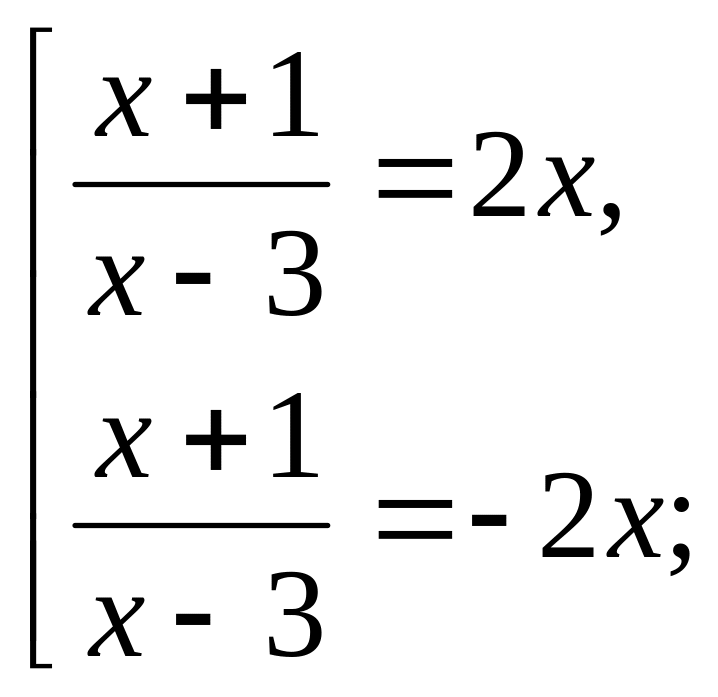
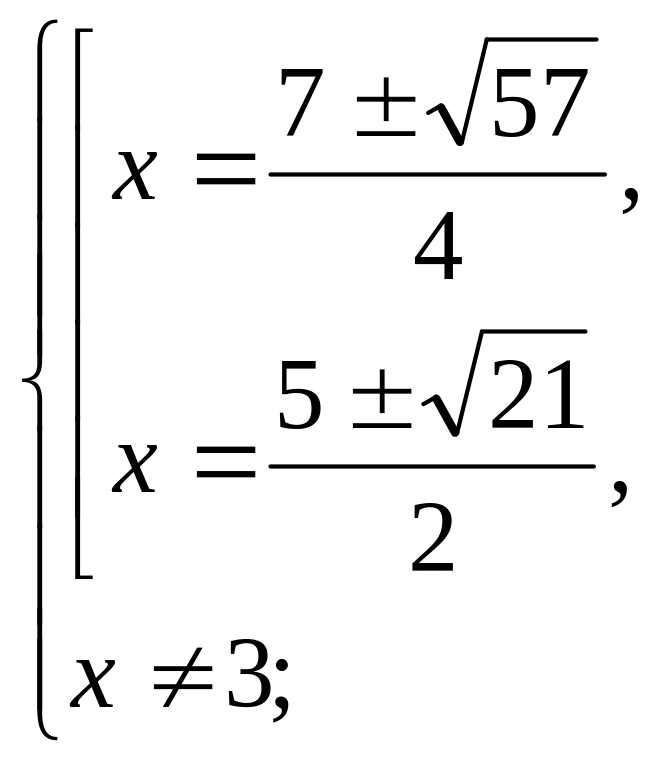
Ответ:
;
.
Пример 5: решить уравнение
Решение:
Ответ:
Пример 6: решить уравнение
Решение:
Ответ: 0; 2.
3)Решение дробно-рациональных неравенств, содержащих переменную под знаком модуля.
Эти неравенства, после раскрытия модулей,
сводятся к решению неравенств вида
или
которые
решаются методом интервалов.
Пример 1: решить неравенство
Решение:
Ответ:
Пример 2: решить неравенство
Решение:
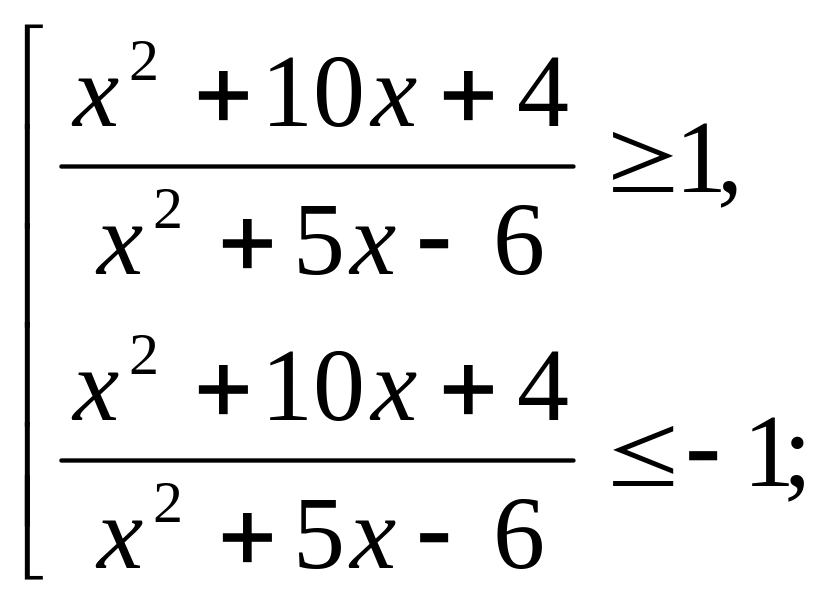
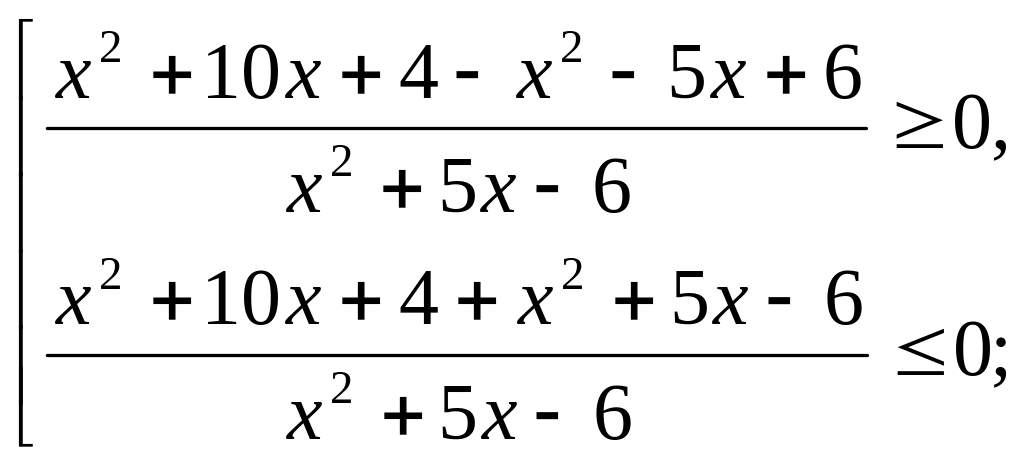
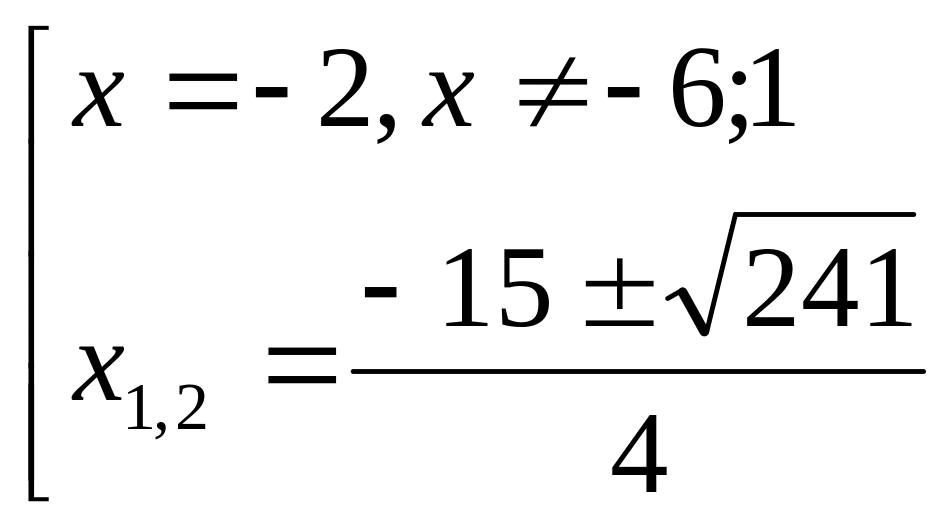
Ответ:
Пример 3: решить неравенство
Решение:
или
Ответ:
Пример 4: решить неравенство
Решение:
то
1)
2)
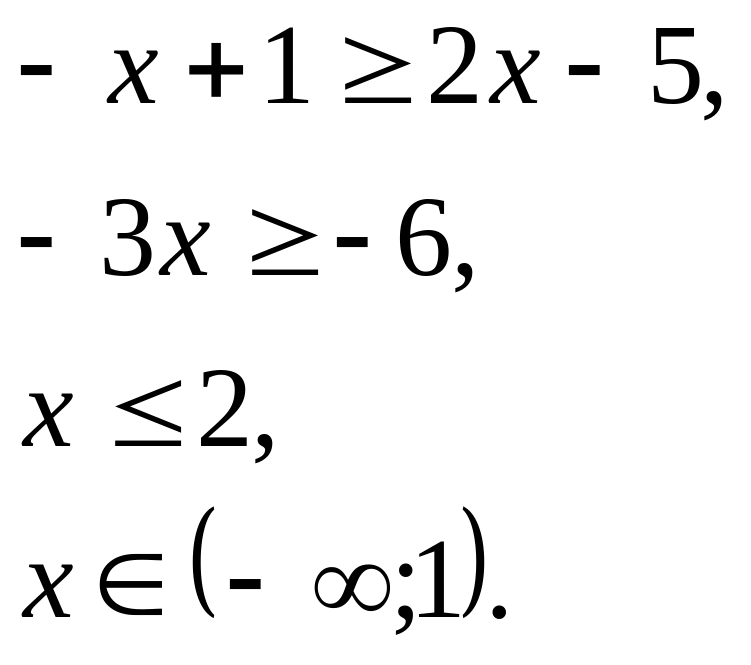
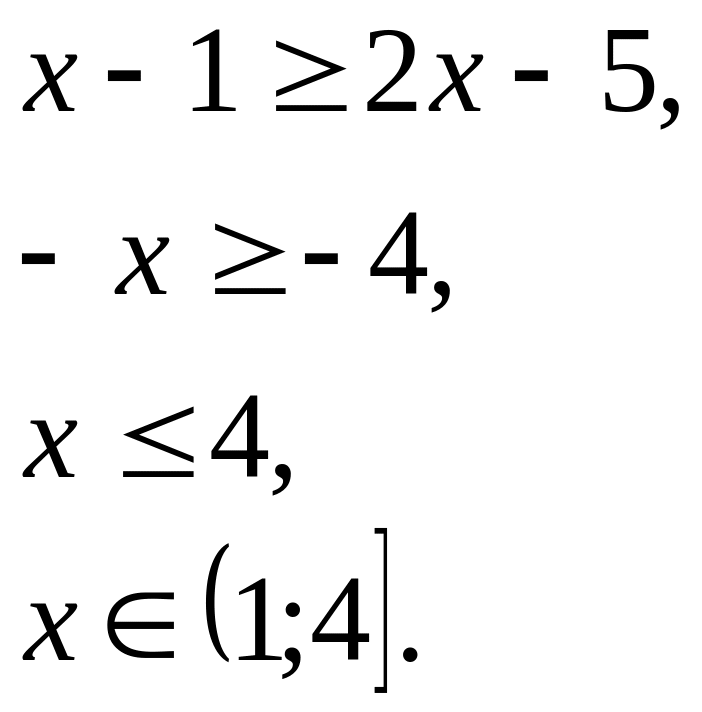
Ответ:
Пример 5: решить неравенство
Решение:
Решим методом интервалов: 1)
2)
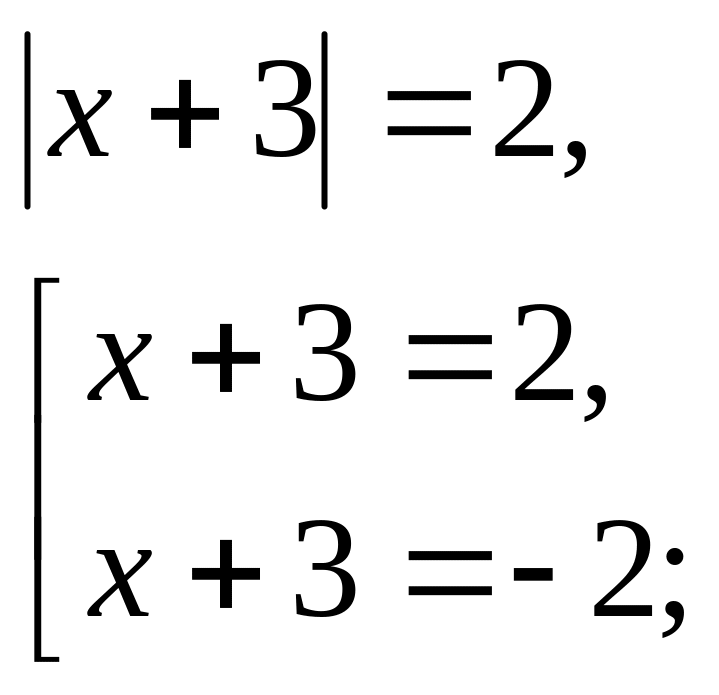
Ответ:
Пример 6: решить неравенство
Решение:
1)
2)
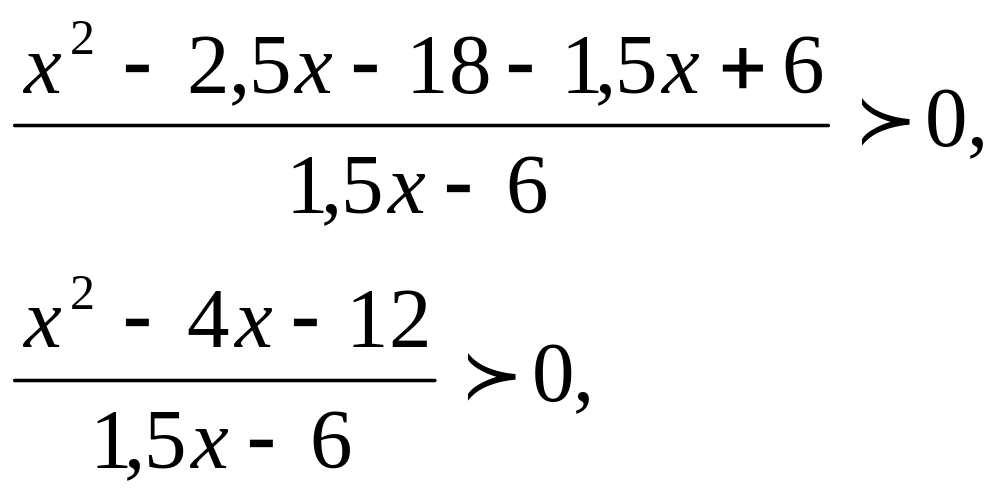
Ответ:
