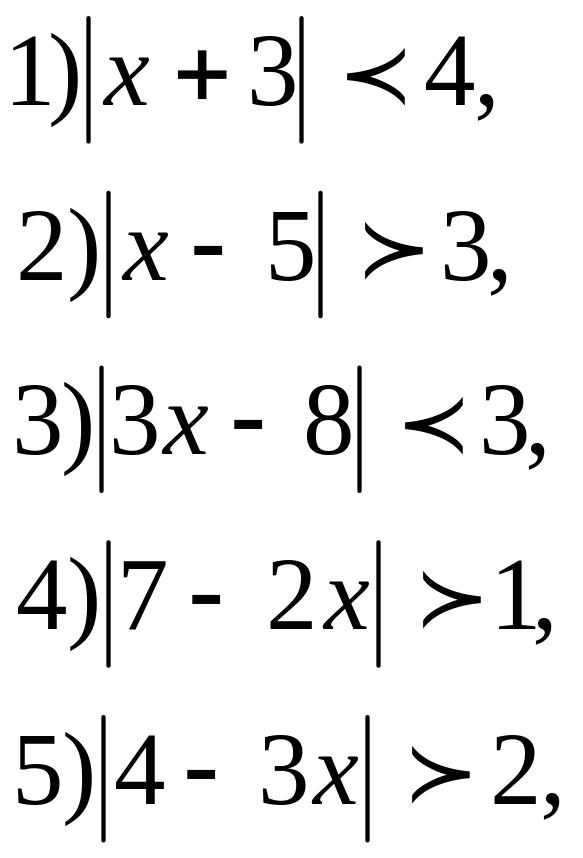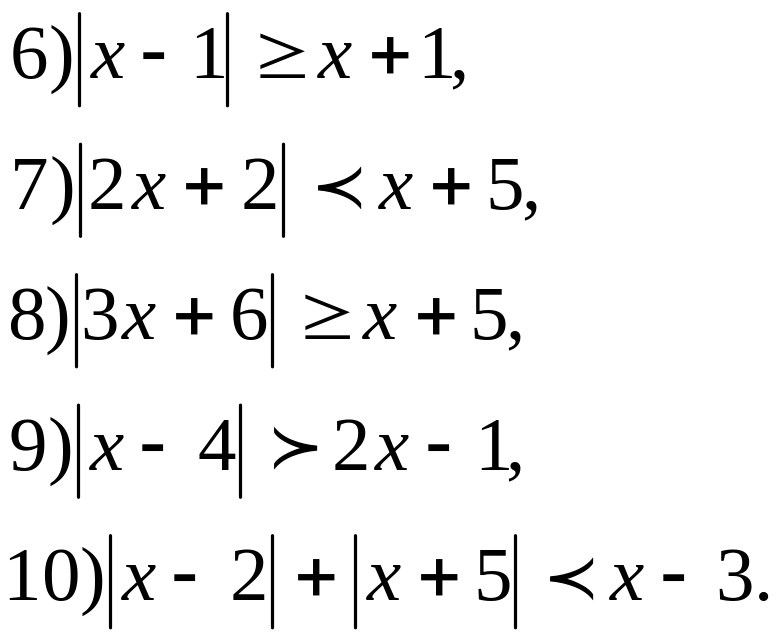- •Построение графиков функций, решение уравнений и неравенств, содержащих переменную под знаком модуля
- •1. Введение
- •Алгоритм построения графиков функций, содержащих модули.
- •Алгоритм решения уравнений, содержащих модули.
- •Алгоритм решения неравенств, содержащих модули.
- •Линейная функция
- •1) Построение графиков линейной функции, содержащих переменную под знаком модуля.
- •2) Решение линейных уравнений, содержащих переменную под знаком
- •3)Решение линейных неравенств, содержащих переменную под знаком
- •4 ) Задания для самостоятельной работы.
- •5) Зачетные задания по теме: «Линейная функция».
- •Квадратичная функция
- •1) Построение графиков квадратичной функции, содержащих
- •2) Решение квадратных уравнений, содержащих переменную под знаком
- •3)Решение квадратных неравенств, содержащих переменную под знаком
- •4) Задания для самостоятельной работы.
- •5) Зачетные задания по теме: «Квадратичная функция».
- •Функция обратной пропорциональности.
- •1) Построение графиков функции обратной пропорциональности, содержащих переменную под знаком модуля.
- •2) Решение дробно - рациональных уравнений, содержащих переменную под знаком модуля.
- •3)Решение дробно-рациональных неравенств, содержащих переменную под знаком модуля.
- •4) Задания для самостоятельной работы.
- •5) Зачетные задания по теме: «Функция обратной пропорциональности».
- •Итоговый зачет по курсу «Построение графиков функций, решение уравнений и неравенств, содержащих переменную под знаком модуля».
2) Решение линейных уравнений, содержащих переменную под знаком
модуля.
Эти уравнения, после раскрытия модулей сводятся к решению простых линейных уравнений вида кх+в=0, для которых возможны случаи:
а)
![]() тогда
тогда
![]() - единственный корень;
- единственный корень;
б)
![]()
![]() ,
то
,
то
![]() - корней нет;
- корней нет;
в)
![]() ,
,
![]() ,
то
,
то
![]() - бесконечное множество корней.
- бесконечное множество корней.
Пример 1: решить уравнение
![]()
Решение:
![]()
![]()
![]()
Ответ:
![]()
Пример 2: решить уравнение
![]()
Решение:
![]()
![]()
![]()
![]()
Ответ:
Пример 3: решить уравнение
![]()
Решение:
![]()
![]()
Ответ:
![]()
Пример 4: решить уравнение
![]()
Решение:
![]()
![]()
1)
![]() :
:
![]() ,
,
![]() ,
верно
,
верно
![]() ;
;
2)
![]() :
:
![]() ,
,
![]()
3)
![]() :
:
![]() ,
,
![]() .
.
Ответ:
![]() .
.
![]()
3)Решение линейных неравенств, содержащих переменную под знаком
модуля.
 Эти неравенства, после раскрытия
модулей, сводятся к решению неравенств
вида
Эти неравенства, после раскрытия
модулей, сводятся к решению неравенств
вида
![]() ,
( или
,
( или
![]() ),
где
),
где
![]() -
числа.
-
числа.
1)
,
то неравенство принимает вид
![]()
![]() и возможны случаи:
и возможны случаи:
а)
![]()
![]()
![]() ,
(или решений нет);
,
(или решений нет);
в)
![]() решений нет, (или
решений нет, (или
![]() ).
).
2)
![]() ,
то возможны случаи:
,
то возможны случаи:
а)
![]()
![]() ,
(или
,
(или
![]() );
);
в)
![]()
![]() ,
(или
,
(или
![]() .
.
Пример 1: решить неравенство
![]()
Решение: ,
![]()
![]() ,
,
![]() .
.
Ответ:
![]()
Пример 2: решить неравенство
![]()
Решение: ,
![]()
![]()
![]()
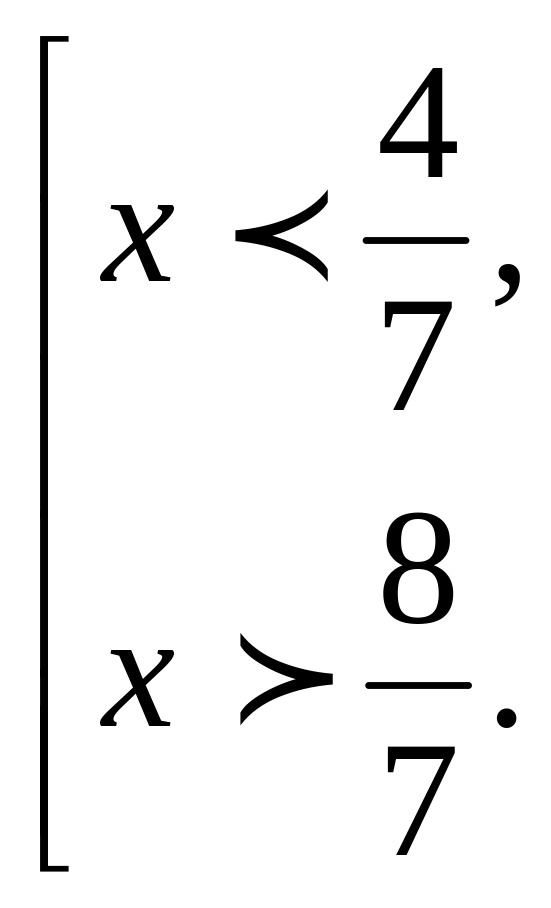
Ответ:
![]()
Пример 3: решить неравенство
![]()
Решение:
![]()
1)
![]() :
:
![]()
![]()
![]()
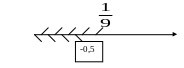
2)
![]() :
:
![]()
![]()
![]() .
.

![]()
Ответ:
![]() .
.
Пример 4: решить неравенство
![]()
Решение: ,
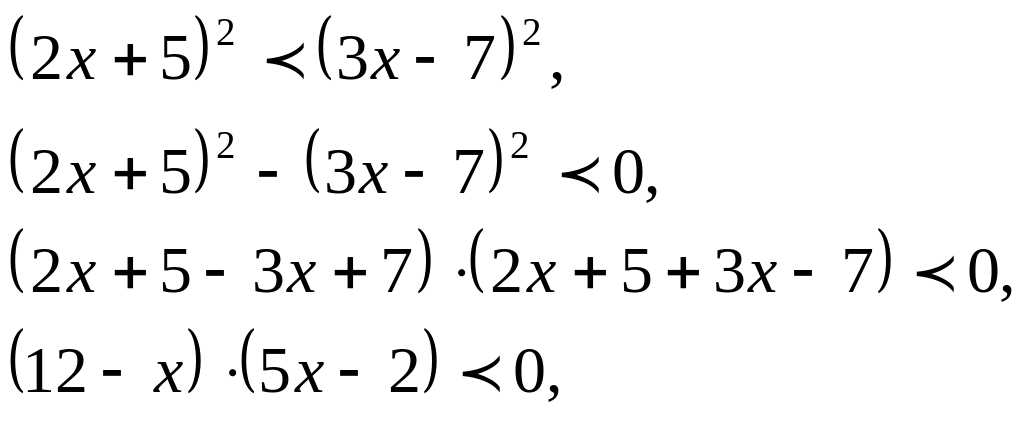
решим методом интервалов,
![]()
![]()
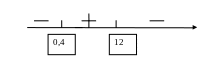
![]() .
.
Ответ:
![]() .
.
Пример 5: решить неравенство
![]()
Решение: ,
![]()
![]()
1)
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2)
![]() :
:
![]()
![]()
![]()
![]()
3)
![]() :
:
![]()
![]()
![]() .
.
Ответ:
![]()
4 ) Задания для самостоятельной работы.
1. Построить графики функций:
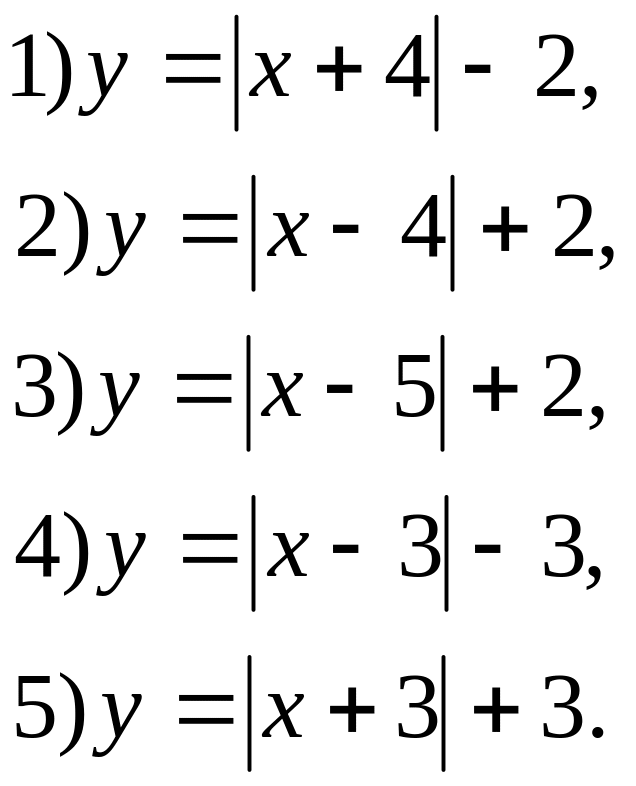
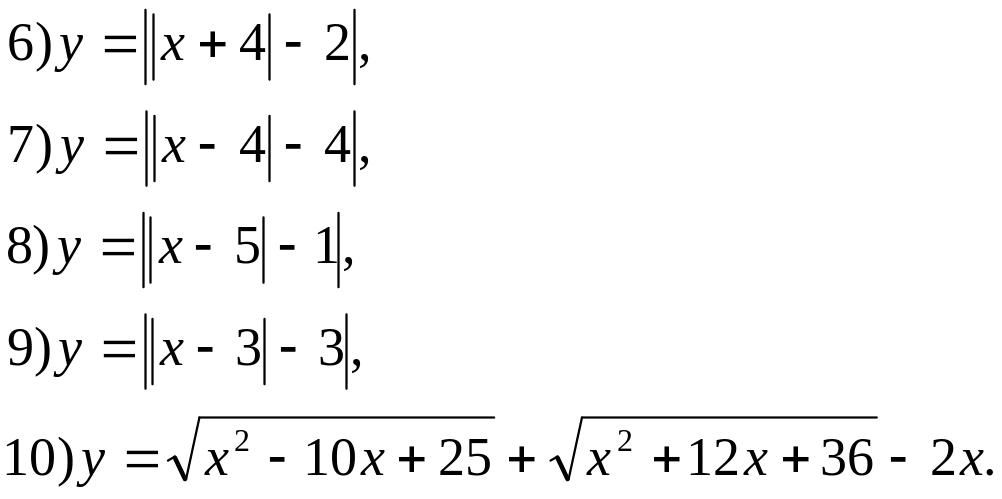
2. Решите уравнения:
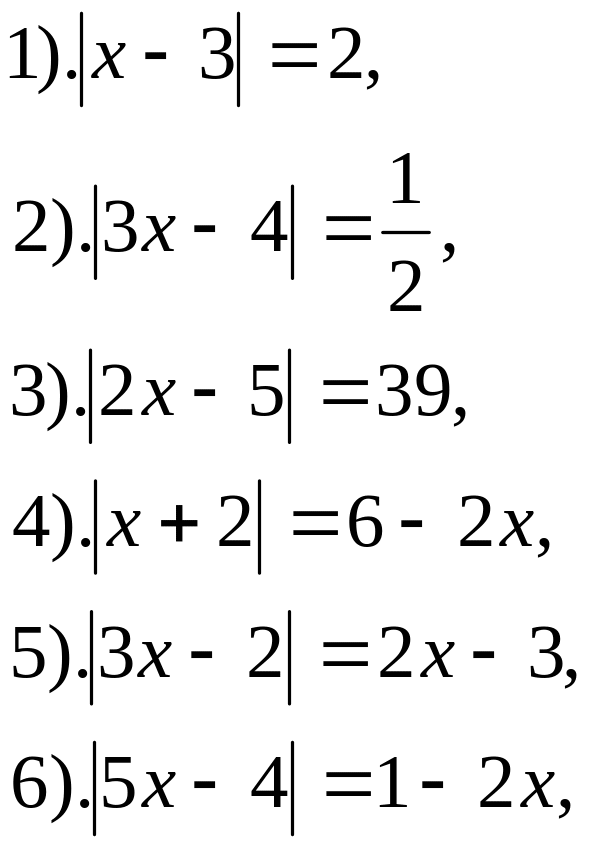
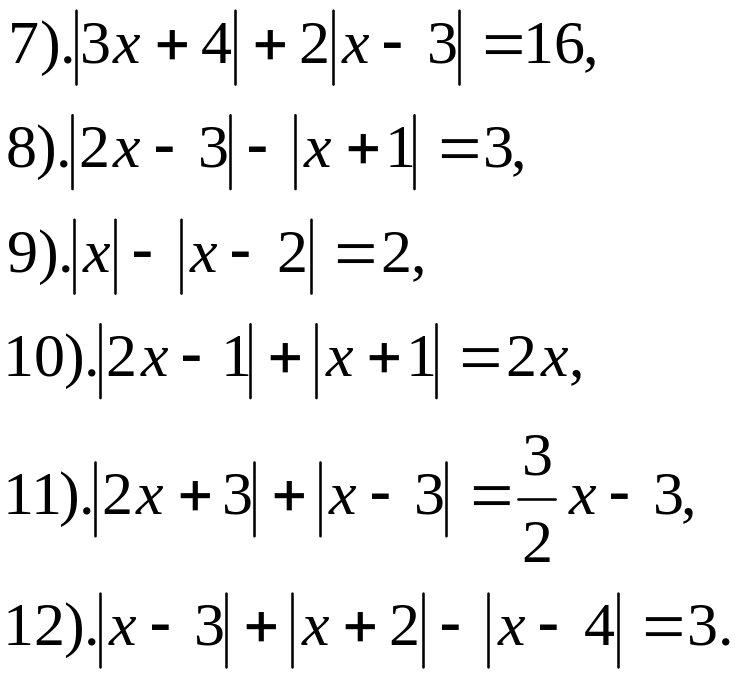
3. Решите неравенства