Алгоритм решения неравенств, содержащих модули.

Рассмотрим несколько видов неравенств, содержащих модули :

1. 

1) а  0 неравенство не имеет решений;

2) а = 0 первое неравенство не имеет решений, а второе: ;

3) а  0 неравенство равносильно системе неравенств:

,

2. 

1) а  0 решением неравенства является любое действительное число;

2) а = 0, решением неравенства является любое действительное число, кроме (или любое действительное число);

3) а  0 неравенство равносильно совокупности неравенств:

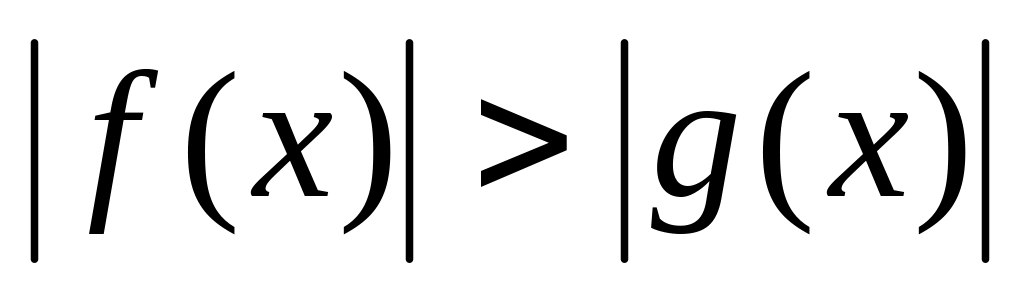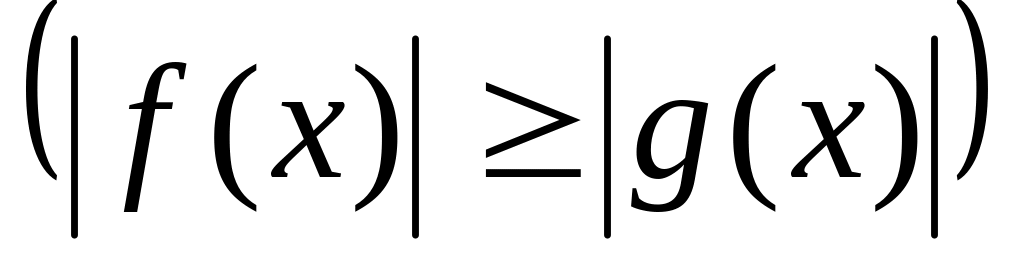3. , или , .

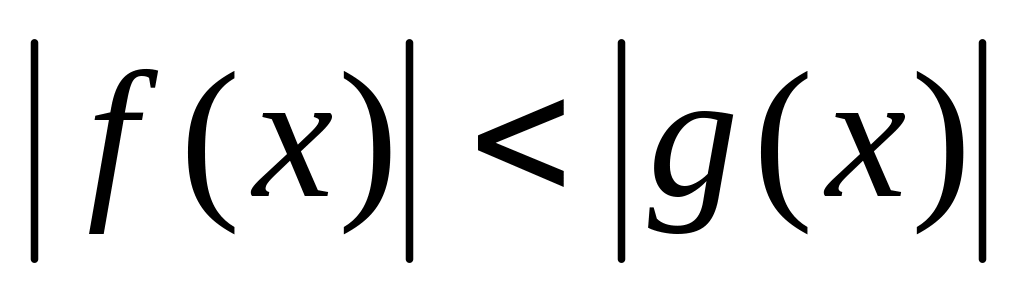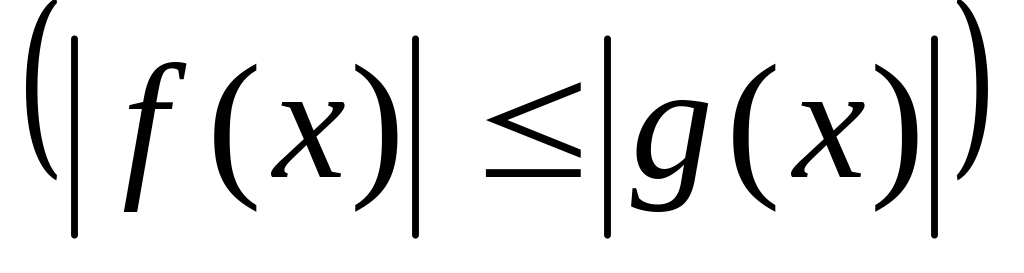1) возвести обе части неравенства в квадрат: ;

2) разложить разность квадратов на множители: ;

3) решить полученное неравенство методом интервалов.

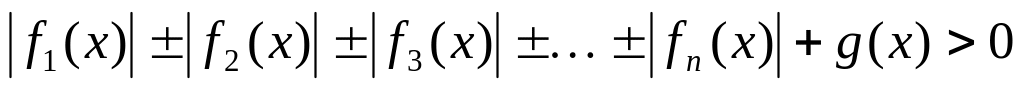4. или 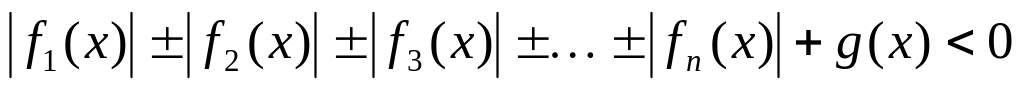, решают методом разбиения на промежутки:

1) находят значения переменной, при которых входящие в неравенство модули равны нулю (нули модулей);

2) область определения неравенства разбивают этими значениями на промежутки и по определению модуля, определяют знаки модуля на полученных промежутках;

3) на каждом из полученных промежутков раскрывают модули и получают неравенство:

4) решают каждое неравенство;

5) полученные решения сравнить с данным промежутком и вывести общее решение;

6) объединить решения, полученные на всех промежутках.

Линейная функция

1) Построение графиков линейной функции, содержащих переменную под знаком модуля.

Для построения графиков линейной функции, содержащих переменную под знаком модуля, рассмотрим несколько случаев:

а) : строим и отображаем часть графика расположенную ниже оси Ох, вверх, относительно оси Ох.

Пример 1: построить график функции

Построение:

х	0	2
у	– 4	0

Пример 2: построить график функции

Построение:

х	0	2
у	5	– 1

б) построение графиков с помощью разбиения на промежутки.

Пример 3: построить график функции

Построение: х – 4 = 0 х + 2 = 0

х = 4 х = – 2

1) : у = – х + 4 – х – 2, у = – 2х + 2.

2) : у = – х + 4 + х + 2, у = 6.

3) : у = х – 4 + х + 2, у = 2х – 2

Пример 4: построить график функции

Построение:

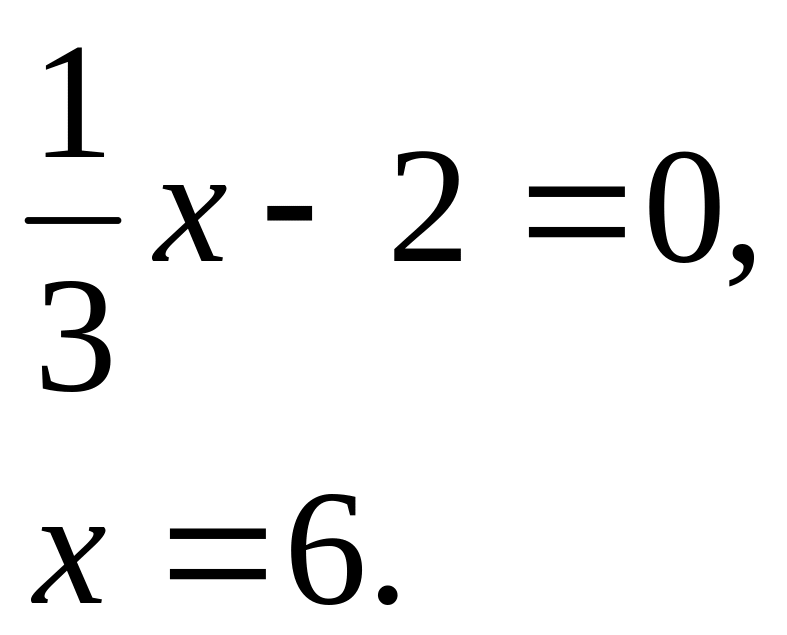
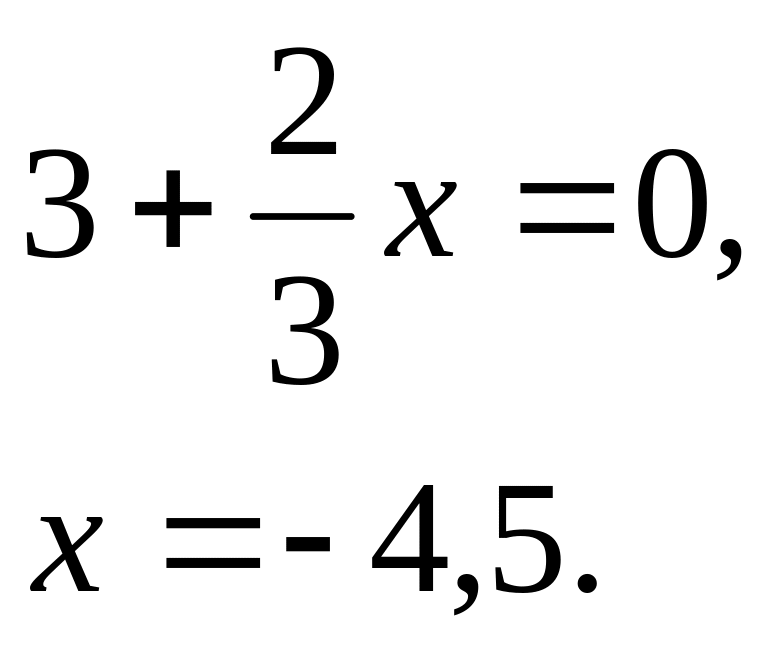
1) : ;

2) :

3) : .

Пример 5: построить график функции

Построение:

1) : ;

2) : ;

3) : , .

в) построение графиков с двойными модулями.

Пример 6: построить график функции

Построение: 1) строим график функции ;

2) построенный график опускаем на 2 единицы вниз;

3) отображаем часть графика расположенного ниже оси Ох, вверх относительно оси Ох.