
- •Построение графиков функций, решение уравнений и неравенств, содержащих переменную под знаком модуля
- •1. Введение
- •Алгоритм построения графиков функций, содержащих модули.
- •Алгоритм решения уравнений, содержащих модули.
- •Алгоритм решения неравенств, содержащих модули.
- •Линейная функция
- •1) Построение графиков линейной функции, содержащих переменную под знаком модуля.
- •2) Решение линейных уравнений, содержащих переменную под знаком
- •3)Решение линейных неравенств, содержащих переменную под знаком
- •4 ) Задания для самостоятельной работы.
- •5) Зачетные задания по теме: «Линейная функция».
- •Квадратичная функция
- •1) Построение графиков квадратичной функции, содержащих
- •2) Решение квадратных уравнений, содержащих переменную под знаком
- •3)Решение квадратных неравенств, содержащих переменную под знаком
- •4) Задания для самостоятельной работы.
- •5) Зачетные задания по теме: «Квадратичная функция».
- •Функция обратной пропорциональности.
- •1) Построение графиков функции обратной пропорциональности, содержащих переменную под знаком модуля.
- •2) Решение дробно - рациональных уравнений, содержащих переменную под знаком модуля.
- •3)Решение дробно-рациональных неравенств, содержащих переменную под знаком модуля.
- •4) Задания для самостоятельной работы.
- •5) Зачетные задания по теме: «Функция обратной пропорциональности».
- •Итоговый зачет по курсу «Построение графиков функций, решение уравнений и неравенств, содержащих переменную под знаком модуля».
Построение графиков функций, решение уравнений и неравенств, содержащих переменную под знаком модуля
СОДЕРЖАНИЕ |
|
1. Введение. |
3 |
2. Линейная функция: |
5 |
1) построение графиков линейной функции; |
5 |
2) решение уравнений; |
9 |
3) решение неравенств; |
10 |
4) задания для самостоятельной работы. |
12 |
5) зачетные задания по теме: «Линейная функция». |
13 |
3. Квадратичная функция: |
15 |
1) построение графиков квадратичной функции; |
15 |
2) решение квадратных уравнений; |
18 |
3) решение квадратных неравенств; |
20 |
4) задания для самостоятельной работы. |
23 |
5) зачетные задания по теме: «Квадратичная функция». |
25 |
4. Функция обратной пропорциональности: |
27 |
1) построение графиков обратной пропорциональности; |
27 |
2) решение дробно-рациональных уравнений; |
31 |
3) решение дробно-рациональных неравенств; |
33 |
4) задания для самостоятельной работы. |
35 |
5) зачетные задания по теме: «Функция обратной пропорциональности" |
37 |
5. Итоговый зачет по курсу «Построение графиков функций, решение уравнений и неравенств, содержащих переменную под знаком модуля». |
39 |
1. Введение
Тема «Решение уравнений и неравенств, содержащих переменную под знаком модуля и построение графиков функций, содержащих модули» осталось вне поля зрения программного материала общеобразовательного курса средней школы. Однако во время сдачи экзаменов в форме ЕГЭ и во время сдачи вступительных экзаменов в высшие учебные заведения наши учащиеся постоянно встречаются с уравнениями и неравенствами, содержащих переменную под знаком модуля. Возникла необходимость введения этой темы через факультативные занятия и элективные курсы в предпрофильных и профильных классах. Работая, много лет, я пришла к системе, по которой занимаюсь с 8-9 класса. В программу элективных курсов 9 класса входят три раздела: линейная функция, квадратичная функция и функция обратной пропорциональности.
Алгоритм построения графиков функций, содержащих модули.
 :
:
1) строят график функции ,
2) отображают относительно оси Ох часть графика, которая лежит ниже оси Ох.
1) строят график функции
![]() ;
;
2) отображают относительно оси Оу часть графика, которая лежит правее оси Оу и удаляют левую часть.
Алгоритм решения уравнений, содержащих модули.
Рассмотрим несколько видов уравнений
с модулями и их решение (где
![]() и
и
![]() функции переменной х, а – заданное
действительное число).
функции переменной х, а – заданное
действительное число).
1) а 0, уравнение не имеет решения;
2) а = 0, уравнение равносильно уравнению
![]() ;
;
3) а 0, уравнение
равносильно совокупности уравнений:![]()
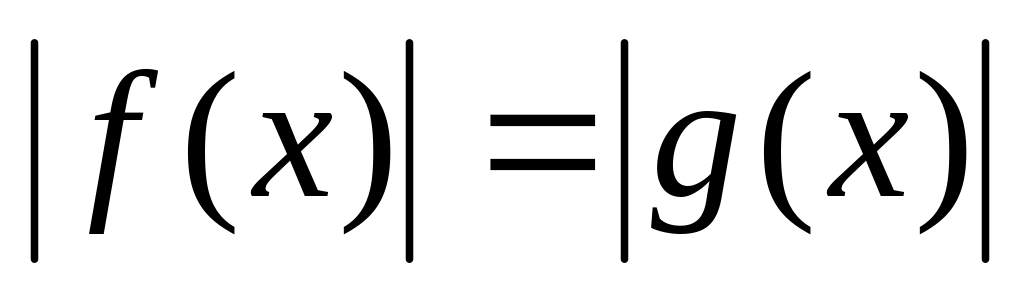 ,
уравнение равносильно совокупности
уравнений:
,
уравнение равносильно совокупности
уравнений: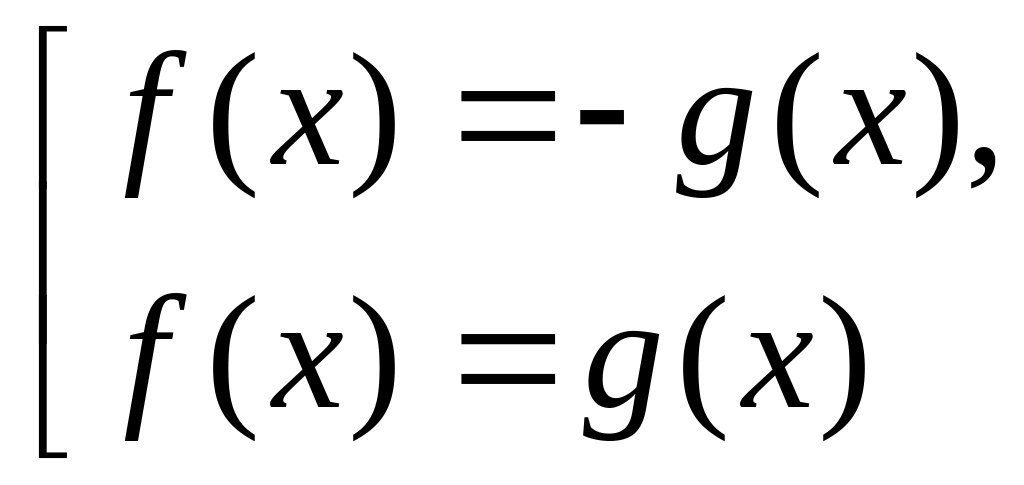
3.
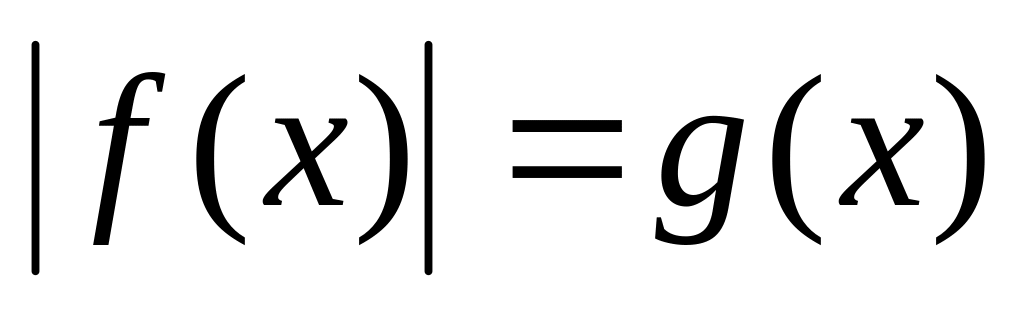 ,
уравнение равносильно совокупности
уравнений:
,
уравнение равносильно совокупности
уравнений: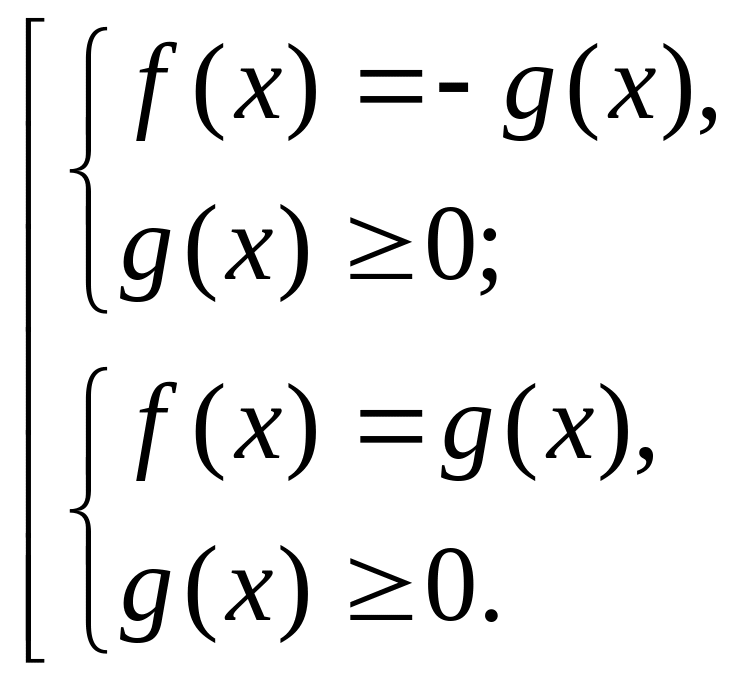
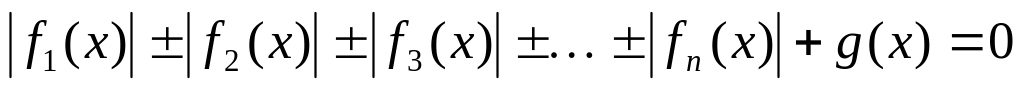 ,
решают методом разбиения на промежутки:
,
решают методом разбиения на промежутки:
1) находят значения переменной, при которых входящие в уравнение модули равны нулю (нули модулей);
2) область определения уравнения разбивают этими значениями на промежутки и по определению модуля, определяют знаки модуля на полученных промежутках;
3) на каждом из полученных промежутков раскрывают модули и получают уравнение:
![]()
4) решают каждое уравнение;
5) проверяют принадлежность корней данному промежутку(если корень принадлежит промежутку, то является корнем, в противном случае – посторонний корень).
