
- •Магнит өрісі және оның сипаттамалары. Магнит индукция векторы.
- •Вектор және скаляр түріндегі Био-Савар-Лаплас заңы. Магнит өрісінің суперпозиция принципі. - векторлық түрде жазылған Био – Савар – Лаплас заңы,
- •Ампер заңы. Параллель токтардың өзара әсерлесуі.
- •Лоренц күші. Магнит өрісіндегі зарядталған бөлшектің қозғалысы.
- •Магнит өрісі үшін толық ток заңы.
- •Магнит ағыны. Магнит өрісі үшін Гаусс теоремасы.
- •Магнит өрісіндегі тогы бар өткізгіштің орын ауыстыруы кезіндегі істелінетін жұмыс.
- •Фарадейдің электромагниттік индукция заңы. Ленц ережесі.
- •Контурдың индуктивтілігі. Өздік индукция.
- •Өзара индукция.
- •Магнит өрісі энергиясы. Магнит өрісі энергиясының көлемдік тығыздығы.
- •Магнетиктер. Заттардағы магнит өрісі үшін толық ток заңы.
- •Электромагниттік өріс үшін Максвелл теңдеуілері. Максвелдің бірінші теңдеуі Фарадей ашқан электромагниттік индукцияның негізгі заңы бойынша эқк: , (3.1)
- •3.2 Максвелдің екінші теңдеуі
- •3.3 Максвелл теңдеулерінің толық жүйесі
- •Электромагниттік толқындар және олардың қасиеттері.
- •Электромагниттік толқындардың дифракциясы
- •Электромагниттік өріс үшін толқындық теңдеу.
- •Электромагниттік толқын энергиясы. Электромагниттік энергия ағынының тығыздығы. Умов-Пойнтинг векторы.
- •Электрлік тербелмелі контурдағы еркін тербелістің дифференциалдық теңдеуі. Томсон формуласы.
- •Электрлік тербелмелі контурдағы еркін өшетін тербелістің дифференциалдық теңдеуі. Өшудің логарифмдік декременті.
- •Мәжбүр электромагниттік тербелістің дифференциалдық теңдеуі. Резонанс.
- •Айнымалы ток. Айнымалы ток үшін Ом заңы.
- •Айнымалы токтың қуаты.
- •Геометриялық оптиканың негізгі заңдары.
- •Шағылу және сыну заңдары. Толық ішкі шағылу.
- •Линзалар және оның негізгі сипаттамалары. Жұқа линзаның формуласы.
- •Жинағыш және шашыратқыш линзалардағы нәрсенің кескінін тұрғызу.
- •Фотометрлік шамалар және олардың өлшем бірліктері. Жарықталыну заңы.
- •Жарық толқындарының интерференциясы. Оптикалық жол айырымы мен фазалар айырымы арасындағы байланыс. Интерференциялық максимум және минимум шарттары.
- •Екі когерентті көздерінен алынған жарық интерференция. Интерференциялық жолақтың ені.
- •Бірдей қалыңдықты жолақтар. Ньютон сақинасы.
- •Жарық дифракциясы. Гюйгенс-Френель принципі.
- •Френельдің зоналар әдісі.
- •Дөңгелек дискідегі және дөңгелек саңлаудағы Френель дифракциясы.
- •Бір саңлаудағы Фраунгофер дифракциясы.
- •Дифракциялық тор.
- •Нормаль (қалыпты) және аномаль (қалыпсыз) жарық дисперсиясы. Жарық дисперсиясының электрондық теориясы.
- •Жарықтың жұтылуы. Бугер-Ламберт заңы.
- •Табиғи және поляризацияланған жарық. Малюс заңы.
- •Шағылу және сыну кезіндегі жарық поляризациясы. Брюстер заңы.
- •Қосарланып сыну кезіндегі жарық поляризициясы. Николь призмасы.
- •Оптикалық актив заттағы жарықтың поляризация жазықтығының бұрылуы.
- •Жылулық сәулеленудің негізгі сипаттамалары. Абсолют қара дене. Кирхгоф заңы.
- •Абсолют қара дене үшін Стефан-Больцман заңы.
- •Абсолют қара дене үшін Вин заңдары.
- •Вин және Релей-Джинс формулалары. Ультракүлгін апаты.
- •Кванттық гипотеза. Планк формуласы.
- •Фотондар. Жарық кванттарының энергиясы және импульсі.
- •Сыртқы фотоэффект заңдары. Эйншт*ейн теңдеуі.
- •Комптон эффекті.
- •Бөлшектер қасиеттерінің корпускулалы-толқындық дуализмі. Де Бройль гипотезасы.
- •Де Бройль толқыны. Де Бройль толқынының қасиеттері.
- •Альфа-бөлшектерінің шашырауымен жүргізілген Резерфорд тәжірибесі. Атомның планетарлық моделі.
- •Сутегі атомының сызықтық спектрі. Жалпыланған Бальмер формуласы.
- •Бор постулаттары. Франк және Герц тәжірибелері.
- •Бор бойынша сутегі атомының спектрі. Электронның толық энергиясы.
- •Гейзенбергтің анықталмаушылық қатынастары.
- •Микробөлшектердің толқындық қасиеттері. Толқындық функция және оның статистикалық мағынасы.
- •Шредингердің уақыттық және стационарлық теңдеулері.
- •Бірөлшемді тікбұрышты шұңқырдағы бөлшек.
- •Бөлшектің тікбұрышты потенциалдық тосқауыл арқылы өтуі.
- •Кванттық механикадағы сызықтық гармоникалық осциллятор.
- •Сутегі атомы үшін Шредингер теңдеуі.
- •Кванттық сандар. Паули принципі.
- •Атом ядросының құрылысы.
- •Ядроның массалық ақауы. Ядроның байланыс энергиясы. Меншікті байланыс энергиясы.
- •Ядролық күштер. Күштердің алмасу сипаты. Ядро моделі.
- •Радиоактивтік ыдырау заңы. Нуклид активтілігі.
- •Альфа-ыдырау мен бета-ыдырау кезіндегі ығысу ережелері.
- •Альфа- бета- және гамма-сәулелерін шығарудың табиғаты және заңдылықтары
- •Ядролық реакциялар.
Магнетиктер. Заттардағы магнит өрісі үшін толық ток заңы.
Магнетиктер деп магниттік қасиеттері қарастырылатын кез-келген денелерді айтады. Магнетиктер магнит өрісін қоздыруға не өзгертуге қабілетті.Магнетиктерді сыртқы магнит өрісіне енгізгенде магнетиктердің магниттелуі өз кезегінде осы өрісті өзгертеді. Әртүрлі магнетиктердің қасиеттерін, олардың магнит өрісінің индукциясының шамасына әсерін түсіндіру үшін, магнит өрісінің заттардың атомдары мен молекулаларына әсерін зерттеу қажет.
Біртекті
ортадағы магнит өрісі индукциясының
вакуумдегі магнит өрісі индукциясынан
шамасы бойынша қанша есе өзгеше екендігін
көрсететін физикалық шаманы ортаның
магниттік өтімділігі деп атайды:![]()
Затардың магниттік қасиеттері олардың құрамына кіретін атомдардың немесе элементар бөлшектердің (электрондар, протондар және нейтрондар) магниттік қасиеттерімен анықталады. Қазіргі кезде протондар мен нейтрондардың магниттік қасиеттері электрондардың магниттік қасиеттерінен 1000 еседей әлсіз екендігі анықталған.Электрондардың маңызды қасиеттерінің бірі оларда электр өрісімен қатар, меншікті магнит өрісінің болуы. Электронның меншікті магнит өрісін спиндік (spin – айналу) деп атайды. Электрон магнит өрісін, сонымен қатар, ядроның айналасындағы орбитальдық қозғалысы нәтижесінде (дөңгелек микроток деп қарастыруға болады) тудырады.
Электромагниттік өріс үшін Максвелл теңдеуілері. Максвелдің бірінші теңдеуі Фарадей ашқан электромагниттік индукцияның негізгі заңы бойынша эқк: , (3.1)
мұндағы
Фm
–
магнит индукциясының ағыны. Ол өз кезінде
төмендегідей формула бойынша
анықталады: ,(3.2)
,(3.2)
мұндағы
S – тұйық контурдың ауданы; Вn
– магнит индукциясы векторы В-ның
ауданға нормаль
 -ге
проекциясы. Тұрақты ток бөлімінде
келтірілген анықтама бойынша тұйық
контурдағы ЭҚК:
-ге
проекциясы. Тұрақты ток бөлімінде
келтірілген анықтама бойынша тұйық
контурдағы ЭҚК: ,(3.3)мұндағы
,(3.3)мұндағы
 электр
өрісі кернеулік векторының
электр
өрісі кернеулік векторының
 контур элементі
контур элементі
 бағытына проекциясы. Келтірілген
(3.1) және (3.3) теңдеулердің оң жақтарын
өзара теңестіретін болсақ, онда (3.2)
ескере отырып алатынымыз:
бағытына проекциясы. Келтірілген
(3.1) және (3.3) теңдеулердің оң жақтарын
өзара теңестіретін болсақ, онда (3.2)
ескере отырып алатынымыз: .
(3.4)
.
(3.4) –
дербес
туынды магнит индукциясының ағынының
тек уақытқа тәуелділігін көрсетеді.Алынған
(3.4) соңғы теңдеуден магнит өрісінің
өзгерісі, айнымалы электр өрісінің
пайда болуының себепшісі екені байқалады.
Кернеулік векторының циркуляциясы
нөлден өзгеше, демек бұл магнит өрісі
қоздырған электр өрісі, потенциалды
өріс емес, құйынды өріс екендігін
дәлелдейді. Құйынды өрістің күш сызықтары
тұйық және олардың кеңістікте өткізгіштің
бар-жоғына байланыссыз-ақ пайда
болатындығын көрсетеді. Аталған (3.4)
теңдігінің негізінде Максвелл осындай
қортындыға келді. Сондықтан (3.4) өрнегі
Максвелдің интегралдық түрдегі бірінші
теңдеуі деп аталады.
–
дербес
туынды магнит индукциясының ағынының
тек уақытқа тәуелділігін көрсетеді.Алынған
(3.4) соңғы теңдеуден магнит өрісінің
өзгерісі, айнымалы электр өрісінің
пайда болуының себепшісі екені байқалады.
Кернеулік векторының циркуляциясы
нөлден өзгеше, демек бұл магнит өрісі
қоздырған электр өрісі, потенциалды
өріс емес, құйынды өріс екендігін
дәлелдейді. Құйынды өрістің күш сызықтары
тұйық және олардың кеңістікте өткізгіштің
бар-жоғына байланыссыз-ақ пайда
болатындығын көрсетеді. Аталған (3.4)
теңдігінің негізінде Максвелл осындай
қортындыға келді. Сондықтан (3.4) өрнегі
Максвелдің интегралдық түрдегі бірінші
теңдеуі деп аталады.
3.2 Максвелдің екінші теңдеуі
(3.4)
өрнегін және де көптеген тәжірибе
көрсеткіштерін талдай отырып, Максвелл
кері құбылыстың болуы ықтимал деген
қорытындыға келді. Яғни, оның болжауынша,
айнымалы электр өрісінің күш сызықтары
тұйықталған магнит өрісін туғызуға
тиіс.Максвелдің бұл болжамының дұрыстығына
төмендегідей тәжірибе арқылы көз
жеткізуге болады. Құрамында конденсаторы
бар айнымалы ток тізбегін қарастырайық.
Тығыздығы
 өткізгіштік ток тізбек бөліктерінде
магнит өрісін туғызады. Бұл
тізбекте қозғалыстағы зарядтардан
пайда болған өткізгіштік ток жалғаушы
сымдардан жүреді де конденсатордың
астарындағы саңылауда (аралықта) ток
болмайды. Бірақ, бұл уақыт мезеттерінде
конденсатор зарядталып және разрядталып
тұрғандықтан астарладың арасында
айнымалы электр өрісі болады. Бұл өріс
әрбір уақыт мезеттерінде өткізгіштердегі
ток өткендегідей, әрі оған тең ток
өткендей магнит өрісін тудырады. Айнымалы
электр өрісі мен одан пайда болған
магнит өрісінің арасындағы өзара
мөлшерлік байланысты анықтау үшін
Максвелл ығысу тогы деген ұғым енгізді.
Токтар сияқты кеңістікте магнит өрісін
тудырғандықтан айнымалы электр өрісін
Максвелл ығысу тогы деп атады. Ал
өткізгіштік тогы мен ығысу тогы тең
болуы керек, яғни
өткізгіштік ток тізбек бөліктерінде
магнит өрісін туғызады. Бұл
тізбекте қозғалыстағы зарядтардан
пайда болған өткізгіштік ток жалғаушы
сымдардан жүреді де конденсатордың
астарындағы саңылауда (аралықта) ток
болмайды. Бірақ, бұл уақыт мезеттерінде
конденсатор зарядталып және разрядталып
тұрғандықтан астарладың арасында
айнымалы электр өрісі болады. Бұл өріс
әрбір уақыт мезеттерінде өткізгіштердегі
ток өткендегідей, әрі оған тең ток
өткендей магнит өрісін тудырады. Айнымалы
электр өрісі мен одан пайда болған
магнит өрісінің арасындағы өзара
мөлшерлік байланысты анықтау үшін
Максвелл ығысу тогы деген ұғым енгізді.
Токтар сияқты кеңістікте магнит өрісін
тудырғандықтан айнымалы электр өрісін
Максвелл ығысу тогы деп атады. Ал
өткізгіштік тогы мен ығысу тогы тең
болуы керек, яғни
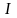 өт
өт ығ
,
онда олардың тығыздықтары да өзара тең
болады деп алуымыз керек
өт
ығ
,
онда олардың тығыздықтары да өзара тең
болады деп алуымыз керек
өт ығ.
ығ.
Конденсатордың
астарына жақын жердегі өткізгіштік
токтың тығыздығы
өт
 ,
(3.5)
,
(3.5)
мұндағы –зарядтың
беттік тығыздығы,
–зарядтың
беттік тығыздығы,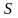 –конденсатор
астарларының
ауданы. Олай болса
өт
–конденсатор
астарларының
ауданы. Олай болса
өт .Электр
өрісін электр ығысу
.Электр
өрісін электр ығысу
 векторымен сипаттауға болады.
Электростатикадан конденсатордың
астарындағы зарядтың беттік тығыздығы
электр ығысуымен
векторымен сипаттауға болады.
Электростатикадан конденсатордың
астарындағы зарядтың беттік тығыздығы
электр ығысуымен
 байланысты екені белгілі:
байланысты екені белгілі: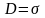 осыны
ескерсек, онда ығысу тогының тығыздығы
ығ
осыны
ескерсек, онда ығысу тогының тығыздығы
ығ .
(3.6) Дербес туынды белгісі, магнит өрісі
тек электр ығысуының уақыт бойынша
өзгеру жылдамдығымен анықталатынын
көрсетеді. Мұндағы
.
(3.6) Дербес туынды белгісі, магнит өрісі
тек электр ығысуының уақыт бойынша
өзгеру жылдамдығымен анықталатынын
көрсетеді. Мұндағы
 ығ
және
өт
векторларының бағыттары әрқашан
ығ
және
өт
векторларының бағыттары әрқашан
 векторымен бағыттас болатынын көрсетуге
болады, сондықтан (3.6) теңдігін векторлық
түрде жазуға болады:
ығ
векторымен бағыттас болатынын көрсетуге
болады, сондықтан (3.6) теңдігін векторлық
түрде жазуға болады:
ығ .
(3.7) Өткізгіштік және ығысу токтарын
сәйкесінше былай көрсетейік
өт
өт
.
(3.7) Өткізгіштік және ығысу токтарын
сәйкесінше былай көрсетейік
өт
өт
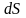 және
ығ
ығ
.
Магнит
өрістерін есептегенде толық токты алу
қажет
және
ығ
ығ
.
Магнит
өрістерін есептегенде толық токты алу
қажет
 өт
өт ығ
ығ (
өт
(
өт ығ)
ығ) (
өт+
(
өт+ )
(3.8)
)
(3.8)
Енді
 ығ
ығ
екенін
ескеріп, мұндағы
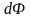 ығ–
электрлік
ығысу
векторының
бет арқылы өтетін элементар ағыны, онда:
ығ–
электрлік
ығысу
векторының
бет арқылы өтетін элементар ағыны, онда:
ығ .3.9)
.3.9)
Ығысу
тогы және толық ток түсінігі айнымалы
ток тізбегінің әрқашанда тұйық екендігін
айқындайды: өткізгішітік ток өткізгіштің
ұштарында үзіліп қалады, ал диэлектриктерде
және вакуумда өткізгіштердің ұштарын
ығысу тогы өткізгіштік тогын жалғайды.
Егер толық токты мына түрде жазсақ:
өт
ығ
= (
өт
ығ
)
,
(3.10)
(
өт
ығ
)
,
(3.10)
онда
магнит өрісі кернеулігінің циркуляциясы
туралы теореманы былай жазамыз: өт
ығ
өт
+
(3.11)
өт
ығ
өт
+
(3.11)
немесе
өткізгіштік тогының және ығысу тоғының
тығыздығы арқылы векторлық түрде
төмендегідей көрсетуге болады: өт
өт ығ
)
ығ
) .
(3.12)
.
(3.12)
Бұл Максвелдің екінші теңдеуі электр өрісінің қандай өзгерісі болмасын, ол құйынды магнит өрісін тудыратынын тағайындайды. Өткізгіштік тогы жоқ болғанда немесе бұл токты ескермеуге болатын кезде (мысалға кондесатордың астарларының арасында) толық ток заңын былай жазуға болады
ығ
 .
.
