1. Магнит өрісі және оның сипаттамалары. Магнит индукция векторы.

Тогы бар өткізгіштер бір-біріне тікелей емес, оларды қоршаған магнит өрістері арқылы әсер етеді. Магнит өрісінің көзі болып қозғалыстағы электр зарядтары табылады. Сондай-ақ, тұрақты магниттердің магнит өрісін (Ампер гипотезасы) зат молекулаларының ішінде айналып жүрген электрлік микротоктар туғызады. Магнит өрісінің электр өрісінен айырмашылығы, ол тек қозғалыстағы зарядтарға (токтарға) ғана әсер етеді.

Магнит өрісін сипаттау үшін өрістің күштік сипаттамасы 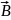магнит индукциясы векторын енгізу қажет. векторының бағыты ретінде магнит өрісінде еркін бағдарланатын магнит тілшесінің S оңтүстік полюстен N солтүстік полюске қарай бағыты алынады. Электростатикадағы күш сызықтары сияқты, магнит индукциясы сызықтарын жүргізуге болады. Магнит индукциясы сызықтары (магнит өрісінің күш сызықтары) деп әр нүктесіне жүргізілген жанаманың бағыты векторымен бағыттас сызықтарды айтады. Тұрақты магнит пен тогы бар катушканың магнит өрістерінің күш сызықтары 1.1- суретте келтірілген.

Магнит өрісінің күш сызықтары тұйықталған болады, себебі, магниттік зарядтар деген магнит өрісінің көзі жоқ. Мұндай қасиетке ие, күштік өрістерді құйынды деп атайды. Тәжірибе, тогы бар өткізгішке магнит өрісі тарапынын күш әсер ететіндігін көрсетеді. Зерттеліп отырған магнит өрісіне тогы бар өткізгішті енгізіп, өткізгіштің жекелеген элементар бөліктеріне әсер ететін күшті өлшеу арқылы магнит өрісін сапалық сипаттауға болады.

2. Вектор және скаляр түріндегі Био-Савар-Лаплас заңы. Магнит өрісінің суперпозиция принципі. - векторлық түрде жазылған Био – Савар – Лаплас заңы,

- скалярлық түрде жазылған Био – Савар – Лаплас заңы. мұндағы:   - магнит тұрақтысы.Магнит өрісін сипаттау үшін индукция векторымен қатар магнит өрісінің кернеулік векторы енгізілген. Магнит өрісінің кернеулігі ортаның қасиеттеріне байланыссыз, ол магнит өрісін туғызатын токтың шамасына тікелей байланысты болады.Кернеулік векторының өлшем бірлігі                                                     Магнит өрісінің кернеулік векторы арқылы жазылған Био – Савар – Лаплас заңы:векторлық түрі -    скаляр түрі -   Вакуумдегі магнит өрісінің индукция векторы мен кернеулік векторы арасындағы байланыс  келесі түрде жазылады:

. Магнит индукциясы векторының модулі келесі өрнекпен анықталады: (1.8) мұндағы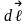– мен арасындағы бұрыш.

(1.8) өрнегі Био-Савар-Лаплас заңының скалярлық түрі. Магнит өрісі үшін суперпозиция принципі орындалады: берілген нүктедегі бірнеше токтардың тудыратын магнит өрісінің қорытқы индукция векторы осы нүктедегі әрбір ток тудыратын өрістердің магнит индукцияларының векторлық қосындысына тең: .

3. Био-Савар-Лаплас заңы және оны тогы бар дөнгелек өткізгіштің центріндегі магнит өрісін есептеу үшін қолдану.

Дөңгелек токтың центріндегі магнит өрісінің индукциясы: .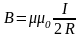

4. Био-Савар-Лаплас заңы және оны түзу токтың магнит өрісін есептеу үшін қолдану.

Био-Савар-Лаплас заңын пайдаланып тогы бар шексіз ұзын түзу өткізгіштің төңірегіндегі магнит өрісінің индукциясын анықтауға болады. Тогы бар шексіз ұзын түзу өткізгіштің центрінен өткізгішке перпендикуляр R қашықтықтағы нүктедегі магнит индукциясы: