Глава 2. Дифракция в поликристаллах

Для рентгеновских лучей, электронов и нейтронов, длины волн которых соизмеримы с межатомными расстояниями, то есть лежат в диапазоне от 0.5 до 3.0 Å, кристаллы служат трехмерными дифракционными решетками.

Пусть на цепочку одинаковых атомов с межатомным расстоянием (периодом трансляции) а падает под углом ₀ плоская волна. Каждый атом становится источником сферической рассеянной волны. Расстояние между атомами на несколько порядков меньше, чем расстояние от источника падающего излучения до цепочки атомов и от рассеивающих атомов до регистрирующего устройства (пленка или счетчик). Поэтому фронты падающих и рассеянных волн можно рассматривать как плоские.

Разность хода лучей, рассеянных соседними атомами, определяется как а·(cos - cos₀), и в направлениях, в которых она равна целому (h) числу длин волн , рассеянные волны при интерференции максимально усилят друг друга. В силу сферичности рассеянных атомами волн максимумы возникнут по всем образующим дифракционного конуса с углом раствора 2.

Из формулы

а·(cos - cos₀) = h (1)

следует, что каждому целому значению числа h, удовлетворяющему условию h  /2а, будет соответствовать свой дифракционный конус.

Если рассеивает атомная плоскость, то ее можно рассматривать как совокупность двух пересекающихся атомных цепочек с периодами трансляций а и b, каждая из которых дает свою систему дифракционных конусов. Интенсивность будет максимальной в тех направлениях, где дифракционные конусы пересекаются попарно, т.е. выполняются условия:

а·(cos - cos₀) = h (2)

b·(cos - cos₀) = k

Трехмерная периодическая решетка кристалла полностью определяется тремя атомными цепочками, параллельными координатным осям. В этом случае можно записать три соотношения:

а·(cos - cos₀) = h

b·(cos - cos₀) = k (3)

c·(cos - cos₀) = l,

где а, b, с – периоды решетки по трем некомпланарным направлениям, принятым за оси координат; h, k, l – целые числа, равные 0, 1, 2,… . Углы, составляемые дифрагированным и падающим лучами с осями координат, обозначены как , ,  и ₀, ₀, ₀ соответственно.

Соотношения (1), (2), (3) представляют собой условия Лауэ для одно-, двух- и трехмерной решеток соответственно.

Каждое из трех условий (3) определяет семейство конусов, для осей (x, y, z). Одновременное выполнение всех трех условий (3) при заданных индексах h, k, l означает, что для появления дифракционного максимума три конуса должны пересечься по одному направлению. Ясно, что в общем случае такое пересечение не имеет места (рис. 5), поскольку растворы конусов, определяемые периодами а, b, с, независимы друг от друга и пересекаются лишь попарно. Встает вопрос о том, как в этом случае получить дифракционную картину?

Рис. 5. Дифракционные конусы при рассеянии на трехмерной решетке.

В уравнениях Лауэ (3) величины а, b, являются фундамениальными характеристиками для определенного кристалла и не меняются в процессе его исследований. Углы ₀, ₀, ₀ определяют направление падающих лучей, и их можно точно задать, равно как и фиксировать величину длины волны  падающего излучения. Поэтому на первый взгляд кажется, что в трех условиях Лауэ остается только три неизвестных величины, определяющих направление рассеянных лучей: ,  и , которые можно найти совместным решением уравнений. Однако это не так. На самом деле неизвестные , ,  не независимы. Для случая, когда пространственная решетка может быть описана прямоугольной системой координат, углы , ,  связаны между собой известным тригонометрическим соотношением:

cos² + cos² + cos² = 1. (4)

Для косоугольных координатных осей

cos² + cos² + cos² = (5)

Таким образом, для нахождения трех неизвестных мы имеем уже 4 уравнения, которые в общем случае несовместны и общего решения не имеют. Это означает, что при произвольной взаимной ориентации падающих лучей и кристалла дифракцию можно и не наблюдать: три дифракционных конуса в общем случае не пересекаются по одной прямой. Чтобы одновременно могли пересечься по одной линии три дифракционных конуса, т.е. для получения дифракционного максимума, необходимо, не считая искомых углов , , , непрерывно изменять еще какую-либо из величин в условиях (3). Отсюда вытекают три основных метода получения дифракционной картины, используемых в структурном анализе:

1) метод Лауэ;

2) метод вращения монокристалла;

3) метод поликристалла или метод Дебая.

Для осуществления метода Лауэ монокристалл освещается полихроматическим пучком лучей, включающим некоторый интервал длин волн. В этом случае для ряда длин волн из этого интервала условия (3) и (4) или (5) будут выполняться одновременно, и мы получим четкую дифракционную картину.

При освещении монокристалла монохроматическим излучением для получения дифракционной картины необходимо непрерывно изменять углы ₀, ₀, ₀, что достигается вращением или колебанием монокристалла.

Наконец, последний метод наблюдения дифракции, метод Дебая, использует в отличие от 2-х первых не монокристаллический, а поликристаллический, т.е. состоящий из мелких (10^-3 см) монокристаллов (или кристаллитов) образец. Если в таком образце кристаллики ориентированы беспорядочно, то при освещении его параллельным пучком монохроматических рентгеновских лучей множество кристалликов окажется в положениях, удовлетворяющих условиям Лауэ (3), и возникнет дифракционная картина.

Дифракцию в поликристаллах проще всего объяснить, исходя из представлений, развитых Вульфом и Брэггами вскоре после открытия рентгеновских лучей. Они рассмотрели кристалл как совокупность (семейство) параллельных, расположенных на одинаковых расстояниях друг от друга, заполненных атомами плоскостей (так называемых плоских сеток). Таких семейств плоскостей в кристалле можно построить множество. Каждое семейство будет иметь свое межплоскостное расстояние d – кратчайшее расстояние между сетками, измеренное по направлению нормали, и свой символ (hkl), называемый индексами Миллера. Символ (hkl) (индексы Миллера) означает, что семейство параллельных плоскостей делит отрезок а на h частей, отрезок b на k частей, а отрезок с на l частей (рис. 6).

В качестве примера рассмотрим две решетки: ОЦК (объемно-центрированную кубическую) и ГЦК (гранецентрированную кубическую).

На одну ОЦК решетку приходится 2 атома с базисом 000, ½ ½ ½. Один из этих атомов располагается в вершине куба. Начало координат совпадает с координатами данного атома. В принципе, любой из 8 атомов, находящихся в вершине куба, может быть выбран за начальный. Каждый из 8 атомов, находящихся в такой позиции, является общим для 8 аналогичных ячеек, поэтому от каждого из атомов, находящихся в вершинах, на долю одной элементарной ячейки приходится 1/8 атома. Поскольку вершин 8, то получаем, что на одну элементарную ячейку атомов, расположенных в идентичных положениях – вершинах куба – приходится один, положение которого в дальнейшем и выбираем за начало координат. Второй атом с координатами ½ ½ ½ расположен в центре куба и принадлежит только одной элементарной ячейке.

На элементарную ячейку в ГЦК решетке приходится 4 атома. В данной решетке атомы занимают вершины куба, а также середины граней. Поскольку граней в кубе 6 и каждая является общей с соседней ячейкой, то на одну элементарную ячейку от атомов, находящихся в таких позициях, приходится 3 атома с координатами ½ ½ 0, ½ 0 ½ и 0 ½ ½ (рис. 7).

Через атомы мысленно можно провести прямые, т.е. атомные ряды. Ряды упаковываются в плоскости, которые определенным образом расположены в пространстве. Очевидно, что для двух рассматриваемых выше решеток базис различен, то и набор плоскостей будет различаться в случае ОЦК и ГЦК решеток.

Атомные плоскости в кристаллах обозначаются с помощью индексов Миллера (hkl). Плоскости, в отличие от координат атомов, выражаются целыми числами. Каждая плоскость отсекает по координатным осям некоторые отрезки s, p, q, меньшие 1. Тогда h = 1/s, k = 1/p, l = 1/q.

Р ис. 6. Определение символов Миллера (hkl): h = 1/s, k = 1/p, l = 1/q.

а)	б)

Рис. 7. Плоскости (110) и (111) в ОЦК (а) и ГЦК (б) решетках.

Для кристаллов некубических сингоний нахождение индексов Миллера представляет собой более сложную задачу, что связано с несимметричностью решетки, с различием размеров трансляций и углов. Эту задачу вы выполните с помощью формул, запрограммированных в программе Index.exe, находящейся в основной папке BASA.

Излучение, проникая в кристалл на некоторую глубину, отражается от системы параллельных плоских сеток по законам геометрической оптики. При достаточной величине кристалла (не менее 10^-5 см) в отражении примет участие очень большое число плоских сеток. Отраженные лучи, идущие по одному направлению, интерферируют между собой. Вследствие интерференции отраженный пучок будет обладать заметной интенсивностью только в том случае, если разность хода лучей, рассеянных двумя соседними плоскостями семейства, будет равна целому числу длин волн. Обозначим расстояние между плоскими сетками через d, а угол, составленный падающим лучом с плоской сеткой (угол скольжения), через θ. Разность хода  между лучами, рассеянными двумя ближайшими сетками, равна (см. рис. 8)  = ab + bc = 2dsinθ. Дифракционный максимум будет наблюдаться тогда, когда  равно целому числу длин волн, т. е. когда выполняется условие:

2dsinθ = nλ, (6)

где n = 1, 2, 3…- порядок отражения.

Рис. 8. К выводу условия Вульфа - Брэггов.

Формула (6) впервые была выведена крупнейшим русским кристаллографом Ю. В. Вульфом и англичанами отцом и сыном Брэггами. Формула Вульфа - Брэггов (6) лежит в основе дифракционных методов определения и анализа структуры кристаллов. С ее помощью можно рассчитать значения d/n = /2sinθ, так κак в случае характеристического излучения длина волны  известна заранее, а угол θ может быть определен экспериментально по дифракционной картине. В структурном анализе в формуле (6) n обычно принимают равным единице, так как отражение n-го порядка от семейства плоскостей с межплоскостным расстоянием d эквивалентно отражению первого порядка от семейства плоскостей с межплоскостным расстоянием d/n. Обозначают d/n = d_hkl, где (hkl) – индексы интерференционного максимума, равные индексам Миллера (hkl) n - го отражения.

Рассмотрим поликристалл, на который в направлении о-о падает пучок параллельных монохроматических лучей. В силу малости размеров составляющих поликристалл кристаллитов в облучаемом объеме их будет находиться множество: 10¹¹. Пусть в кристаллите (I) плоскости с межплоскостным расстоянием d₁ находятся в отражающем положении. Как видно на рис. 9, дифрагированный этим кристалликом луч будет составлять угол 2θ₁ с продолжением первичного пучка о-о. Если перпендикулярно направлению падающих лучей о-о поставить пленку, то на ней появится черная точка. Однако в образце найдутся и другие кристаллиты (например, I^'), в которых плоскости с тем же межплоскостным расстоянием d₁, составляя с осью о-о угол 2θ₁, также будут находиться в отражающем положении, но ввиду беспорядочной ориентации окажутся иначе развернутыми вокруг оси о-о. Дифрагированный кристалликом I' луч даст свою черную точку на пленке. В результате лучи, отраженные различным образом ориентированными вокруг оси о-о кристалликами, в которых плоскости с межплоскостным расстоянием d₁ находятся в отражающем положении, заполнят в пространстве поверхность конуса с у глом раствора 4θ₁, и на пленке, перпендикулярной о-о, возникнет кольцо.

Рис. 9. Рассеяние поликристаллом.

Кроме того, в поликристаллическом образце всегда есть кристаллики, которые также окажутся в отражающем положении, но в отражении будут участвовать плоские сетки другого семейства (другое значение d в уравнении (6)). Отраженные от таких кристалликов лучи образуют конус с другим углом раствора 4θ, и на пленке возникает второе кольцо.

В целом число дифракционных конусов и число колец на пленке зависит от числа различных по межплоскостным расстояниям систем атомных плоскостей, участвующих в отражении в различных кристалликах.

Если на пути дифракционных конусов перпендикулярно падающему пучку поставить фотопленку, то получим снимок в виде серии концентрических окружностей, расположенных вокруг центрального пятна, отвечающего месту пересечения пленки с падающим первичным пучком (рис. 10).

Рис. 10. Дифракционная картина от поликристалла, полученная на плоский экран.

Вместо плоского экрана, роль которого обычно выполняет рентгеновская пленка, в качестве детектора рассеянного излучения можно использовать сцинцилляционные счетчики.

Следует подчеркнуть, что вид основных уравнений дифракции: условий Лауэ (4) и закона Вульфа - Брэггов (6), а также принципы методов получения дифракционной картины не зависят от природы падающего на кристалл излучения (рентгеновские лучи, электроны или нейтроны). Любую дифракционную картину вещества можно охарактеризовать числом и взаимным расположением линий и их интенсивностью. Вид дифракционной картины определяется характером атомного расположения и индивидуален для каждого кристалла, поэтому значения межплоскостных расстояний d_hkl, рассчитанные по формуле (6), и относительные^* интенсивности отражений являются "паспортом" кристалла и позволяют однозначно идентифицировать исследуемое вещество. Используемая для этой цели картотека JCPDS составлена по результатам анализа рентгенограмм кристаллов, поскольку рентгенографический метод получения дифракционной картины является наиболее простым в реализации.

Зная межплоскостные расстояния, их индексы и тип кристаллической решетки, можно определить ее периоды. Для кубического кристалла все периоды одинаковы, т.е.

a = b = c = d(h²+k²+l²)^1/2 (7).

Формула (7) называется квадратичной формой. Для кристаллов некубических сингоний квадратичная форма имеет более сложный вид. Так, для тетрагональной сингонии

, (8)

а для гексагональной сингонии:

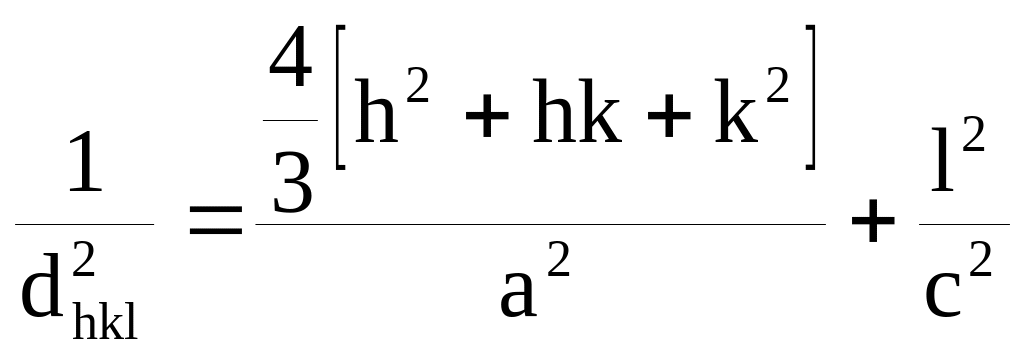. (9)

Это связано с тем, что трансляции по разным кристаллографическим направлениям различны, а углы между ними могут отличаться от 90°.

Определив тип кристаллической решетки, периоды a, b, c и углы α, β, γ, можно рассчитать объем V элементарной ячейки кристалла, а зная химический состав соединения и число атомов N, приходящихся на одну элементарную ячейку, оценить плотность исследуемого вещества по формуле:

ρ = N·m/V, (10)

где m – масса атома исследуемого вещества в граммах (m = A · а.е.м. = А·1.66·10^-24 г , где А – атомный вес вещества (по таблице Менделеева), а.е.м. – атомная единица массы), V = а³·10^-24 см³.

__________________

^* относительные интенсивности отражений: взятое в процентах отношение интенсивностей линий рентгенограммы к интенсивности самой сильной линии.