
Задача 6. Выбор варианта при равнозначности оценок
Классическая задача, которую в теории принятия решений называют задачей о Буридановом осле.
Дано: Ровно посередине между двумя совершенно одинаковыми копнами сена стоит осёл. Он не может выбрать, к какой из них нужно подойти, и, в конце концов, умирает от голода.
Цель: Какой алгоритм выбора надо применить для его спасения?
При решении данной задачи мы сталкиваемся с ситуацией многоальтернативного выбора без критериев, позволяющих оценить в момент принятия решения правильность сделанного выбора. Поведение в ситуациях выбора при отсутствии критериев для осуществления этого выбора стало предметом обсуждения в философских спорах с XIV века. Тогда же возник знаменитый анекдот об осле, который, якобы, должен сдохнуть от голода между двумя одинаковыми копнами сена в случае, если он находится на равном расстоянии от них, т.е. когда у него нет никаких оснований для предпочтения того или другого копна сена.
Для решения этой задачи можно применить алгоритм случайного выбора. Если стратегия, случайно приписанная случайному выбору, окажется неудачной -то от нее всегда можно будет отказаться. Но пока не работают критерии того, какой выбор надо делать, любой конкретный выбор априорно равно эффективен (потому ведь и делается случайный выбор), а значит, и ничем не хуже любого другого выбора. Иначе говоря, неважно какой выбор сделает осел, главное, чтобы выбор был сделан.
В рамках логики самой задачи можно, однако, показать, что рационально мыслящий осёл никогда не умрёт с голоду, хотя и нельзя сказать, какую копну сена он выберет. Отказ от еды можно тоже считать выбором. Таким образом, из трёх вариантов выбора (копна слева, копна справа и голодная смерть) третий вариант будет хуже всех, поэтому осёл его не выберет никогда.
Задача 7. Анализ вероятностной характеристики проекта.
Дано:

Цель:
1. Определите ожидаемую прибыль Х+
2. Определить риск убытков X-
3. Определить ожидаемый эффект проекта X
Решение:
1. Ожидаемая прибыль определяется по формуле:

2. Ожидаемый риск убытков определяется по формуле:

3. Ожидаемый эффект проекта X(рентабельность) определяется по формуле:
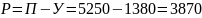
Задача 8. Выбор варианта в условиях неопределенности.
Дано:

Цель:
1. Выбрать наилучший вариант с позиции восторженного оптимиста
2. Выбрать наилучший вариант с позиции убежденного пессимиста (принцип МИНИМАКСА)
3. Выбрать наилучший вариант с позиции осмотрительного оптимиста (критерий Вальда)
Решение:
1. Наилучший вариант с позиции восторженного оптимиста – это вариант Z (+21000)
2. Наилучший вариант с позиции убежденного пессимиста (принцип МИНИМАКСА) – это вариант X (-3000)
3. Наилучший вариант с позиции осмотрительного оптимиста (критерий Вальда) определяется по формуле:

Где
K
– выбирается в меру своего оптимизма
(0 ≤ К ≤ 1),


