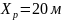Задача 1. Поиск наилучшего решения методом перебора вариантов.

Дано: Координаты потребителей и размеры судового помещения представлены в таблице.

№	X(м)	Y(м)	Z(м)	L(м)	B(м)	H(м)
1	1	4	2	32	16	12
2	30	8	2
3	13	3	6
4	25	11	6
5	4	12	8
6	30	2	10
7	20	15	10

Цель: Найти вариант установки распределителя, обеспечивающий минимальную суммарную длину коммуникаций. Точность определения координат распределителя – 0,1 м. (по всем координатам).

Решение: Задача решается методом перебора.

Недостатком метода перебора является большое количество процедур определения числовых значений критериев оптимизации.

По этой причине трехмерную задачу сводят к 3 одномерным задачам.

Тем не менее, движение к оптимуму можно еще ускорить, если применить специальные методы, предусматривающие минимизацию числа процедур при поиске оптимума, а именно использовать метод половинного деления.

Идея метода заключается в том, что оптимизация выполняется рядом последовательных дискретных этапов:

− весь диапазон изменения параметра делят пополам;

− в каждой из половин определяют среднюю точку и вычисляют или экспериментально определяют для этих точек значения критерия оптимизации;

− ту половину, в середине которой значение критерия оказалось хуже, отбрасывают, уменьшая, таким образом, ширину зоны поиска в 2 раза.

Процедуры деления повторяют до тех пор, пока ширина зоны поиска не станет меньше заданной точности оптимизации.

Что и применим для решения этой задачи.

I. Найдем минимальное значение

Для этого длину судового помещения L=0 32 м делим пополам, и в каждой из половинок находим среднюю точку и определяем значение

В первой половине 0 16 средняя точка =8, тогда равно:

Во второй половине 16 32 средняя точка =24, тогда равно:

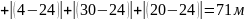
Первую половину отбрасываем, так как значение критерия оптимизации оказалось хуже, чем во второй половине.

Длину судового помещения L=16 32 м делим пополам, и в каждой из половинок находим среднюю точку и определяем значение

В первой половине 16 24 средняя точка =20, тогда :

Во второй половине 24 32 средняя точка =28, тогда :

Вторую половину отбрасываем, так как значение критерия оптимизации оказалось хуже, чем в первой половине.

Длину судового помещения L=16 24 м делим пополам, и в каждой из половинок находим среднюю точку и определяем значение

В первой половине 16 20 средняя точка =18, тогда :

Во второй половине 20 24 средняя точка =22, тогда :

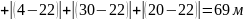
Значение критерия оптимизации в обеих половинок оказалось одинаково, следовательно, для получения оптимального критерия оптимизации необходимо использовать метод перебора.

Методом перебора значений , было установлено чтобы получить минимальное значение , необходимо чтобы значение