§4.5 Кристалдардың жылу сыйымдылығы (Классикалық теория бойынша)

Дюленг-Пти (ХІХғ.) қатты дененің жылу сыйымдылығын қарастырып: қалыпты жағдайда бір атомды кристалдардың жылу сыйымдылығы дейін артып, одан соң температура қанша артса да өзгермей тұрақты болып қалатындығын анықтады. Ал эксперимент бойынша қарастырғанда температураның кемуіне байланысты жылу сыйымдылықтың кеміп, төменгі температурада шұғыл кемитіндігін, ал температура абсолют нөлге жақындағанда жәй металдарда жылу сыйымдылық температураға пропорционал болады. Ал диэлектрик кристалдарында абсолют нөлге жақындағанда пропорционал болады.

Қатты дененің жылу сыйымдылығын түсіндіру үшін бірнеше моделдер ұсынылды, оның ең қарапайымы классикалық теория, ол Дюленг-Пти заңына тура келеді. Классикалық теория бойынша, атом кристалдық решетканың түйінінде тербеледі, оған квазисерпімді күш әсер етеді де, ол сол түйін төңірегінде тербеледі.

Кристалдағы бірнеше атомдар тобы қатты денені құрайды. Мұндай жағдайда қатты денені жинақтайтын классикалық осцилляторлар ретінде алуға болады, оның бір моліндегі саны Авогадра санына тең. Классикалық теория бойынша әрбір еркіндік дәрежеде энергия бірқалыпты таралады, олай болса бір моль кристалға келетін ішкі энергия

Классикалық теория бойынша металдардың жылу сыйымдылығы диэлектиктерге қарағанда біршама артық, өйткені металдардың электрондық өткізгіштік қабілеті болады.

Металдар үшін Дюленг-Пти заңдылығы біршама орындалғанымен, бұл модель жылу сыйымдылықтың температураға байланыстылығын толық түсіндіруге келмейді. Өте төменгі температурады диэлектрикпен металдардың жылу сыйымдылығында айырмашылық болады. Мысалы: алмаз, берилий, бор, кремний және алюминийдің бөлмелік температурадағы жылу сыиымдылығы 3R-ден біршама аз болады, ал жоғарғы температурада 3R-ге жуықтайды. Олай болса жылу сыйымдылықтың температураға байланыстылығын толық түсіндіруді кванттық теория қарастырады.

§4.6 Кристалдардың жылу сыйымдылығын Эйнштейн моделі бойынша түсіндіру

Металл кристалының жылу сыйымдылығының температураға байланыстылығын түсіндіру үшін, Эйнштейн қарапайым модель ұсынды. Сол моделге байланысты әрбір атомды осциллятор деп қарастырсақ, онда кристалдың барлық атомдары бірдей жиілікте тербеледі. Оның классикалық моделден айырмашылығы, энергиясы тек дисрет мәндерге ие болады. Мұндағы - осциллятордың тербеліс жиілігі. Бір өлшемді кванттық осциллятордың Т- температурадағы орташа энергиясы:

(4.6.1)

Кристалдағы осцилляторды үш өлшемді деп санап бір моль заттың кристалдағы ішкі энергиясы

(4.6.2)

Осы формуланы дифференциалдау арқылы қатты дененің жылу сыйымдылығын Эйнштейнше анықтасақ, онда

(4.6.3)

мұндағы -зат осцилляторының қасиеттері арқылы анықталады. (4.6.3) формуласынан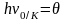 деп алсақ, онда

(4.6.4)

мұндағы - Эйнштейн температурасы деп аталады. Егер болса, онда жылу сыйымдылық 3R- ге ұмтылады. Көптеген қатты денелерде Эйнштейн температурасы (Ө) 100 К аралығында жатады. Егер Ө-ның мәні деп алсақ, онда осцилятордың тербеліс жиілігі -ке тең болады. Өте төменгі температурада -нөлге ұмтылады.

Эйнштейн теориясы бойынша алынған эксперименттік және теориялық мәндер бойынша алынған жылу сыйымдылықтың температураға байланыстылығы диэлектриктер үшінде дәл келеді, әсіресе төменгі температурадағы мөлшері дәл келеді.