
- •III тарау. Кванттық механиканың негізгі ұғымдары
- •§3.1 Шредингер теңдеуі. Толқындық функция және оның физикалық мағынасы
- •§3.2 Потенциалдық шұңқырдағы бөлшек
- •§3.3 Сызықты гармониялық осциллятор және оның энергиясының квантталуы
- •§3.4 Кеңістік квантталу. Электрон спині. Штерн- Герлах тәжірибесі
- •§3.5 Зееман− эффектісі
- •§3.6 Штарк эффектісі
- •§3.7 Паули принципі. Электрондық қабаттар
- •Атомдар ішінде электрондардың таралып орналасуы
- •§3.8 Магниттік резонанс
- •§3.9 Мозли заңы
- •Есеп шығару үлгісі
- •Білімгерлердің өздік жаттығу есептері
- •Тест сұрақтары
§3.3 Сызықты гармониялық осциллятор және оның энергиясының квантталуы
Х осінің бойындағы, массасы m бөлшекке, f=-kx квазисерпімді күш әсер етсін, мұндағы k-серіппенің қатаңдығы, х-тепе-теңдіктен ауытқу шамасы. Ондай бөлшек барлық уақытта бастапқы тепе-теңдік қалпына қарай ұмтылады. Осындай тербелмелі жүйе сызықты гармониялық осциллятор деп аталады. Осылайша электр өрісінің әсерінен тербеліске келген электронды дасызықты гармониялық осциллятор деп қарастыруға болады. Электронға өріс тарапынан әсер ететін күш, оның тепе-теңдік қалпынан ауытқуының бірінші дәрежесіне (х) пропорционал болу керек, сонда ғана сызықты гармониялық осциллятор деп қарастыра аламыз.
Бөлшекке квазисерпімді күш х-координаты бағытымен әсер етсе,
онда
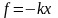 (3.3.1)
(3.3.1)
мұндай бөлшектің потенциалдық энергиясы
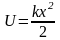 (3.3.2)
(3.3.2)
Классикалық гармониялық осциллятордың меншікті жилігін ω0, қатаңдық (k) коэффициенті арқылы тауып, оны (3.3.2) формулаға қойсақ, онда
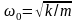 (3.3.3)
(3.3.3)
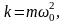
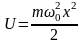 (3.3.4)
(3.3.4)
олай болса гармониялық осциллятор үшін Шредингер теңдеуін мынадай түрде жазамыз.
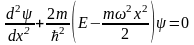 (3.3.5)
(3.3.5)
немесе
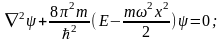
мұндағы Е - осциллятордың толық энергиясы. Бұл теңдеу арқылы энергияның (Еn) дискретті мәндері анықталады:
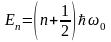 n=0,1,2…
(3.3.6)
n=0,1,2…
(3.3.6)
мұндағы, n-тербелмелі кванттық сан деп аталады.
Сонымен
осциллятордың толқындық теңдеуін
қанағаттандыратын Ψ функциясы, осциллятор
энергиясының дискреттік мәнін
қанағаттандырады. (3.3.6)формуладағы
сызықты гармониялық осциллятордың
кванттық саны әр кезде «жартылай бүтін»
кванттық санмен сиппатталады.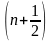 .
.
Егер n=0 болса да, осциллятор энергиясы нөлге айналмайды
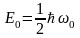 (3.3.7)
(3.3.7)
Бұл (3.3.7) теңдеу «нөлдік энергия» деп аталады.

3.2-сурет
Бұлай аталу себебі температура абсолют нөлге тең болса да, энергия нөлге теңелмейді (3.2-суреттегідей). Яғни температура абсолют нөл болған күйдің өзінде де осциллятор тербелісте болады да, ол кесіндінің кезкелген бөлігінде немесе кесінді сыртында да кездесу ықтималдығы болады, оның амплитудасынан екі еселенген мәнге үлкен болады.
§3.4 Кеңістік квантталу. Электрон спині. Штерн- Герлах тәжірибесі
Затты сыртқы магнит өрісінде зерттегенде, атомдар мен молекулалардың магнит моменттері болатындығы байқалды. Бұл атомдарда магниттік әсерлесу болатынын және атом ішіндегі электрондарда да магниттік әсерлесулер болатынын көрсетеді.
Штерн-Герлах тәжірибесінде атомның және электронның магниттік моменттері бар екендігін дәлелдеді. Олар тәжірибеде күміс атомдарының шоғын біртекті емес магнит өрісінен өткізу арқылы зерттеді. Осыған қысқаша тоқталайық.

3.3-сурет
Пеш саңылауынан шыққан атомдар шоғын вакуум түтігінің ішіндегі магнит полюстерінен (Nжәне S) өткізгенде (3.3-сурет), атомның магниттік моменті болса, оған сыртқы магнит өрісі бағыты бойынша бұруға тырысатын күш әсер етеді. Егер, өріс біртекті болмаса, онда әрбір атомға ығыстырушы күш әсер етеді, ол
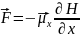 (3.4.1)
(3.4.1)
мұндағы
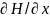 -өріс
градиенті, ол өрістің х-бағытында
біртекті емес екендігін сипаттайды.
-өріс
градиенті, ол өрістің х-бағытында
біртекті емес екендігін сипаттайды.
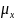 -
магниттік моменттің х-осіне түсірілген
проекциясы. Егер, атомдардың магниттік
моменттерінің бағыттары өрістің
бағытымен салыстырғанда әртүрлі болса,
онда әрбір атом түрліше ығысады.
Штерн-Герлах осылай біртекті емес магнит
өрісінен сутегі атомдарының күмістің,
сілтілік металдардың шоқтарын өткізгенде,
олардың шоқтарының әрқайсысы екі шоққа
жіктелетіндігі байқалды.
-
магниттік моменттің х-осіне түсірілген
проекциясы. Егер, атомдардың магниттік
моменттерінің бағыттары өрістің
бағытымен салыстырғанда әртүрлі болса,
онда әрбір атом түрліше ығысады.
Штерн-Герлах осылай біртекті емес магнит
өрісінен сутегі атомдарының күмістің,
сілтілік металдардың шоқтарын өткізгенде,
олардың шоқтарының әрқайсысы екі шоққа
жіктелетіндігі байқалды.
Штерн-Герлах тәжірибесінде атомның магниттік моменттерінің бағыттары өріспен бағыттас не оған қарама-қарсы болуға тиісті. Сонда ғана атомдардың шоғына сыртқы магнит өрісі әсер етіп, екіге жіктеледі. Штерн-Герлах тәжірибесінің нәтижесінде алынған атомның магниттік моменті мынадай екі себептен пайда болады:
1) электрондардың орбита бойымен қозғалуынан.
Классикалық электродинамика тұрғысынан қарағанда тұйық орбита бойымен қозғалған электрон, тұйық сыммен жүрген электр тогына ұқсас, оның магниттік моменті болады. Осылай ядроны айнала қозғалған электронның орбиталдық магниттік моментінің шамасы (μl), электронның орбиталық импульс моментіне пропорционал. СИ-жүйесінде бұл мынаған тең:
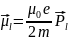 (3.4.2)
(3.4.2)
мұндағы:
μ0-вакуумдегі
магниттік өтімділік
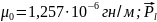 - орбиталдық импульс моменті, ол
- орбиталдық импульс моменті, ол
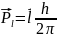 (3.4.3)
(3.4.3)
Ал, кванттық теория бойынша
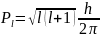 (3.4.4)
(3.4.4)
(3.4.3) →(3.4.2)теңдеуіне апарып қойсақ, онда
 (3.4.5)
(3.4.5)
мұндағы
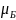 -
Бор магнетоны деп аталады.
=1,15∙10-29в.с.м.
l=0;1;2;3;.....(n-1) мәндерге ие болады.
-
Бор магнетоны деп аталады.
=1,15∙10-29в.с.м.
l=0;1;2;3;.....(n-1) мәндерге ие болады.
Егер сыртқы магнит өрісінің әсерінен, электронның магниттік моменттері, дискрет мәнге ие болса, мұндай құбылысты кеңістіктік квантталу деп атаймыз.
2) Электрон тек орбита бойымен ғана қозғалып қоймайды, сонымен қатар өзінің меншікті осінен де айналады, сондықтанда электронның меншікті магниттік моменті (μS)-болады, ол спиндік магниттік моменті деп аталады. Атом ішіндегі электронның меншікті импульс моменті мен спиндік магниттік моменті өзара байланысты. Тәжірибе нәтижелеріне қарағанда бұл екеуінің байланысы мынадай болады:
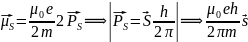 (3.4.6)
(3.4.6)
мұндағы
S-спиндік кванттық сан;
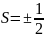 тең,
онда
тең,
онда
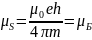 (3.4.7)
(3.4.7)
Олай болса электронның спиндік магниттік моменті жуықтап алғанда Бордың бір магнетонына тең болады. Кванттық механикада электронның спиндік импульс моменті
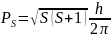 (3.4.8)
(3.4.8)
Бұл электронның меншікті импульс моменті. Осы (3.4.8) формуланы (3.4.6) формулаға қойсақ, онда
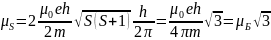 (3.4.9)
(3.4.9)
мұндағы
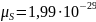 в.с.м.
болады.
в.с.м.
болады.
Магнит өрісінің бағытына түсірілген, электронның меншікті импульс моментінің проекциясы:
 (3.4.10)
(3.4.10)
мұндағы: mS- спиндік магниттік кванттық сан.
Кванттық механика бойынша электронның орбиталдық импульс моментімен спиндік импульс моменттерінің геометриялық қосындысы, электронның толық импульс моментін береді:
 (3.4.11)
(3.4.11)
егер l±S=j деп алсақ
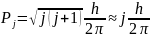 (3.4.12)
(3.4.12)
мұндағы j- ішкі кванттық сан.
Электронның толық магниттік моменті, электронның орбиталдық және спиндік магниттік моменттерінің векторлық қосындысына тең:
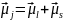 (3.4.13)
(3.4.13)
Сонымен атомның магниттік қасиеттері оның құрамындағы электрондардың магниттік моменттерімен сипатталады.
Егер атомның электрондары бірнеше болса, онда оның магниттік әсерлесулерінің жеке магниттік моменттері жинақталып қорытқы моментті береді. Онда әртүрлі типті әсерлесулер пайда болады: а) бірінші типтегі магниттік нормаль байланыс немесе L-S байланыс орындалады, яғни орбиталдық моменттерін жеке, спиндік моменттерін жеке жинақтап қосып, атомның қорытқы моменттерін табамыз:
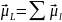 ;
;
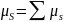 ;
;
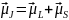 (3.4.14)
(3.4.14)
б) екінші әсерлесу типі
J-байланыс, мұнда жеке электрондардың орбиталдық және спиндік моменттерін өзара байланыстырып жалпы моментін (J) және жеке электронның толық моментін тауып, оларды қосып атомның толық моментін (J) табамыз:
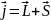 ;
;
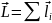 ;
;
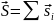 ;
;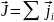
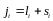
мұндағы:
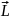 -
атомның орбиталды моменті;
-
атомның орбиталды моменті;
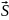 -
атомның спиндік моменті; ;
-
атомның спиндік моменті; ;
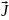 -
атомның толық моменті. Сонда кванттық
теория бойынша
-
атомның толық моменті. Сонда кванттық
теория бойынша
 (3.4.15)
(3.4.15)
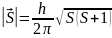 (3.4.16)
(3.4.16)
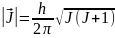 (3.4.17)
(3.4.17)
;
және
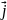 моменттердің квантталуының элементар
ережесі, атомның векторлық моделінің
сәйкестенуі мынадай түрде жазылады:
моменттердің квантталуының элементар
ережесі, атомның векторлық моделінің
сәйкестенуі мынадай түрде жазылады:
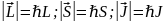 (3.4.18)
(3.4.18)
Онда әсерлесу энергиясыда: L,S,J -сандарының функциясы болады, ол жалпы түрде мынадай түрде жазылады:
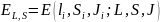 (3.4.19)
(3.4.19)
Бұл өрнек берілген L және S сандарының мәндеріне J-дің сан мәні байланысты болады: L+ S; L+ S-1; L+S-2... L-S+1; L - S; Бұл санның толық мәні: егер L> S болса, М=2S+1мәні болады, егер L<S болса, онда М=2L+1мәнге ие болады.
М-саны,
деңгейшелердің санын анықтайды, спинге
байланысты - орбиталдық магниттік
әсерлесу, ол мультиплеттік энергия
деңгейі деп аталады. Егер
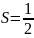 болса, М=2 дублет деп, егер S=1 болса, онда
М=3 - бұл триплет деп, ал S=0 болса М=1
сингулет деп аталады. Мультиплеттікті
екі валентті атомдардан (гелий, берилий,
магний) т.б. алынады.
болса, М=2 дублет деп, егер S=1 болса, онда
М=3 - бұл триплет деп, ал S=0 болса М=1
сингулет деп аталады. Мультиплеттікті
екі валентті атомдардан (гелий, берилий,
магний) т.б. алынады.
Өте күрделі атомдардан бұдан да бай мультиплеттік алынады.
