III тарау. Кванттық механиканың негізгі ұғымдары
§3.1 Шредингер теңдеуі. Толқындық функция және оның физикалық мағынасы
Біз
электронның корпускулалық қасиеті бар
екендігін, яғни ол масса, энергия, импульс
моменті, сызықты өлшемімен және т.б.
қасиеттерімен сипатталатындығын
білеміз. Сонымен қатар көптеген
эксперименттік фактілер бойынша,
электрон тек корпускулалық қасиетке
ғана ие болып қоймайды, оның толқындық
қасиеті де болатындығы анықталған
болатын (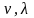
).
Толқындық (кванттық) механикада
электронның қозғалысына байланысты
толқындық қозғалыс қарастырылады. Ол
қозғалыс
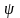- толқындық функциямен сипатталады,
сонда бұл функция кеңістіктің әрбір
нүктесінде уақытқа байланысты жазық
монохроматты толқын түрінде сипатталады:
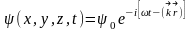(3.1.1)
мұндағы,
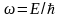немесе
;
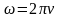ал
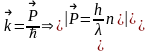(3.1.2)
мұндағы
-
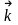толқындық вектор, Е- бөлшектің стационар
өрісте тұрақты болып қалатын толық
энергия,
-
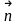толқын бетіне тұрғызылған нормаль.
(3.1.1)
формуладағы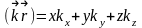
.
мұндағы
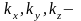координаталар бойынша толқындық
векторлар компоненттері, олар
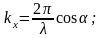
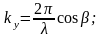
(3.1.3)
мұндағы
-
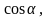
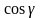толқын бетіне нормаль бойымен бағыттаушы
косинустар.
Ал
толқындық функцияның градиенті векторлық
шама, олай болса: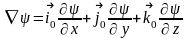
және оған Лаплас операторын қолдансақ, онда
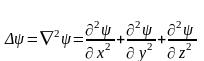
мұндағы
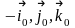координат
остері бойымен алынған бірлік векторлар.
Онда
(3.1.1) жазық монохрамат толқынның, уақыт
бойынша өзгерісі:
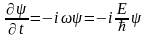(3.1.4)
ал координат бойынша өзгерісі:
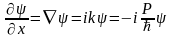(3.1.5)
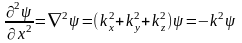(3.1.6)
немесе
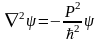(3.1.7)
Энергияның сақталу заңы бойынша:
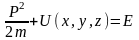(3.1.8)
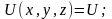
Теңдіктің
бірінші бөлігі кинетикалық энергияны
береді. Егер бөлшек тұрақты импульспен
қозғалса, онда
болады.(3.1.8) формуладан
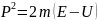(3.1.9)
(3.1.9) формуланы (3.1.7) формулаға қойсақ
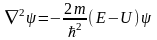
немесе
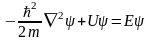(3.1.10)
(3.1.4) формула бойынша
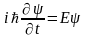(3.1.11)
(3.1.11) теңдеу, Шредингердің дифференциалдық теңдеуі деп аталады. Бұл микроәлемдегі сипатталатын негізгі кванттық механика процесі. Мұның шешуі атом энергиясының деңгейін, оған сәйкес келетін кванттық сандарды және сәулелену процесінде оның таралу облысындағы ерекше проблемеларды шешеді. (3.1.10) теңдік Шредингердің стационар теңдеуі деп аталады. Бұл теңдеу толқынның амплитудасы уақытқа тәуелді болмаған процесс кезінде қолданылады.
Егер толқындық функцияның амплитудасы уақытқа тәуелді болса, онда (3.1.10) және (3.1.11) теңдеулерді теңестіре отырып мынадай түрге келтіреміз:
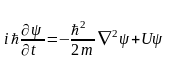(3.1.12)
Бұл теңдеу Шредингердің уақытқа тәуелді теңдеуі деп аталады. Яғни потенциалдық өрісте қозғалған бөлшектің уақытқа тәуелділігі болған жағдайда қолданады. Немесе кванттық жүйе күйінің уақыт бойынша өзгеретін есептерді шешеді. Шредингердің толқындық теңдеуі микрожүйенің орнықты күйінің әртүрлі нақты жағдайдағы энергиясын табуға мүмкіндік береді.
Шредингер теңдеуі электронның орбита бойымен қозғалуымен қатар, толқындық функция арқылы сипатталатын толқынның таралуын қарастырады. Толқындық функция электронның күйін сипаттайтын физикалық шарттың нақты түрін көрсетеді. Шредингер теңдеуі арқылы теңдеудің меншікті мәндерін және меншікті функцияларын табуға болады.
Толқындық теория бойынша жарықтың интенсивтігі берілген нүктедегі электр векторының амплитудасының квадратына пропорционал, ал корпускулалық теория бойынша бірлік беттен бірлік уақытта өткен фотондар санына (nф) пропорционал. Олай болса жарық векторының амплитудасының квадраты бірлік беттен бірлік уақытта өткен фотон санына пропорционал немесе осы беттен өту ықтималдығына пропорционал деп санауға болады.
Осылайша
қарастыру электронға қолданылса,
толқындық функцияның физикалық мағынасы:
қарастырылып отырған көлем элементі –
dV болса, онда
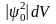- толқындық функцияның амплитудасымен
көлем элементінің көбейтіндісі,
электроның көлем элементінде болу
ықтималдығын көрсетеді. Сонда электронның
алынған көлем элементінде болу
ықтималдылығы толқындық функцияның
амплитудасының квадраты және көлем
элементіне пропорционал болады.