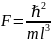§2.3 Гейзенбергтің анықталмаушылық принципі

Электронның әрі корпускулалық әрі толқындық қасиеттері бар ерекше бөлшек. Электронды макробөлшектерге тән физикалық шамалармен тек жуықтап қана сипаттауға болады, электрон кәдімгі классикалық бөлшек емес.

Классикалық механикада кез келген бөлшек белгілі траектория бойымен қозғалады, сондықтан кез келген уақыт мезетінде координаты мен импульсі дәл анықтауға болады. Микро бөлшектердің толқындық қасиеттері болатындықтан олардың классикалық бөлшектерден біршама өзгешелігі болады. Шын мәнінде микробөлшек белгілі траектория бойымен қозғалады деуге болмайды, оның координаты мен импульсінің бір мезгілде өлшенген дәл мәндері болмайды. Мысалы, «берілген нүктедегі толқын ұзындығы» ұғымында физикалық мағына жоқ, ал импульс толқын ұзындық арқылы өрнектеледі.

Осы жағдайға байланысты толқындық механикада мынадай принцип бар: электронның орнын және импульсін бір мезгілде дәл өлшеуге болмайды немесе электронның координаталарын және жылдамдықтарын бір мезгілде дәл өлшеу мүмкін емес.

Мысалы: электронның -координатасын өлшегендегі қателік , ал осы бағыттағы жылдамдығын өлшегендегі қателік болса (2.3-сурет), онда пен көбейтіндісінің шамасы Планктың тұрақтасынан кем болмайды, яғни

немесе ,

немесе

2.3-сурет

Осы қатынастарды ең алғаш (1927 ж.) неміс физигі В.Гейзенберг ұсынған болатын, сондықтан бұлар Гейзенбергтің анықталмаушылық принципі деп аталады. Бұл қатынастан, егер координатаның мәні дәл болса (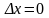 ), онда импульстың белгілі мәні болмайды ;

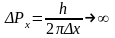Сондай-ақ болса, онда координатаның белгілі мәні болмайды

Гейзенбергтің анықталмаушылық қатынастарының өрнегінің алымындағы Планктың тұрақтасы (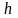 ) өте аз шама. Сондықтан координаталар мен жылдамдықтың анықталмаушылықтары тек қарапайым бөлшектерге ғана анық білінеді, макробөлшектерде байқалмайды деуге болады.

Мысалы: тозаңды (макробөлшек) алайық, оның массасы ; -координатаның қателігі болсын, сонда

Бұл жылдамдықтың анықталмаушылығы болымсыз аз шама, мұны есепке алмауға болады. Сонымен тозаңның жылдамдығы мен координатасын іс жүзінде дәл өлшеуге болады.

Енді атом ішінде қозғалған электронды қарастырайық, оның орнын анықтап көрейік. Негізгі күйдегі атомның радиусы , сондықтан атом ішіндегі электронның орны дәлдікпен анықталуы керек, яғни болуға тиіс, сонда

Ал атом ішіндегі электронның жылдамдығының өзі шамалас болады. Сонда жылдамдықты анықтаудағы қателік, сол жылдамдықтың өзіне тең. Олай болса электронның орнын және жылдамдығын бір мезгілде анықтауға болмайды. Сондықтан атомның ішінде электрон белгілі жылдамдықпен қозғалатын тұйықталған орбита бар деп айтудың өзінде еш мағына жоқ.

Атом ішіндегі электронның орнын мен жылдамдығын бір мезетте дәл анықтауға болмағанымен, оның атом ішінде берілген нүктеде болу ықтималдығын анықтауға болады. Осы ықтималдылық берілген нүктедегі электр зарядының ұзақ уақыттағы орташа тығыздығын сипаттайды.

Есеп шығару үлгісі

№1. Толқын ұзындығы 5000А⁰ фотон энергиясын, қалыпты жағдайдағы сутегі молекуласының ілгерлемелі қозғалысының энергиясымен салыстырыңдар.

Берілгені:

Табу керек: -? -?

Шешуі: Фотон энергиясы: сутегі молекуласының ілгерлемелі қозғалыс энергиясы:

есе көп. Яғни осындай көрінетін облыстағы фотон энергиясы, қалыпты жағдайдағы сутегі молекуласының ілгермелі қозғалыс энергиясынан 66 есе көп болады.

№2. Температурасы 25ºC-дегі, орташа квадраттық жылдамдықпен қозғалған альфа бөлшегінің, нейтронның және азот молекулаларының де Бройль толқын ұзындығын анықта.

Берілгені:

t=25⁰C

T=298K

Табу керек:λ_α-?

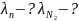
Шешуі: Орташа квадраттық жылдамдық m-бір молекуланың массасы немесе 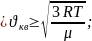µ -газдың молярлық массасы.

Де Бройль толқын ұзындығы:

Бұл орташа квадраттық жылдамдықпен қозғалған бөлшек үшін де Бройль толқын ұзындығы. ₂He⁴=(2р_m+2n_m) m_α=6,69·10^-27кг; m_n=1,675·10^-27кг;

Сонда

№3. Рентген түтікшесінің потенциал айырмасы U=40эв болып, рентген сәулесінің шекаралық толқын ұзындығы де Бройль толқын ұзындығына сәйкес келетін болса, онда де Бройль толқынына тең келетін протон, қандай кинетикалық энергияға ие болады?

Берілгені:

Табу керек:

Шешуі:

Де Бройль толқын ұзындығы:

(1)

; (2)

Рентген сәулесінің энергиясы:

(3)

(4)

Онда де Бройль толқынына тең келетін протонның кинетикалық энергиясы (сан мәнін қойсақ) ²= аДж

Жауабы:0,14 аДж.

№4. Абсцисс осінің бойымен қозғалған электронның жылдамдығының анықталмаушылығы . Бұл кездегі электронның қайда орналасқанын анықтайтын координаттың анықталмаушылығы қандай?

Берілгені:

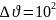м/с

Табу керек:

Шешуі: Гейзенбергтің анықталмаушылық принципі мына түрде жазылады:

(1); немесе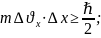 (2) энергия бойынша (3) мұндағы бөлшектің х осі бойындағы импулсь проекциясының анықталмаушылығы, -кванттық күйдегі берілген энергияның анықтамаушылығы, -осы күйдегі жүйенің келу уақыты. Олай болса (2) теңдік бойынша ;

шамасында

Жауабы: .

№5. Электрон бір өлшемді тікбұрышты қабырғалары өте биік потенциал шұңқырда орналасқан. Шұңқыр ені 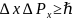формуланың көмегімен, электронның минимал энергиясы кезіндегі шұңқыр қабырғасына түсіретін қысым күшін табу керек.

Шешуі: есептің шартында , минимал энергия кезінде деп алуға болады. Сонда , ал және шұңқырдағы электронның толық энергиясы (потенциалдық энергияның нөлге тең болатынын ескерсек)

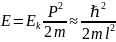(1)

Бұл шұңқырдың бір қабырғасын азғантай l шамаға жылжытайық, онда электронның осы қабырғаға түсірген F күші Е энергияның кему есебінен Fdl жұмыс атқарады деп

^dlолай болса іздеп отырған қысым күшіміз