фтт лабы для ММ / Astanin_VV

превышающих 0,2 нм (2Å), значение квадрата волновой функции настолько мало, что вероятность нахождения электрона вне сферы радиусом 0,2 нм практически равно нулю.

Рис.6. Зависимость квадрата волновой функции от расстояния для состояний 1s (а) и 2s (б).

Схематически эту картину можно представить в виде облака ве- роятностей, которое называют электронным облаком. Его плотность пропорциональна вероятности нахождения электрона в данной точке пространства, т. е. пропорциональна ψ2. Сечение электронного обла- ка можно представить в виде «фотографии», при получении которой интенсивность освещения в различных точках была пропорциональна плотности электронного облака.

На рис. 7а приведен полученный таким образом компьютерный «разрез», соответствующий электронному облаку для состояния 1s. В действительности же электронное облако трехмерно, но и волновая функция обладает сферической симметрией, поэтому любое другое центральное сечение электронного облака будет иметь такой же вид.

Вероятность нахождения электрона в данной точке сильно убы- вает с увеличением расстояния от ядра, но не обращается в ноль. Все же большая часть электронного облака сосредоточена вблизи ядра. Поэтому условно размеры электронного облака ограничивают по- верхностью, внутри которой сосредоточена определенная (например, 90 или 95 %) доля электронного заряда.

Эту граничную поверхность, характеризующую приближенно форму электронного облака, называют атомной орбиталью. Следует, однако, отметить, что форма электронного облака не совпадает с формой орбитали. Электронное облако – это облако вероятностей, не имеющее четких границ.

23

Рис. 7. «Разрез» электронных облаков для состояний 1s (a) и 2s (б)

Величина ψ2 характеризует вероятность нахождения электрона в элементе объема на расстоянии r в одном определенном направлении. Чтобы оценить, насколько часто электрон находится на расстоянии r от ядра, надо найти вероятность Р(r) пребывания электрона в шаро- вом слое между сферами радиусами r и r+dr соответственно. Соглас- но определению волновой функции эта вероятность будет равна про- изведению квадрата волновой функции на объем шарового слоя:

поскольку во всех точках шарового слоя при бесконечно малой его толщине значение квадрата волновой функции будет одно и то же.

Так как объем шарового слоя равен 4πr2dr, то

P(r) = 4πr2ψ2dr = U(r)dr,

где введенная новая функция U(r) определяется как величина, про- изведение которой на толщину шарового слоя дает вероятность пре- бывания электрона в шаровом слое на расстоянии r от центра атома.

Для состояния 1s функция U(r) имеет следующий вид:

Методами математического анализа можно легко показать, что в точке r=0 функция (22) имеет минимум, а в точке r = а – максимум. График этой функции показан на рис. 8, а.

24

Рис. 8. Функция U(r) для состояний 1s (а) и 2s (б)

Таким образом, строение атома водорода в соответствии с волно- вой теорией представляется совершенно иным, чем по теории Бора, согласно которой электрон вращается по орбите строго определенно- го радиуса и, следовательно, всегда находится на одном и том же рас- стоянии от ядра. Согласно волновой теории электрон может нахо- диться, с некоторой вероятностью, в любой точке пространства во- круг ядра. Однако на очень близких расстояниях от ядра электрон бывает сравнительно редко, так же как и на очень больших расстоя- ниях от него. Все же электрон может находиться с достаточно боль- шой вероятностью в довольно большом объеме пространства от r = 0,2Å до r = 1,5Å. Интересно отметить, что величина а, равная 0,529Å, почти точно совпадает с радиусом первой боровской орбиты, равным 0,528Å. Таким образом, понятие орбиты в волновой механике заменяется геометрическим местом точек, отвечающих наибольшей вероятности нахождения электрона в шаровом слое. Это представле- ние весьма важно для понимания процессов взаимодействия атомов при их сближении. Поскольку орбита не имеет четкой границы, то контакт двух атомов нельзя рассматривать как соприкосновение двух жестких сфер. Взаимодействие атомов может происходить в доста- точно широком интервале расстояний между ними.

Чтобы пояснить, почему электрон вероятнее всего находится на расстоянии а от ядра, в то время как величина ψ2 наибольшая в цен- тре ядра, рассмотрим некоторую аналогию. Допустим, что мы имеем шар переменной плотности. Пусть плотность этого шара будет наибольшая в центре, а по направлению к поверхности уменьшается по тому же закону, что и волновая функция. В этой аналогии квадрат волновой функции ψ2 соответствует плотности шара, а функция U(r)

25

соответствует массе шарового слоя толщиной dr, находящегося на расстоянии r от центра шара.

При принятой зависимости плотности шара от расстояния масса шарового слоя вблизи центра шара будет много меньше, чем масса шарового слоя на расстоянии а, поскольку объем шарового слоя на расстоянии а во много раз больше объема шарового слоя вблизи цен- тра. В итоге общая масса шара будет, в основном, определяться плот- ностью вблизи точки а.

Волновая функция для состояния 2s также является сферически симметричной. На рис. 6,б показано изменение квадрата волновой

функции с расстоянием. Квадрат волновой функции

наибольшее значение в центре атома, при r=2а проходит через нуль, а в точке r = 4а принимает максимальное значение. При еще большем удалении от центра ядра волновая функция и ее квадрат резко уменьшаются по абсолютной величине и на расстоянии 6 Å от центра атома практически обращаются в нуль. Таким образом, вероятность нахождения электрона в состоянии 2s максимальна в двух точках: в центре атома и на расстоянии от него, равном 4а.

Для наглядности картину атома водорода для состояния 2s тоже представляют в виде электронного облака, плотность которого в каж-

дой точке пропорциональна квадрату волновой функции ψ22s . На

рис. 7,б схематически изображено электронное облако для состояния 2s, полученное таким же способом, как и для состояния 1s, а именно: сечение электронного облака показано в виде фотографии, при полу- чении которой интенсивность освещения в разных точках была про- порциональна ψ22s . Размеры электронного облака для состояния 2s в 5 раз больше размеров электронного облака для состояния 1s, а плот- ность электронного облака для состояния 2s в каждой точке пример- но в 50 раз меньше, чем для состояния 1s.

Вероятность пребывания электрона в шаровом слое на различных расстояниях от центра атома для состояния 2s приведена на рис. 8, б в виде функции U(r). Функция U(r) для состояния 2s имеет два макси- мума: при r = а и r = 4а. Максимальное значение функции U(r) в точ- ке r = 4а в несколько раз больше максимума в точке r = a, и, следова- тельно, электрон в состоянии 2s больше всего пребывает на расстоя- нии 4а от центра атома. Это расстояние соответствует второй боров- ской орбите. Однако, в отличие от теории Бора, согласно волновой

26

механике электрон с достаточно большой вероятностью может нахо- диться в довольно широкой области пространства, в том числе и на орбите, соответствующей 1s состоянию, хотя вероятность этого срав- нительно мала.

Для более высоких s-состояний (3s, 4s и т. д.) наблюдаются сле- дующие общие закономерности.

1.Волновые функции для s-состояний а, следовательно, и квад- раты волновых функций и функция U(r) сферически симметричны.

2.Чем больше главное квантовое число п, тем более «размыто» электронное облако, тем на большие расстояния оно рас- пространяется от центра и плотность электронного облака в со- ответствующих точках становится все меньше.

3.Функция U(r) имеет п максимумов, причем наибольшим по ве- личине будет n-й максимум от центра, т. е. электрон в состоянии ns наибольшее время пребывает в области пространства, которой соот- ветствует n-й максимум функции U(r). Следовательно, чем больше главное квантовое число п, тем на большем расстоянии от ядра чаще всего бывает электрон в этом состоянии. Электрон может быть и в любой другой точке пространства, но вероятность этого мала.

Рассмотрим теперь p-состояния атома водорода. Состояние 2р соответствует следующим значениям квантовых чисел: п = 2 и p = 1. Для этого состояния третье квантовое число принимает три значения:

ml = 1; 0; +1, и в соответствии с этим состояние 2р описывается тремя волновыми функциями:

В этом случае волновые функции уже не являются сферическими симметричными и зависят от всех трех координат r,ϕ и θ.

Чтобы наглядно представить распределение электронной плотно- сти в атоме водорода в 2p-состоянии, используют возможность раз- ложения волновой функции на три сомножителя (см. уравнение 12):

27

ψ 2 = R 2Θ2Φ 2 .

Для описания электрона в каком-либо состоянии рассматривают отдельно квадрат первого члена R2, который называют радиальным вероятностным множителем или радиальной функцией, и отдельно квадрат произведения двух остальных функций, зависящих только от направления и не зависящих от расстояния. Значения второго члена (ΘΦ)2 представляют в виде так называемой полярной диаграммы. Для построения полярной диаграммы из начала координат проводят пря- мую в направлении, определяемом углами θ и φ, и на этой прямой от- кладывают отрезок, равный по величине функции (ΘΦ)2. Геометриче- ское место точек, соответствующих концам этих отрезков, и пред- ставляет собой полярную диаграмму.

Радиальный вероятностный множитель R2 для всех трех функций ψ2pz, ψ2px и ψ2pg одинаков и равен:

График этой функции приведен на рис. 9. Радиальный множитель электронной плотности для состояния 2р в центре атома равен нулю, с увеличением расстояния от центра атома возрастает, достигает мак- симума при r=a и далее уменьшается. На расстоянии, превышающем 5Å, радиальный множитель практически равен нулю.

Остальные два множителя ΘΦ для каждого значения третьего квантового числа различны. Для третьего квантового числа ml, равно- го нулю, произведение этих функций имеет вид:

ΘΦ = cos θ .

Построим график этой функции. Предположим вначале, что φ=0; это будет плоскость z0x. Рассмотрим, каким образом изменяется функция ΘΦ в этой плоскости в зависимости от угла θ. При из- менении угла от 0 до π/2 cosθ изменяется от 1 до 0, при дальнейшем увеличении угла θ cosθ уменьшается и при θ=π становится равным

−1; далее функция ΘΦ возрастает и при θ = 23 π снова принимает зна-

чение, равное нулю. С дальнейшим увеличением угла θ функция ΘΦ продолжает возрастать, пока при θ=2π не станет равной 1. В итоге получим кривую в виде двух окружностей, причем верхняя окруж- ность соответствует положительным значениям волновой функции, а

28

нижняя – отрицательным (рис. 10, а). Функция (ΘΦ)2 отличается от ΘΦ тем, что она во всех точках положительна и образована не двумя окружностями, а двумя лепестками, вытянутыми вдоль оси z (рис. 10, б). Так как функция (ΘΦ)2 не зависит от φ, то для любой другой плос- кости, проходящей через ось z и составляющей угол φ с плоскостью z0x, получим точно такую же кривую. В итоге полярная диаграмма для состояния 2р и ml = 0 будет представлена фигурой (рис. 11), по- лученной вращением вокруг оси z приведенных на рис. 10,б лепест- ков. Полярная диаграмма для состояния 2р (ml = 0), вытянута вдоль оси z, поэтому волновую функцию для этого состояния обозначают

.

Аналогично полярные диаграммы для состояний m = +1 и –1 представляют собой такие же поверхности, как и для первого состоя- ния, но расположенные вдоль осей х и у соответственно (рис. 11, б, в). В соответствии с этим полярные диаграммы для m = + 1 и –1 обозна- чают и .

Ни радиальный множитель, ни полярная диаграмма не опре- деляют полностью вероятность нахождения электрона в окрестностях данной точки. В этом отношении не следует путать полярную диа- грамму с электронным облаком. Для того, чтобы найти вероятность нахождения электрона в окрестностях точки с координатами r1, φ1, θ1, например, в состоянии ml = +1, необходимо прежде всего найти функцию (ΘΦ)2. Для нахождения произведения (ΘΦ)2 для заданных значений φ1 и θ1 проводим прямую линию в направлении, определяе-

29

мом этими координатами, до пересечения с полярной диаграммой и находим длину отрезка 0Р (рис. 10, б), заключенного между началом координат и точкой пересечения. Далее значение радиального веро- ятностного множителя R2 умножаем на 0Р и получаем вероятность нахождения электрона в окрестностях точки с координатами r1, φ1, θ1. Плотность электронного облака в рассматриваемой точке будет про- порциональна найденной величине. Поскольку полярный множитель имеет наибольшие значения в направлении оси x, то и электронное облако будет наиболее плотным в направлении оси x.

z

Рис. 11. Полярные диаграммы атома в р-состояниях (р-орбитали)

Аналогично можно представить себе атом водорода для других состояний. Электронные облака для состояний ml = –1 и ml = 0 вытя- нуты вдоль осей y и z, как и соответствующие им полярные диаграм- мы. Обычно для простоты p-орбитали представляют в форме вытяну- тых вдоль осей лепестков.

Выше указывалось, что оси х, у и z для атома можно направить как угодно. Чтобы описание атома было более определенным, пола- гают, что атом находится в слабом магнитном поле. Вдоль этого поля и направляют ось z. Одновременно приобретают реальный физиче- ский смысл оси х и у. Внешнее магнитное поле не следует расцени- вать, как некую искусственную ситуацию - существует магнитное поле Земли, существуют магнитные поля от соседних атомов в кри- сталле и т.д. Иначе говоря, ситуацию отсутствия магнитного поля в реальности представить труднее, чем его наличие. При таких услови- ях электронные облака для всех трех p-состояний взаимно перпен- дикулярны. Именно такой случай был рассмотрен выше. Для свобод- ных атомов электронные облака для p-состояний с разным значением

30

m однотипны и неразличимы; такие состояния, как указывалось вы- ше, называют вырожденными. Существенно, что сложение трех элек- тронных облаков для ml = 0, ml = +1 и ml = –1 дает сферически сим- метричное электронное облако. Действительно

ψ22 p z + ψ22 p x + ψ22 p y = R2 (cos2 Θ + sin2 Θ cos2 ϕ + sin2 Θsin2 ϕ) = R2 .

Электронные облака для более высоких p-состояний (Зр, 4р и т. д.) сходны по общей форме с описанными выше для 2р-состояния. Они также вытянуты вдоль осей х, у и z. Отличие же состоит в сле- дующем. Для 2p-состояния вдоль любой прямой, проходящей через начало координат, плотность облака с удалением от ядра сначала возрастает, достигает максимума, а затем уменьшается. Для более высоких состояний закономерность изменения плотности электрон- ного облака от расстояния до ядра сложнее.

Поскольку для d-состояний возможны пять различных значений третьего квантового числа ml (–2; –1; 0; +1; +2), то они описываются пятью волновыми функциями

Полярные диаграммы этих функций (рис. 12) имеют более узкие и более вытянутые лепеспки, чем диаграммы p-состояний. Другая важная особенность полярных диаграмм d-состояния – это наличие четырех направлений в пространстве. Один электрон занимает две пространственные оси. Эта особенность важна для понимания направленности связей, образованных d-электронами. Причем, направления d-орбиталей могут совпадать с направлениями p- состояний, т. е. располагаться по координатным осям, но могут и от- личаться, проходя по биссектрисам координатных углов.

31

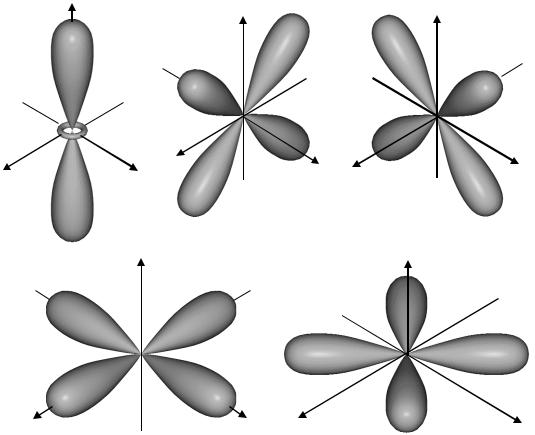
Как и для p-состояний, если сложить все электронные облака для d-состоянии с различными ml, то получится сферически симмет- ричное электронное облако.

Рис. 12. Полярные диаграммы атома водорода для d-состояний

1.3. Многоэлектронные атомы

Приведенные выше результаты справедливы для атома водорода и водородоподобных атомов, у которых в центральном потенциаль- ном поле, образованном ядром, находится один электрон. Строение многоэлектронных атомов значительно сложнее. Точного решения уравнения Шредингера для многоэлектронных атомов не получено, так как не удается точно найти потенциальную энергию подобной си- стемы.

В многоэлектронном атоме элемента с порядковым номером Z потенциальная энергия каждого электрона складывается из энергии

32